核心高强钢管混凝土组合柱轴压承载力计算新方法*

龙跃凌 蔡健

(1.香港理工大学土木及结构工程学系,香港九龙;2.华南理工大学土木工程系,广东广州 510640)

核心高强钢管混凝土组合柱(简称核心柱)是在钢管混凝土与钢骨混凝土的基础上发展而来的新型构件.它以高强钢管混凝土为核心,在其周围浇筑普通钢筋混凝土而形成.与一般钢管混凝土柱相比,核心柱的钢管表面不仅不需要做防火、防锈、防腐处理,还大大提高了钢材的耐火性能和耐久性,同时,钢管内外的混凝土可有效防止钢管内外向的局部屈曲[1-2].目前,国内外对核心柱的力学性能研究较少[1-8],仅有的研究也大多集中在方形截面核心柱的静力性能和抗震性能等方面.关于核心柱的轴压承载力计算方法主要有两种[1-4]:一是不考虑钢管以及箍筋对混凝土的约束作用,按钢骨混凝土计算,即分别计算混凝土和钢(钢管和钢筋)的承载力后将两者简单叠加;另一种是考虑钢管对混凝土的约束作用,不考虑箍筋对混凝土的约束作用,钢管及其约束混凝土按钢管混凝土计算,钢管外的混凝土按普通混凝土计算.上述两种方法均不能合理地考虑核心柱钢管内外混凝土的约束效应以及截面形状对钢管外混凝土力学性能的影响.

针对上述问题,文中在前人的研究[1-2]基础上,考虑了方形、圆形截面的核心柱钢管内外混凝土的约束效应及其差异,同时考虑截面形状对钢管外混凝土的影响,提出方形、圆形核心柱轴压承载力计算的新方法,并将该方法与现有方法进行了比较.

1 核心高强钢管混凝土组合柱的受力机理

核心高强钢管混凝土组合柱的截面如图1所示.

图1核心高强钢管混凝土组合柱中的混凝土属于约束混凝土,按约束效应的不同可以分为 3类:钢管约束混凝土、螺旋(圆形)箍筋约束混凝土以及矩形箍筋约束混凝土.其中,方形、圆形截面的核心柱钢管内的混凝土为钢管约束混凝土,钢管外的混凝土分别为矩形箍筋约束混凝土和螺旋(圆形)箍筋约束混凝土.

钢管约束混凝土、螺旋(圆形)箍筋约束混凝土以及矩形箍筋约束混凝土的约束效应大小和作用方式是不同的.其中,钢管约束混凝土的约束效应最大,且圆形钢管对混凝土的约束沿柱长度方向是连续的;螺旋(圆形)箍筋约束混凝土的约束效应次之,螺旋(圆形)箍筋对混凝土的约束沿柱长度方向是间断的;矩形箍筋约束混凝土的约束效应最小,约束效应主要在 4个角部,其对混凝土的约束沿柱长度方向是间断的.

已有研究[2]表明,方形截面试件的箍筋约束作用比较弱,仅在箍筋的转角处对混凝土有较大的约束,而且钢管外的混凝土由于受到的横向约束小,其强度也提高得不多,且不像圆形截面试件那样屈服后出现明显的强化阶段.圆形截面试件的箍筋约束作用大且均匀,所以圆形截面试件的承载力较大,延性较好.

文献[9]详尽叙述了轴压作用下核心高强钢管混凝土组合柱的受力过程,现简述如下:

第一阶段为受力初期,混凝土的横向变形很小,钢管内混凝土、钢管和外包钢筋混凝土之间的相互作用较小[9].

第二阶段,随着荷载的增加,混凝土的横向变形超过钢材的横向变形,钢管对其内混凝土的约束作用增大;钢管在约束管内混凝土的同时,其横向变形受到外包混凝土的约束,环向拉应力较一般钢管混凝土中钢管承受的拉应力小;受箍筋约束的管外混凝土处于三向受压状态,但由于钢管约束了一部分混凝土的变形,外包混凝土受到的径向压力较其在普通钢筋混凝土中的小,箍筋应变的增长相对较慢[9].

第三阶段,当纵向钢筋和钢管纵向先后屈服后,钢管的横向变形明显加快,对管外混凝土产生较大的压应力;管外混凝土受到纵向荷载和来自钢管的径向压力的作用,横向应变剧增,箍筋对钢管外混凝土的约束明显增强.钢管内约束混凝土的承载力在试件整体屈服后能继续增长;箍筋约束了钢管外混凝土的横向变形,使之处于三向受压状态,并通过外包混凝土对核心钢管混凝土产生约束作用,导致这两者的承载力和变形能力均明显提高,从而保证了在保护层混凝土部分压碎的情况下核心柱整体承载力能继续增长.当箍筋屈服时,其对钢管外混凝土的约束作用达到峰值,之后进入应力下降段,此时内核钢管混凝土仍处于应力上升阶段,核心柱的整体承载能力继续增加.当内核钢管混凝土接近其三轴强度时,其应力增长较慢,钢管外混凝土的应力下降总和超过钢管内混凝土的应力增量时,柱的承载力达到最大值,之后承载力开始进入下降段,直至钢管外混凝土被压碎,试件破坏[9].

2 核心高强钢管混凝土组合柱轴压承载力的主要计算方法

核心柱轴压承载力按钢骨混凝土计算的表达式为[4]

式中:fc为混凝土轴心抗压强度(不考虑混凝土的约束效应);Ac为混凝土总横截面面积;fyi为钢管或钢筋的屈服强度;Asi为钢管横截面积或钢筋的横截面积.

核心柱轴压承载力按钢管混凝土外包普通混凝土计算的表达式为[4]

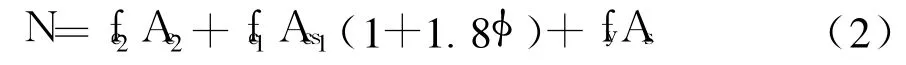
式中:fc2、Ac2分别为钢管外围混凝土轴心抗压强度和横截面积;fc1、Acs1分别为钢管内混凝土轴心抗压强度和钢管混凝土的横截面积;fy、As分别为纵向钢筋屈服强度、总横截面积;φ为钢管混凝土的套箍指标,φ=Astfay/Ac1fc1,其中fay、Ast分别为钢管屈服强度和横截面积,Ac1为钢管约束混凝土(钢管内混凝土)的横截面积.

文献[2]中考虑到外围混凝土先压溃,引入折减系数,提出核心柱轴压承载力的表达式:

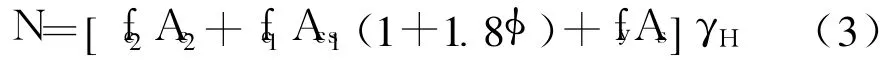
式中:γH=1.1-0.01φ-0.23k,k=dt/B,dt为钢管直径(外径),B为方形柱截面的宽度.

3 核心高强钢管混凝土组合柱轴压承载力计算新方法

3.1 圆形核心柱轴压承载力的计算方法

由以上分析可知,由于达到极限承载力前保护层混凝土已被压碎,因此忽略保护层混凝土对极限承载力的贡献.圆形核心柱轴压极限承载力由钢管、纵向钢筋、钢管约束混凝土、钢管外螺旋(圆形)箍筋约束混凝土的承载力构成,并假定在达到最大承载力时,钢管、纵向钢筋都已经屈服,故圆形核心柱轴压承载力计算公式如下:

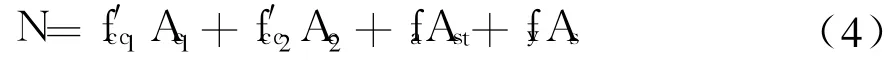
式中:f′cc1为钢管约束混凝土轴心抗压强度;f′cc2为螺旋(圆形)箍筋约束混凝土轴心抗压强度;fa为钢管纵向强度.

钢管与螺旋(圆形)箍筋的约束效应大小和作用方式是不同的,所以一般情况下 f′cc1不同于 f′cc2. Mander等[10]在研究箍筋约束混凝土时提出了等效侧向约束力的概念,并根据William-Warnke五参数混凝土多轴破坏准则给出了箍筋约束混凝土轴心抗压强度的计算公式:

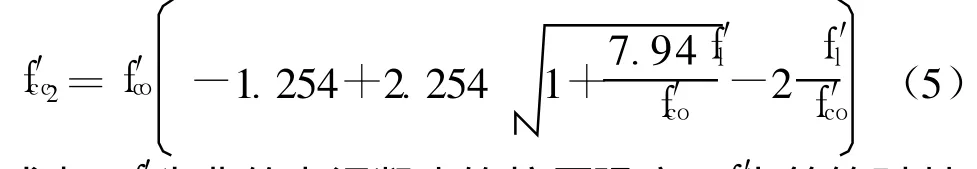
式中:f′co为非约束混凝土的抗压强度;f′l为箍筋对其约束混凝土的有效约束应力.

式中:ke为有效约束系数;fl为箍筋对其约束混凝土的约束应力.

根据文献[10],对于圆形或螺旋箍筋,ke为

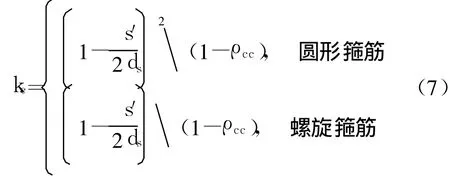
式中:ds为螺旋(圆形)箍筋直径;s′为箍筋净间距; ρcc为纵筋的配筋率.

假定核心柱达到极限承载力时箍筋屈服,且箍筋对其约束混凝土的约束应力均匀分布,如图 2所示,由力平衡可得

式中:fyh和Asp分别为箍筋屈服强度和横截面积;s为箍筋间距;fsr为箍筋的环向拉力.

由式(8)、(9)可得

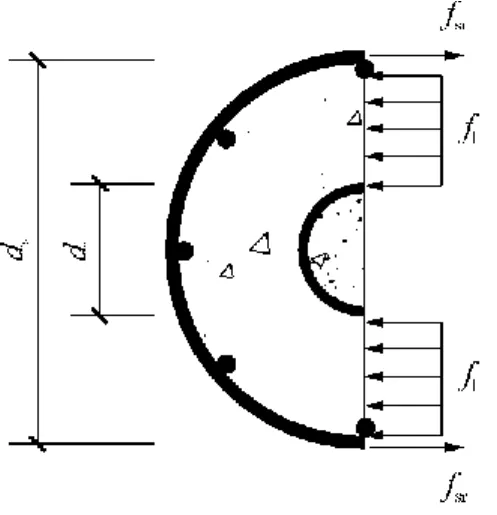
图2 圆形核心柱箍筋约束混凝土的约束应力Fig.2 Confinement stress of concrete confined by circular hoops of circu lar composite columnswith core of highstrength concrete-filled steel tube

核心柱中钢管处于比较复杂的三向受力状态,钢管侧向约束应力需考虑钢管纵向应力的影响. Sakino等[11]给出了钢管混凝土轴压柱在到达极限承载力时,钢管环向应力及纵向应力与钢管屈服强度的关系:

式中:fst为钢管环向应力.

类似地,圆形核心柱钢管约束混凝土的约束应力如图 3所示,由力平衡可得

式中:T为钢管壁厚;flt为钢管对其约束混凝土的约束应力.

图3 圆形核心柱钢管约束混凝土的约束应力Fig.3 Confinementstress of concrete confined by steel tube of circular composite columns with core of high-strength concrete-filled steel tube

由式(11)、(13)可得

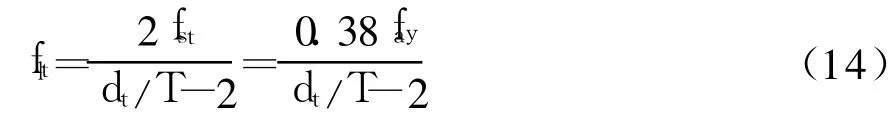
与螺旋(圆形)箍筋的约束效应不同,钢管对混凝土的约束沿柱长度方向是连续的,所以有效约束系数ke=1,即钢管对其约束混凝土的有效约束应力f′lt=flt.文献[10]给出的箍筋约束混凝土轴心抗压强度的计算公式是根据William-Warnke五参数混凝土多轴破坏准则得到的,同样适用于钢管约束混凝土,即

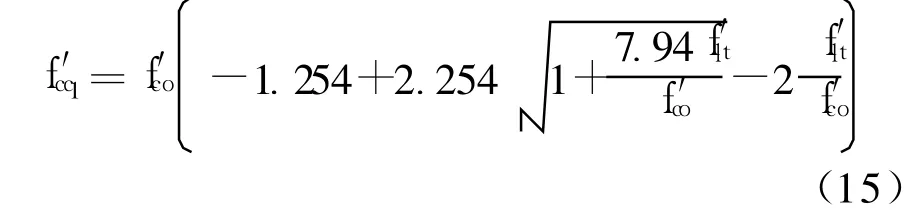
3.2 方形核心柱轴压承载力的计算方法

从前面分析可知,方形核心柱轴压承载力的表达式与圆形核心柱一样,见式(4).方形核心柱的矩形箍筋对混凝土的约束并不均匀,主要在 4个角部,所以对钢管外的混凝土的约束作用较螺旋(圆形)箍筋小.矩形箍筋混凝土的有效约束区如图 4所示.

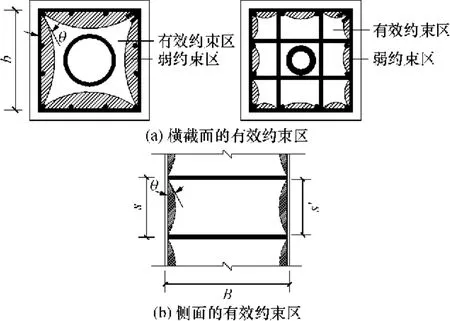
图4 方形核心柱箍筋约束混凝土的有效约束区Fig.4 Effectively-confined area of concrete con fined by square hoops of square composite columns with core of highstrength concrete-filled steel tube

借鉴 Mander等[10]的等效侧向约束力的概念,有效约束系数ke的表达式为

式中:ke1、ke2为分别为横截面有效约束系数、侧面有效约束系数.

定义ke1为混凝土有效约束区面积Ae和箍筋混凝土总截面面积Ac2之比,即

式中:Af为弱约束区总面积.

假定有效约束面的边界线为二次抛物线,约束界线边的切角为θ,如图4(a)所示.Mander等[10]建议对矩形箍筋约束混凝土,θ=45°.因此,单个弱约束区面积AI为

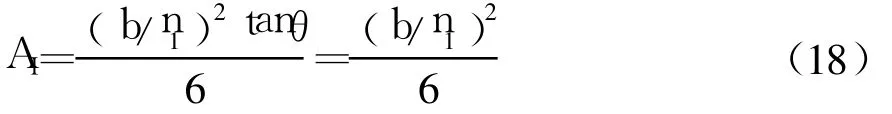
式中:n1为横截面每边被箍筋分开的段数;b为方形核心柱的截面宽度(不计保护层厚度),如图4(a)所示.

横截面弱约束区总数为m=4n1,则横截面弱约束区的总面积为

横截面有效约束区面积Ae为

由式(17)-(20)可得

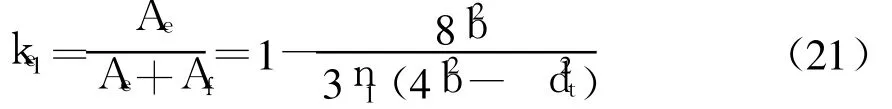
类似地,可得侧面有效约束系数ke2为

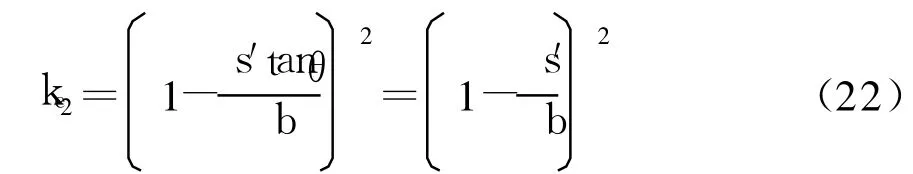
将式(21)、(22)代入式(16)可得:

假定核心柱达到极限承载力时箍筋屈服,且箍筋对其约束混凝土的约束应力均匀分布,如图 5所示,由力平衡可得

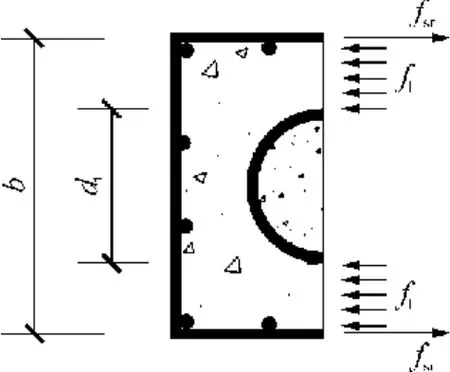
图5 方形核心柱箍筋约束混凝土的约束应力Fig.5 Confinement stress of concrete confined by square hoops of square composite columns with core of high-strength concrete-filled steel tube

由式(24)、(25)可得

将式(26)代入式(6)可得箍筋对其约束混凝土的有效约束应力f′l,从而代f′l入式(5)可得方形核心柱箍筋约束混凝土轴心抗压强度f′cc2.

方形核心柱的钢管约束混凝土强度f′cc1、钢管纵向强度fa的确定与圆形核心柱一样,这里不再赘述.

4 文中方法与现有方法的比较

采用文中方法以及式(1)-(3)分别对文献[1-2]的圆形、方形核心柱试件的轴压承载力 Nuc进行计算,结果见表1.

从表1可见,式(1)(即按钢骨混凝土计算)将核心柱的轴压承载力低估了11.5%;式(2)、(3)将核心柱的轴压承载力分别高估了14.0%和8.7%;文中方法计算值总体上与实验值最接近(略高于实验值2.6%),且文中方法计算结果的离散性较小.与式(1)-(3)相比,文中方法考虑了方形、圆形截面的核心柱钢管内外混凝土的约束效应及其差异,同时考虑了截面形状对钢管外混凝土的影响,能较为合理地评估核心钢管混凝土组合柱的轴压承载力.

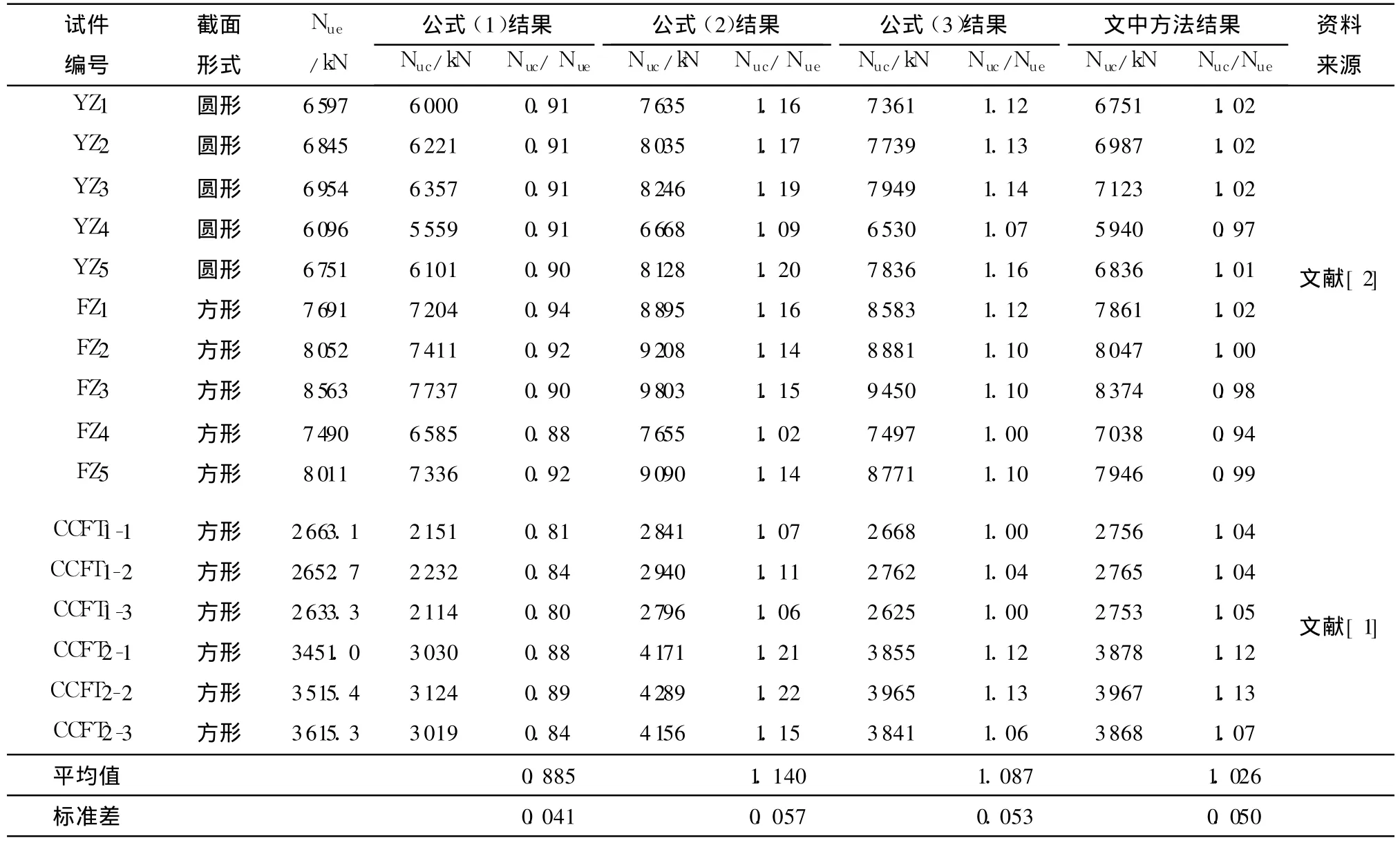
表1 轴压承载力计算值和实验值的比较Table 1 Comparison of test resu lts of axialbearing capacity with calculated values

5 结语

文中针对核心钢管混凝土组合柱钢管内混凝土与管外混凝土约束效应大小以及约束方式的不同,同时考虑圆形截面和方形截面对钢管外混凝土的影响,提出了一种核心钢管混凝土组合柱轴压承载力计算的新方法.该方法对核心钢管混凝土组合柱试件轴压承载力的计算结果与试验结果吻合良好,优于现有方法.

由于考虑了方形、圆形截面的核心柱钢管内外混凝土的约束效应及其差异,同时考虑了截面形状对钢管外混凝土的影响,因此文中方法能较为合理地评估核心钢管混凝土组合柱的轴压承载力.

[1] 聂建国,柏宇,李盛勇,等.钢管混凝土核心柱轴压组合性能分析[J].土木工程学报,2005,38(9):9-13.

Nie Jian-guo,Bai Yu,Li Sheng-yong,et al.Analysis on composite column with inside concrete filled steel tube under axial compression[J].China Civil Engineering Journal,2005,38(9):9-13.

[2] 蔡健,谢晓锋,杨春,等.核心高强钢管混凝土柱轴压性能的试验研究 [J].华南理工大学学报:自然科学版,2002,30(6):81-85.

Cai Jian,Xie Xiao-feng,Yang Chun,et al.An experimental research on the composite column with core of highstrength concrete filled steel tube underaxial compression loading[J].Journal of South China University of Technology:Natural Science Edition,2002,30(6):81-85.

[3] 幸坤涛,赵国藩,岳清瑞.高强钢管混凝土核心柱抗震性能的神经网络评估[J].工业建筑,2002,32(10): 63-65.

Xing Kun-tao,Zhao Guo-fan,Yue Qing-rui.Evaluation of seism ic properties of core column with high strength concrete filled steel tube based on artificial neural network [J].Industrial Construction,2002,32(10):63-65.

[4] 幸坤涛,赵国藩,岳清瑞.高强钢管混凝土核心柱轴压短柱的承载力研究[J].钢结构,2002,17(1):18-21.

Xing Kun-tao,Zhao Guo-fan,Yue Qing-rui.Research on bearing capacity of axial com pressed short core column with high strength concrete filled steel tube[J].Steel Structure,2002,17(1):18-21.

[5] 李惠,吴波,林立岩.钢管高强混凝土叠合柱的抗震性能研究[J].地震工程与工程振动,1998,18(1):45-52.

Li Hui,Wu Bo,Lin Li-yan.Study on seismic properties of laminated column with high strength concrete containing steel tube[J].Earthquake Engineering and Engineering Vibration,1998,18(1):45-52.

[6] 李惠,王震宇,吴波.钢管高强混凝土叠合柱抗震性能与受力机理的试验研究 [J].地震工程与工程振动, 1999,19(3):27-33.

Li Hui,Wang Zhen-yu,Wu Bo.Experimental research on mechanism and seism ic performance of laminated column with steel tube filled with high-strength concrete[J]. Earthquake Engineeringand Engineering Vibration,1999, 19(3):27-33.

[7] 钱稼茹,康洪震.钢管高强混凝土组合柱抗震性能试验研究[J].建筑结构学报,2009,30(4):85-93.

Qian Jia-ru,Kang Hong-zhen.Experimental study on seismic behavior of high-strength concrete-filled steel tube composite columns[J].Journal of Building Stuctures, 2009,30(4):85-93.

[8] 黄志辉,程丽荣,林立岩,等.钢管高强混凝土叠合柱核芯区抗剪试验研究与有限元分析 [J].工业建筑, 2001,31(7):50-53.

Huang Zhi-hui,Cheng Li-rong,Lin Li-yan,et al.Experimental study and finite elementanalysis on shear behavior of steel tube fill high-strength concrete composite column core area[J].Industrial Construction,2001,31(7):50-53.

[9] 谢晓锋.高强钢管(骨)混凝土核心柱轴压性能的试验研究[D].广州:华南理工大学建筑学院,2002.

[10]Mander JB,Priestley M JN,Park R.Theoretical stressstrain model for confined concrete[J].Journal of Structural Engineering,ASCE,1988,114(8):1804-1826.

[11]Sakino K,Nakahara H,Morino S,et al.Behaviour of centrally loaded concrete-filled steel-tube short columns[J]. Journal of structural Engineering,ASCE,2004,130(2): 180-188.