香港地区降水趋势及其演变过程分析

张润润

(河海大学水文水资源学院，江苏南京 210098)

趋势分析是研究气候变化和水文时间序列变化规律的重要途径.关于时间序列趋势显著性检验的统计方法很多，应用较为广泛的是非参数Mann-Kendall(MK)趋势检验方法[1].徐利岗等[2]利用MK趋势检验方法研究了我国北方荒漠区降水在时间、空间上的变化趋势;王志福等[3]运用MK趋势检验方法分析了我国极端降水事件的变化趋势.MK趋势检验方法是基于序列随机独立的假设，已有研究表明，忽略序列相关性，用MK趋势检验方法进行分析会导致趋势显著性的估计误差[4-7].国内许多研究在考虑序列相关性对于序列趋势分析的影响相对不足，一般直接假设序列独立而忽略序列相关性对分析结果的影响.国外在这方面的研究工作相对要完善一些，Adamowski等[8]在对年降水量极值序列进行趋势分析时，通过对序列的白化，去除序列自相关因素，然后运用MK趋势检验方法对区域降水量极值序列进行趋势分析.Khaliq等[9]考虑了序列相关性对趋势显著性的影响，运用改进的Mann-Kendall(MMK)趋势检验方法对加拿大地区的径流趋势进行研究.

趋势是变量持续变化累积形成的一种统计结果，是一段时间内变量的变化倾向.Hamed等[7]以40a为滑动窗口对德国Main River的年径流序列不同时段内的趋势进行了分析，研究发现趋势状态与分析时段关系密切，随时间的推移逐步变化.国内大量关于趋势分析方面的研究工作往往只是依据序列资料，运用相关趋势检验方法进行显著性检验之后即对序列的趋势特性(包括趋势方向、趋势显著性等)做出判断，对于序列趋势的演变过程考虑不多.

香港地区地处中国东南沿海，受控于亚热带季风气候，降水年内分布极为不均.目前，香港地区的淡水约80%通过东江—深圳(东深)供水工程供给.尽管香港地区本地集水量仅占香港地区供水量的20%，但系统了解香港地区降水特性，尤其是降水趋势，是东深供水工程实施对港弹性供水的基本前提.针对以往研究中存在的不足，本文利用MK及MMK趋势检验方法对香港地区降水趋势进行分析，对比相关性对趋势显著性的影响，并分析延伸和回溯2种时段变化模式下序列趋势的演变过程，进一步将序列趋势演变过程与其累积离差过程进行对比分析，分析趋势的形成原因与持续特性，为东江流域水资源的合理配置和香港地区供水安全提供技术支持.

1 研究方法

1.1 MK趋势检验方法

对于时间序列X={x1，x2，…，xn}，定义统计量S为[10-11]:

假设各变量独立同分布，则统计量S近似服从正态分布，其均值、方差分别为[11]:

式中:m——序列中秩次相同的组数;tj——第j组秩次相同所包含观测值的个数.

当n＞10，用式(5)来计算Mann-Kendall统计量[11]:

当样本数量n比较大时，Uc近似服从标准化正态分布.假设序列无趋势，给定显著性水平 α，则可以根据与临界值Uα/2的比较结果判定序列趋势的统计显著性.

1.2 MMK趋势检验方法

MK趋势检验方法基于序列独立性假设，序列的相关性会对Var(S)有明显影响.序列负的相关性会增大Var(S)，对于具有负相关性的序列直接用MK趋势检验方法检验将导致对序列趋势显著性的低估;反之，将导致对序列趋势显著性的高估[6-7，9].本文基于Khaliq等[9]的研究成果，选择趋势检验能力强、由Hamed等改进的MMK趋势检验方法对存在相关性的序列进行趋势检验分析[6].该方法考虑序列相关性对于Var(S)的影响，对Var(S)进行修正，具体做法如下.

对于时间序列X={x1，x2，…，xn}，首先计算基于序列秩次的趋势估计量β[12]

并从序列X={x1，x2，…，xn}中祛除该趋势项，获得与原序列相应的平稳序列{yi}ni=1:

然后，求序列{yi}ni=1对应的秩次序列，计算其自相关函数ρs(i).ρs(i)用r(i)根据式(8)估计[13]:

式中:Ri——yi的秩次;¯R——秩次的均值.最后，依据r(i)求解具有相关性序列的趋势统计量S的方差Var*(S):

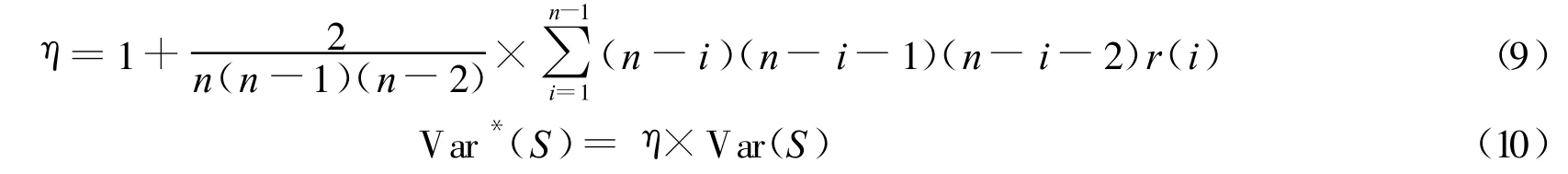
式中，Var(S)为利用式(4)计算的假设序列独立情况下统计量S的方差估计量.将Var*(S)带入式(5)，求出MMK趋势检验方法的统计量，可进一步依据所设定的显著性水平判定序列趋势的显著性.

1.3 序列趋势演变

趋势具有时段性，同一序列不同时段趋势性往往存在很大差别.为了能更好地把握序列趋势性，弄清时间序列趋势状态演变过程十分必要.为此，本文分别通过分析时段的延伸和回溯来研究序列趋势的演变过程，记为趋势演变的F过程和B过程，即，forward，向前，backward，回溯.分别运用MK，MMK趋势检验方法对2种模式下各时段的趋势性进行检验，用时段趋势统计量的变化过程来描述序列趋势演变过程.由于MK(MMK)趋势检验方法的统计量Uc(U*c)在序列长度大于10时近似服从标准化正态分布[11]，故本文F，B过程的分析时段最短均为11a.对于F过程，各时段均以序列起始年份为起始点，第1个时段为从起始年开始的11年，之后以1年为步长，分析时段逐年增加直到序列末端年份.对于B过程，各序列均以序列末端年份为末点，第1个时段为以末端年份为末年向前推至第11年的时段，之后以-1年为步长逐渐向序列起始年份靠拢，直到序列起始年份.

1.4 累积离差过程

对于时间序列X={x1，x2，…，xn}，累积离差定义为:

2 结果分析

2.1 数据资料

本文基于香港地区天文台(Hong Kong Observatory)提供的1947年4月1日—2007年3月31日香港地区逐日降水量序列，通过累加得到研究区雨季(4—9月)、干季(10月—次年3月)、水文年(4月—次年3月)降水量序列.1个水文年包含雨季与干季两季.如，从1955年4月到1956年3月即为水文年的1955年.图1为香港地区1947—2006(水文)年雨季、干季、水文年降水序列，雨季和干季降水量差别明显，超过80%的年降水量集中于雨季.

2.2 序列整体趋势分析

图2为研究区雨季、干季、水文年降水趋势序列{yi}ni=1的前20阶秩次自相关系数的估计值r(k).各序列相关函数值主要在[-0.15，0.15]之间取值，均属于弱相关序列.因此，本文只考虑序列1阶自相关系数的影响，用r(1)，MMK趋势检验方法进行检验.

图1 香港地区雨季、干季、水文年降水序列Fig.1 Precipitation series during wet season，dry season and water year in Hong Kong

图2 降水趋势序列{yi}ni=1的秩次自相关函数Fig.2 Rank-based autocorrelation function of precipitation trend series{yi}ni=1in rank

表1为各序列根据MK，MMK趋势检验方法分析的结果.Uc0，Uc1分别为假设序列独立和考虑序列1阶自相关系数影响的序列趋势统计量;p0，p1为相应的p值:

式中:Φ(.)为标准化正态分布函数.

p0，p1描述了序列对于无趋势原假设的支持率.由表1可见，各序列均呈上升趋势，其中干季降水序列趋势最弱，雨季次之，水文年较雨季略大.比较MK与MMK趋势检验方法的计算结果可知，由于雨季、干季序列的r(1)＜0，导致忽略相关性时对趋势显著性水平的低估;而水文年序列由于r(1)＞0，导致假设序列独立情况下对趋势显著性水平的高估.同时可知，序列趋势统计量对相关性十分敏感，水文年序列r(1)=0.02，考虑此相关性的影响即导致统计量由1.091变为1.067.对于相关性强的序列，在进行趋势检验分析时忽略序列相关性将导致明显的趋势判断误差.总体而言，研究区1947—2006年雨季、干季、水文年各序列均表现为上升趋势，但在0.05显著性水平下趋势性均不是统计显著的.

表1 各降水序列趋势检验结果Table 1 Results of trend tests on various precipitation series

2.3 趋势演变过程分析

图3(a)为趋势演变的F过程，描述了随着时间的延伸降水趋势的变化过程.坐标起始点为1947—1957年这11年的降水趋势统计量;末点为1947—2006年整个序列的降水趋势统计量.图3(b)为趋势演变的B过程，描述了随着分析时段起始年的不同，降水趋势的变化过程.坐标起始点为1947—2006年间的降水趋势统计量;末点为1996—2006年这11年的降水趋势统计量.由于F过程起点固定，故用时段末点年指代整个时段，如，F过程的1947—1957年这个时段，用1957年指代;对于B过程则用各时段起始点年份指代.各时段MK，MMK趋势检验方法检验的结果分别用Uc0，Uc1表示;特别说明的除外，用Uc统一指代Uc0，Uc1，并以显著性水平0.05判定时段趋势性显著与否.

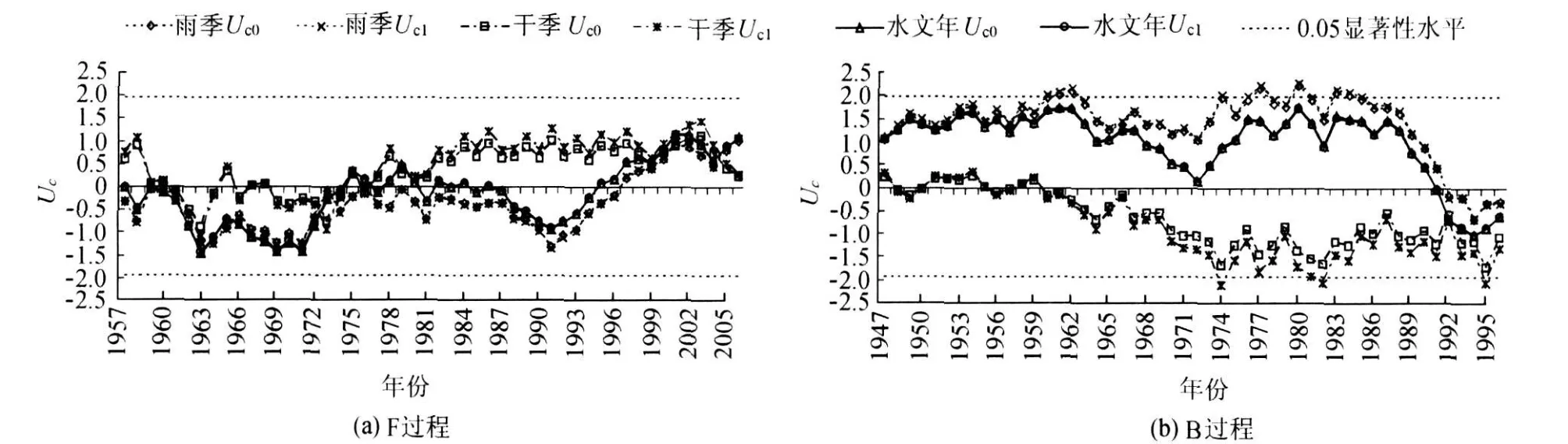
图3 香港地区降水序列趋势演变Fig.3 Trend evolution of precipitation in Hong Kong

从图3(a)可知:研究区雨季、干季、水文年降水从1947年开始，随着时间的延伸，时段趋势状态和显著性水平均处于持续变化中.雨季、水文年均持续较长时间的下降趋势，之后逐步呈现上升趋势;干季早期时段在经过了数次趋势状态的振荡变化后，较雨季、水文年早地表现出上升趋势.整体上，各序列前期均持续了不同时间的下降趋势，之后逐步呈现上升趋势，且各时段趋势性在0.05显著性水平下均不是统计显著的.同时，由序列趋势的F过程可知:降水趋势是非线性变化的;趋势状态和强度均具有一定的持续性，会持续数个时段表现出相同的趋势状态或相近的显著性水平.

从图3(b)可知:从1947年开始，随着分析时段起点年逐步向前推进，雨季、水文年的时段趋势状态均由上升转为下降;干季在维持了数个时段的无趋势状态之后，持续表现出下降趋势.雨季、水文年近期降水(1992—2006年)表现出下降趋势，而参照早期降水情况则持续表现为上升趋势.干季近期较长时间内持续表现为下降趋势，且部分时段的趋势显著性水平超过0.05;当考虑早期(1947—1960年)降水情况时，各时段的趋势性则不再明显.可见，时段起点对于时段趋势状态及显著性均有很大的影响.

由各序列的F和B过程可知:总体趋势性不显著的雨季、干季序列，均包含多个显著性水平超过0.05的时段;总体呈一定上升趋势的各序列均有相当一部分时段表现出下降趋势.对比各序列F，B过程的Uc0，Uc1可知，趋势显著性水平对于相关性十分敏感，尤其是对于趋势性相对明显的时段.因此，对于相关性相对明显的序列，忽略序列相关性将会给趋势显著性水平造成严重的估计误差.无论是F过程还是B过程，雨季与干季的趋势状态、演变过程均存在明显差异，二者有一定的补偿效果，这使得水文年降水序列维持相对平稳的状态，反映了降水年内分配变化与年际平稳的状态.

2.4 趋势的形成与持续

趋势统计量Uc是无参数统计量，只依赖于时段内变量的秩次，不受序列任何统计参数的影响.降水序列的累积离差过程为降水量在序列均值水平上下浮动的累积变化过程，各时刻的离差均要受到序列均值的影响.序列趋势演变过程任意时刻的效果均不会受到“将来”的影响，完全是各时段自我属性的反映;而序列累积离差则反映了序列的整体属性，及在整体属性约束下局部展现出的特性.以下通过降水序列趋势演变过程与其累积离差过程的对比，分析序列局部趋势演变与整体属性的关系.

图4 香港地区雨季、干季、水文年降水序列的累积离差过程Fig.4 Cumulative deviation processes of precipitation series during wet season，dry season and water year in Hong Kong

时段趋势统计量Uc＜0，说明该时段内后期降水量较前期降水量平均偏少;Uc的持续减小，表明时段降水“前丰后枯”格局的加强.若时段趋势统计量Uc＞0，情况则相反.同时，Uc的陡增猛降，表明降水量较时段前期平均水平差别显著;Uc的相对稳定说明降水量相对于时段平均水平的平稳波动.图4为雨季、干季、水文年各降水序列的累积离差过程.

将序列累积离差与其时段趋势统计量的F过程(图3(a))进行比较，发现:雨季序列各时段的累积离差与其时段趋势统计量在任意时段均是同增共减波动方向一致;干季序列除了在1958，1960，1967，1968，1971，1981，1988，2003年累积离差较前一年减小，而对应时段的趋势统计量却均较前一时段增大外，其余时段均是同增共减一致波动;水文年序列除了在1970，1984年累积离差较前一年减小，而对应时段的趋势统计量却均较前一时段增大外，其余时段均是同增共减.由于干季在1974，1978，1982年的降水异常(图1)，使得序列中降水量大于该平均水平的年份明显少于降水量处于该均值水平以下的年份;另外由于干季序列相关性较大，容易出现降水量持续数年处于相近的水平.这两方面的原因导致部分时段降水量的中值明显小于序列平均值，从而出现累积离差较前一时段减小，而相应的趋势统计量却较前一年增大的情况.因此，各序列时段趋势统计量和其累积离差与其前一时段的量值基本为同增共减波动一致，表明各时段降水的平均水平均与序列整体平均水平接近，序列具有较好的平稳性.

趋势状态所描述的是现状水平较前期水平的平均变化倾向，分析时段的前期水平是趋势状态的基石.将序列累积离差与其时段趋势统计量的B过程(图3(b))进行比较，可知序列的枯丰结构对于趋势状态及显著性水平影响很大.丰水期到枯水期的转变过程往往表现出明显的下降趋势;反之，表现为上升趋势.而时段中完整的枯丰转化对于趋势状态及显著性水平影响不大.如，水文年B过程中的时段1972与1990，具有相同的趋势状态，且显著性水平十分相近，时段1972—1990的趋势变化过程以1982年为中心表现出很好的对称性.这一过程特性均与累积离差过程中1972—1990的对称变化(完整的丰枯转换)是一致的.可见，如果分析时段的起点年处于降水相对稳定的阶段，则时段起点年的前后变动对于趋势状态影响不大;但若起点年处于丰水期或枯水期中，则起点年的选取会对分析结果产生比较大的影响.因此，在进行趋势分析时，将累积离差过程和趋势演变过程相结合才能很好地理解趋势特性及其形成原因.同时，基于累积离差过程可以针对不同的研究目的，选择相应的分析时段进行趋势分析.

3 结 语

本文基于香港地区1947—2006年雨季、干季、水文年降水序列，对该地区的降水趋势性进行分析.结果表明:研究区在1947—2006年雨季、干季、水文年降水序列均表现出一定的上升趋势，但各序列趋势在0.05显著性水平下均不是统计显著的，其中，雨季及水文年降水趋势性相对明显.雨季、水文年序列相关性很弱，对序列趋势显著性影响不大;而干季序列的相关性相对较强(r(1)=-0.21)，对序列趋势显著性有较明显的影响.各序列前期均维持了不同时间的下降趋势，后逐步由下降转为上升趋势.雨季与干季的趋势状态、演变过程存在明显差异，二者有一定的补偿效果;水文年降水序列的趋势变化平稳，反映了降水年内分配变化与年际平稳的状态.基于各降水序列趋势演变过程，及其与累积离差过程的对比分析可知，研究区降水趋势性不显著，各序列各时段的趋势状态及其转换过程均属于降水过程中正常枯丰转换的阶段体现.

对于水资源管理而言，尽管研究区近期处于水源相对丰富的丰水期，但丰水期降水量显现出弱的下降趋势.在丰水期延续的同时，枯水期可能也在逼近.因此，需要密切关注降水趋势的变动，做好水资源的相关规划.F过程从正向反映了研究区对某一固定起点水平而言不同时段所表现的趋势状态，揭示了序列趋势的形成过程;B过程则分析了现状水平就不同的参照而言其所呈现出的趋势，可以更灵活地分析近期关注时段的趋势状态.建议在进行趋势分析时，应结合序列趋势的F过程与B过程，既通过F过程分析序列趋势的形成过程，又通过B过程分析变量的最新走势.整体平稳的序列包含了趋势显著性水平较高的时段，说明趋势具有尺度属性.在某时段范围内显著的趋势，可能只是更大尺度范围内的正常波动，这一特征对于依据趋势显著性水平进行序列平稳性判断有重要启示，在以后的研究中需要重点关注.

[1]MANN H B.Non-parametric test against trend[J].Econometric，1945，13:245-259.

[2]徐利岗，周宏飞，李彦，等.中国北方荒漠区降水稳定性与趋势分析[J].水科学进展，2008，19(6):792-799.(XU Li-gang，ZHOU Hong-fei，LI Yan，et al.Analysis of the precipitation stability and variety trend in the desert region of northern China[J]. Advances in Water Science，2008，19(6):792-799.(in Chinese))

[3]王志福，钱永甫.中国极端降水事件的频数和强度特征[J].水科学进展，2009，20(1):1-9.(WANG Zhi-fu，QIAN Yong-fu. Frequency and intensity of extreme precipitation events in China[J].Advances in Water Science，2009，20(1):1-9.(in Chinese))

[4]MELEOD A I，HIPEL K W.Preservation of the rescaled adjusted range 1:a reassessment of the hurst phenomenon[J].Water Resources Research，1978，14(3):491-508.

[5]ZETTERQVIST L.Asymptotic distribution of Mann's test for trend m-dependent seasonal observations[J].Scandinavian Journal of Statistics，1988，15(2):81-95.

[6]HAMED K H，RAO A R.A modified Mann-Kendall trend test for autocorrelated data[J].Journal of Hydrology，1998，204(1/4):182-196.

[7]HAMED K H.Trend detection on hydrologic data:the Mann-Kendall trend test under the scaling hypothesis[J].Journal of Hydrology，2008，349(3/4):350-363.

[8]ADAMOWSKI K，BOUGADIS J.Detection of trends in annual extreme rainfall[J].Hydrological Processes，2003，17:3547-3560.

[9]KHALIQ M N，OUARDA T BM J，GACHON P.Identification of temporal trends in annual and seasonal low flows occurring in Canadian rivers:the effect of short-and long-term persistence[J].Journal of Hydrology，2009，369(1/2):183-197.

[10]MANN H B.Nonparametric tests against trend[J].Econometrica，1945，13:245-259.

[11]KENDALL M G.Rank correlation methods[M].London:Griffin，1975.

[12]SEN P K.Estimates of the regression coefficient based on Kendall's tau[J].American Statistic Association，1968，63:1379-1389.

[13]丁晶，邓育人.随机水文学[M].成都:成都科技大学出版社，1988:34-37.