水文时间序列的相似性搜索研究

欧阳如琳,任立良,周成虎

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室,北京 100101)

自20世纪90年代以来,随着数据库技术的成熟和数据应用的普及,人类积累的数据量正在以指数速度迅速增长.面对浩瀚无垠的数据,人们迫切需要新的技术和自动化工具将海量数据转化为有用的信息和知识.数据挖掘(data mining,DM)技术在这样的背景下应运而生,并越来越显示出其强大的生命力.所谓数据挖掘,就是从大量的、不完全的、有噪声的、模糊的、随机的实际应用数据中,提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程[1].以时间序列为挖掘对象的数据挖掘,称之为时间序列数据挖掘(time series data mining,TSDM).由于时间序列数据的广泛存在性,使得时间序列数据挖掘成为学术界的研究热点之一,取得了显著的研究成果[2-12],其中,时间序列相似性搜索是时间序列数据挖掘中研究最为广泛也是发展最为成熟的.

水文过程受确定性因素和不确定性因素的共同作用,确定性因素的作用使得水文过程表现出年、季节甚至日等周期性变化.如日、旬、月流量过程明显存在以年为周期的变化.这是由于影响水文过程的主要因素——气候因素存在以年为周期的季节性变化,这种水文过程中年际间的周期性可视为水文过程年际间的相似性.同样,由于受一次降水量的过程影响,一场洪水过程都是由起涨到达顶峰最后消退的过程,年内汛期洪水总趋势与场次洪水过程间具有相似性.这是由于西风带、季风活动、副热带高压等天气系统的季节性活动的相似性,形成的暴雨以及相应的洪峰流量及其洪水过程在年内季节间具有相似性[13-14].水文过程的形成和演变还受到许多随机因素的影响,比如流域内的地形、地势、土壤、植被以及降水的时空分布等,使得水文过程年际间的相似性和场次洪水的相似性只能是某种程度上的相似,而并非完全相同.传统水文过程的相似性研究强调精确匹配,实际的水文过程本身很难达到如此要求,而数据挖掘中,一般采用基于近似匹配的“近似”相似性搜索[15],符合水文数据的特点.本文将数据挖掘中的相似性搜索方法和技术引入水文时间序列分析研究中,探索适合水文数据特点的相似性研究方法,挖掘相似的水文(流量)过程,发现隐藏在水文数据中有用的信息和知识.

1 相似性搜索

1.1 原理

所谓相似性搜索,就是找出与给定查询序列的变化行为最为接近的数据序列.给定一个目标模式X=(x1,x2,…,xn)和一个序列Y=(y1,y2,…,ym),相似性问题就是如何确定X和Y的相似度sim(X,Y).这里n和m的取值可以相同也可以不同,当n=m时就是这两个序列完全匹配(whole sequence matching)的问题,即从具有相同长度的序列中查找相似的序列;如果n≠m就是子序列匹配(subsequence matching)问题,即从yi(i=1,2,…,m-n+1)开始,找出Y中与X最相似的子序列(假定n＜m).

无论哪一种相似性的搜索都依赖于时间序列的相似性度量方法,即如何定义sim(X,Y).目前时间序列相似性的度量主要是基于距离的度量.给定一个计算序列间的距离公式,并确定一个距离阈值,对任意给定的两序列,当距离小于或等于阈值时,则认为两序列相似,否则,认为二者不相似.因为长度为n的时间序列可以看做是n维空间上的点,所以空间距离函数可以用作序列距离公式.而最困难的是,如何定义序列间的距离.在时间序列相似性搜索中最常用的是欧几里得距离(Eculidean distance),也称欧氏距离.

假定两个时间序列X=(x1,x2,…,xn)和Y=(y1,y2,…,ym),当n=m时,它们的欧氏距离定义为

欧氏距离虽然比较简单,但是在相似性的度量中却很不可靠,这是因为时间轴的微小变形将会引起欧氏距离很大的变化,因此对时间轴有轻微变形的时间序列相似性的测量,欧氏距离将不再适用,如图1所示.虽然两个时间序列的形状相似,但是它们在时间轴上并不是完全对齐的,因此图1(a)中用欧氏距离计算相似性结果的距离将会很大,可能会导致产生不相似的结果.若测量时,时间轴可以根据具体情况进行移动,在两个序列之间寻找一条对齐路径,使得两个序列之间的欧氏距离最小,从而更直观(更类似于人类思考方式)地测量时间序列的相似性,会更有效的找到两个时间序列的相似形状.对于这种情况人们提出了一种新的相似性测量方法——动态时间扭曲(dynamic time warping,DTW)法[16],该方法允许在时间轴上有弹性地移动,以便能够在两个时间序列的不同时间阶段发现相似的波形.动态时间扭曲距离可以适时地转换、扩张或压缩两个序列的局部特征,实现两个序列的同步化,因此动态时间扭曲距离不要求比较序列长度的一致性.最早动态时间扭曲法是用于语音处理领域将时间轴上的模式进行对齐,后来Berndt等[17]将其引入到时间序列数据挖掘中.

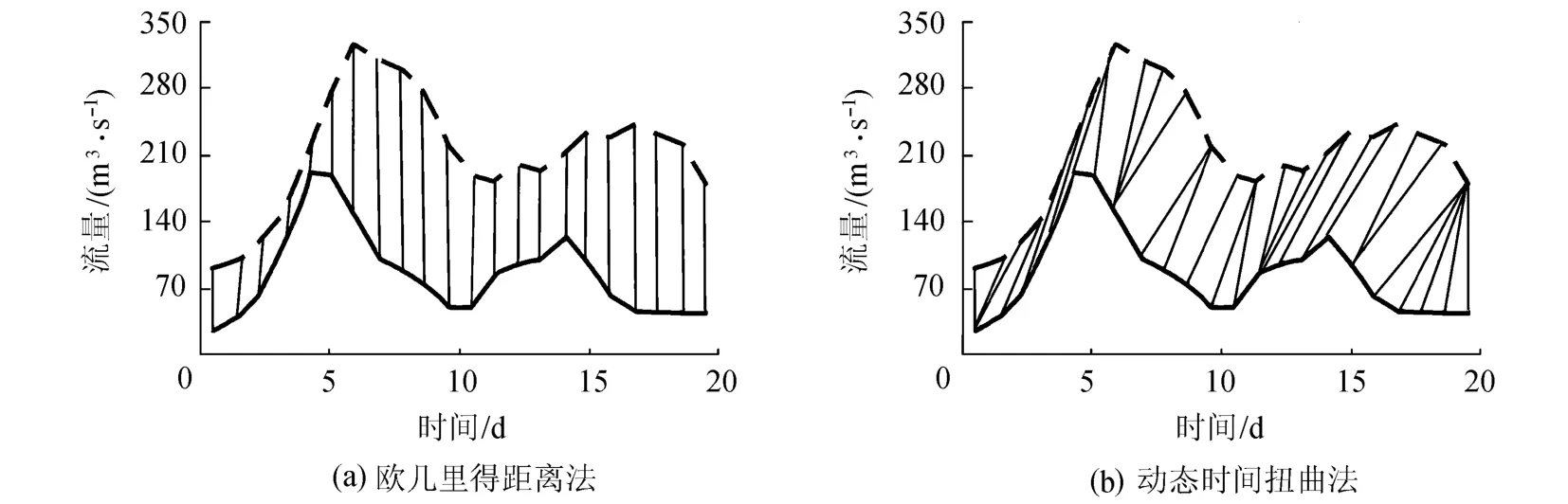
图1 不同的距离度量方法Fig.1 Different distance measuring methods

1.2 动态时间扭曲算法

动态时间扭曲法的计算过程是一个动态最优的计算过程,具体如下[18]:设两个时间序列分别为X=(x1,x2,…,xn)和Y=(y1,y2,…,ym),构建一个m×n阶的矩阵,其中第(i,j)个元素就是两个时间序列的点xi和点yj之间的距离d(xi,yj),通常采用d(xi,yj)=(xi-yj)2计算.如图2所示,一个扭曲路径W就是由上述矩阵元素构成的连续路径,这个路径定义了时间序列X和Y之间的一个映射,W的第k个元素被定义为wk=(i,j)k,因此可以得到一个路径集为

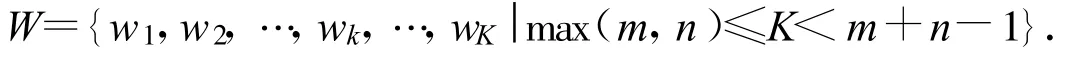
扭曲路径要求满足以下条件限制:

a.边界条件:w1=(1,1),wK=(m,n),即要求扭曲路径必须从矩阵的起始位置处开始和结束位置处结束.

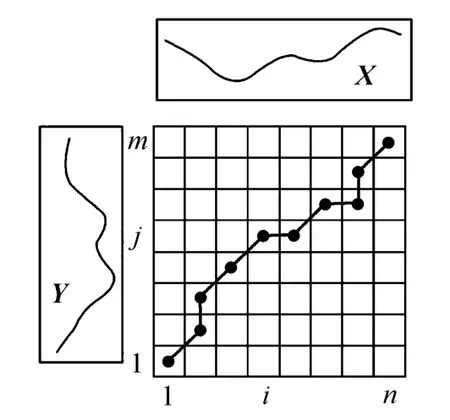
图2 扭曲路径示意图Fig.2 Example of warping path

b.连续性:给定wk=(a,b),wk-1=(a′,b′),要求a-a′≤1和b-b′≤1,即要求扭曲路径每一步的设定都是连续的.

c.单调性:给定wk=(a,b),wk-1=(a′,b′),要求a-a′≥0和b-b′≥0,即要求路径必须在时间轴上是单调的.也就是说,路径W通过点(i,j)同时必须至少通过点(i-1,j-1),(i-1,j)或(i,j-1)中的一个.

很显然满足上述条件的路径有很多,假设可计算每条路径达到点(m,n)时总的累积距离,具有最小累积距离者为最佳路径,即路径满足一个最小的扭曲代价:

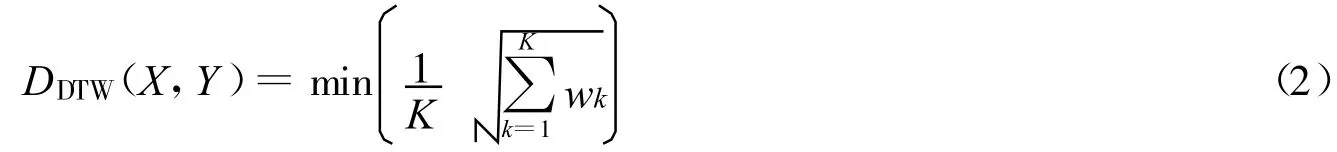
式中,分母K用来消除不同扭曲路径长度的影响.

基于动态最优原理可知,设有点(i,j)在最佳路径上,那么从点(1,1)到点(i,j)的子路径也是局部最优解,也就是说从点(1,1)到点(m,n)的最佳路径可以由时间起始点(1,1)到终点(m,n)之间的局部最优解通过递归搜索获得.构造累积距离矩阵r,点(i,j)计算公式如下:

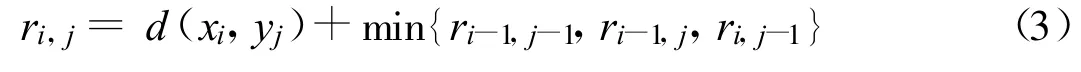
其初始条件为r1,1=d(x1,y1).从两个序列起始点(1,1)开始迭代计算点(i,j)的累积距离,最终时间序列弯曲路径最小累加值为rm,n,即为时间序列X和Y的动态时间扭曲距离.图3显示了两个时间序列X=(3,4,5,6,3,3)和Y=(1,3,2,1)的累积距离矩阵计算过程,最终得到序列X和Y的动态时间扭曲距离为11,灰色格子为最佳路径.

图3 时间序列 X=(3,4,5,6,3,3)和Y=(1,3,2,1)的累积距离矩阵计算过程Fig.3 Cumulative distance matrix for computing dynamic time warping distance between X=(3,4,5,6,3,3)and Y=(1,3,2,1)

2 水文时间序列的相似性搜索

2.1 计算步骤

在水文过程中,季节性的水文过程往往表现出一定的相似性,这是由于影响水文过程的气候因素,在每年的同一个季节中变化较一致,但也不是完全一致.例如,在夏季,经常出现由暴雨而产生的洪水过程,这样的过程往往是具有相似性的,但具体出现的日期往往不是每年的同一天,有可能会错开几天,在这样的情形下,如果采用欧式距离来度量两个洪水过程,得到的结论往往是两个过程不相似,而如果采用动态时间扭曲算法,就有可能发现在不同时间出现的相似过程.

本文选取塔里木河流域源流区出山口水文站沙里桂兰克站1961—2000年共220场洪水作为相似性搜索的挖掘对象,采用动态时间扭曲距离度量,挖掘相似的水文时间序列过程.计算步骤如下:

a.对220场洪水,分别进行标准化.假设某场洪水过程的流量时间序列为(q1,q2,…,qn),采用零-均值标准化方法对其进行标准化,计算公式如下:

b.对标准化后的220场洪水过程,两两进行动态时间扭曲距离的计算.

c.用一个220行220列的矩阵来存放计算得到的各场次洪水之间的动态时间扭曲距离,称之为相似性距离度量矩阵:

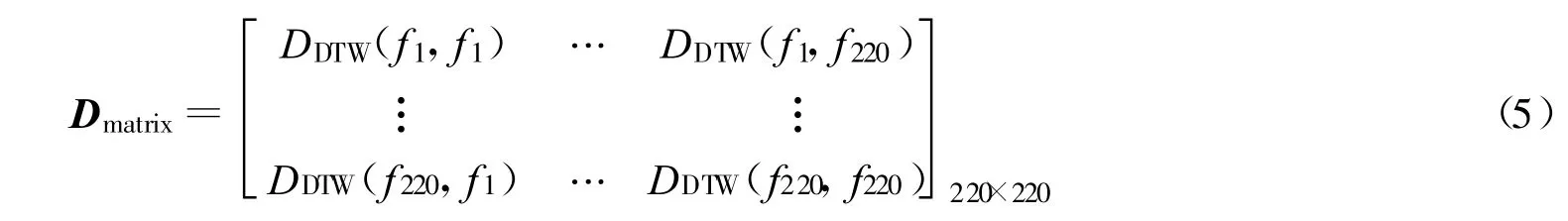
式中f1,f2,…,f220为这220场洪水的代号.Dmatrix是一个对称矩阵,矩阵的第(u,v)元素代表第u场洪水和第v场洪水之间的动态时间扭曲距离,即DDTW(fu,fv).矩阵对角线为0,表示同一场洪水自身的动态时间扭曲距离为0.矩阵内元素的值越小,相应的两场洪水的动态时间扭曲距离越小,则这两场洪水过程越相似;反之,元素值越大,即相应的两场洪水的动态时间扭曲距离越大,则两场洪水过程越不相似.

d.除去对角线的0元素,从矩阵中选取元素值较小时所对应的洪水,即为挖掘得到的相似的洪水过程.

2.2 计算结果

塔里木河流域源流区地域广阔,气候和地形变化复杂,从而形成了类型多样、特征各异的洪水,按其洪水成因,可分为暴雨型洪水、融雪型洪水、混合型洪水和冰川湖溃决洪水[19].不同类型的洪水表现出不同的洪水流量过程形态,同种类型且相同条件下形成的洪水表现出相似的洪水流量过程形态.图4为部分从相似性距离度量矩阵中挖掘得到的相似洪水过程.从图4中可以发现,本研究流域的洪水过程形态多样,有中等流量陡涨缓落型洪水(图4(a))、大流量的陡涨陡落型洪水(图4(b))、矮胖型洪水(图4(c)和图4(d))、双峰型洪水(图4(e))和无明显洪峰的洪水(图4(f)).从相似性搜索中挖掘出相似的洪水过程,说明这些洪水过程具有一定出现的频率,也往往隐藏着相似的洪水成因.

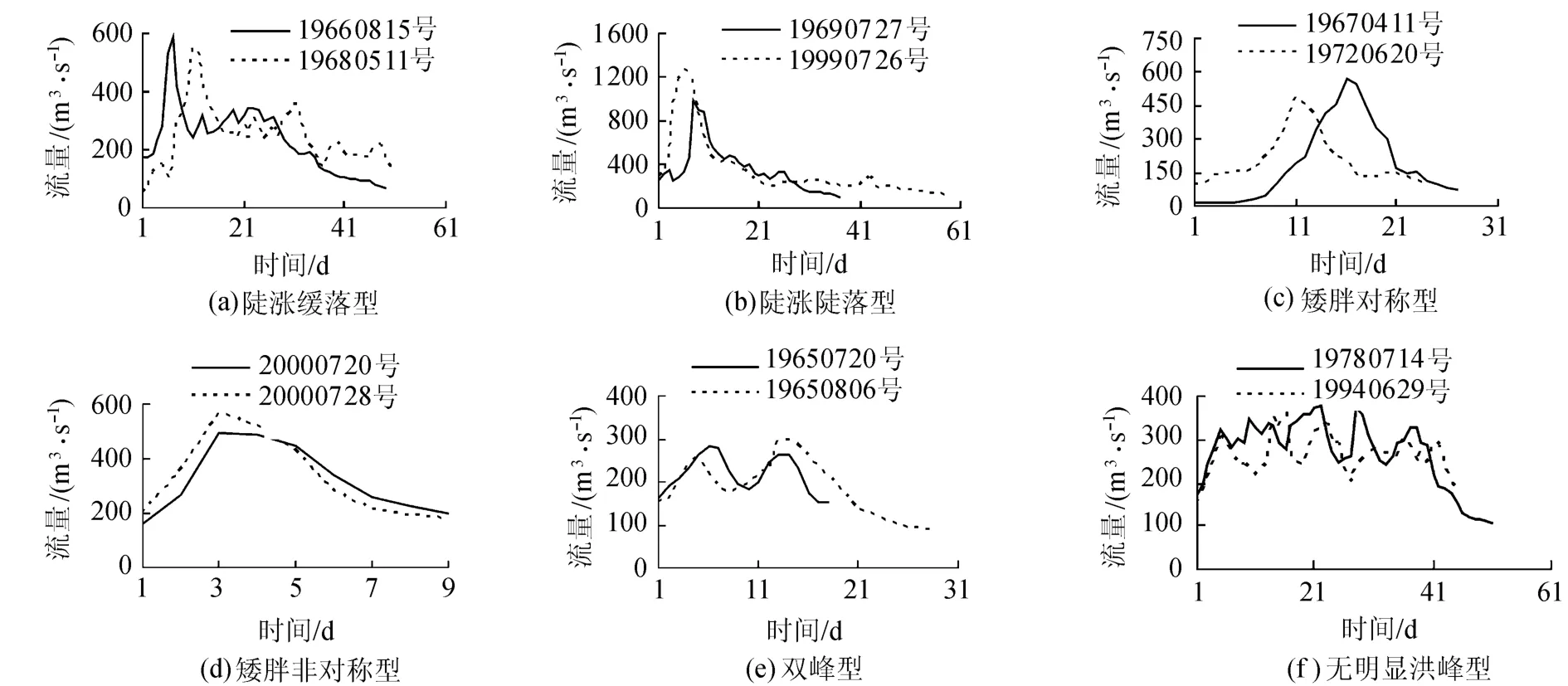
图4 相似的洪水流量过程线Fig.4 Similar flood discharge hydrographs

3 结 语

本文将时间序列相似性搜索的数据挖掘方法应用于水文过程的相似性研究中,在分析欧氏距离和动态时间扭曲距离两种相似性距离度量方法特点的基础上,采用对时间轴的伸缩和弯曲具有较好适应性的动态时间扭曲距离法对洪水流量过程进行相似性距离度量,搜索挖掘出相似的洪水流量过程.实例结果表明,动态时间扭曲距离法适合水文数据的特点,能有效挖掘出相似的水文过程.今后值得研究的问题是,水文时间序列相似性搜索如何进一步与数据挖掘中聚类和分类的算法相结合,进一步对场次洪水过程进行相似性类型的划分,从相似的洪水类型中分析其相似的物理成因和机制,从而发现隐藏在相似过程中的确定性规律.

[1]FAYYAD U M,PIATETSKY-SHAPIRO G,SMYTH P,et al.Advances in knowledge discovery and data mining[M].Menlo Park,California,USA:AAAI Press,1996:307-328.

[2]ROSENSTEIN M T,COHEN P R.Conceptsfrom time series[C]//The American Association for Artificial Intelligence.Proceedingsof the Fifteenth National Conference on Artificial Intelligence(AAAI-98).Menlo Park,California,USA:AAAI Press,1998:739-745.

[3]MAMNILA H,TOIVONEN H,VERKAMO A I.Discovering frequent episodes in sequences[C]//FAYYAD U M,UTHURUSAMY R.Proceeding of the First International Conference onKnowledge Discovery and Data Mining(KDD-95).Menlo Park,California,USA:AAAI Press,1995:210-215.

[4]AGRAWAL R,IMIELINSKI T,SWAMI A N.Mining association rules sets of items in large databases[C]//BUNEMAN P,JAJODIA S.Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data.New York:ACM Press,1993:207-216.

[5]DAS G,LIN K I,MAMNILA H,et al.Rule discovery from time series[C]//AGRAWAL R,STOLOR Z P E,PIATETSKY-SHAPIRO G.Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining(KDD-98).Menlo Park,California,USA:AAAI Press,1998:16-22.

[6]HAN J W,YIN Y W,DONG G Z.Efficient mining of partial periodic patterns in time series database[C]//KITSUREGAWA M,MACIASZEK L,PAPAZOGLOU M,et al.Proceeding of the Fifteenth International Conference Data Engineering(ICDE 1999).Los Alamitos,California,USA:IEEE Computer Society Press,1999:106-115.

[7]BETTINI C,JAJODIA S,WANG S.Time granularities in databases,data mining and temporal reasoning[M].New York:Springer-Verlag,2000.

[8]POVINELLI R J.Time series data mining:identifying temporal patterns for characterization and prediction of time series events[D].Milwaukee,Wisconsin:Marquette University,1999.

[9]HAN J W,KAMBER M.Data mining:concepts and techniques[M].San Francisco,USA:Morgan Kaufmann,2001.

[10]曾海泉.时间序列挖掘与相似性查找技术研究[D].上海:复旦大学,2003.

[11]张保稳,何华灿.时态数据挖掘研究进展[J].计算机科学,2002,29(2):124-126.(ZHANG Bao-wen,HE Hua-can.Progress of temporal data mining research[J].Computer Science,2002,29(2):124-126.(in Chinese))

[12]荣冈.时间序列数据挖掘研究与应用[D].杭州:浙江大学,2004.

[13]侯玉,吴伯贤,郑国权.分形理论用于洪水分期的初步探讨[J].水科学进展,1999,10(2):140-143.(HOU Yu,WU Bo-xian,ZHENG Guo-quan.Preliminary study on the seasonal periods classification of floods by using fractal theory[J].Advances in Water Science,1999,10(2):140-143.(in Chinese))

[14]方崇惠,雒文生.分形理论在洪水分期研究中的应用[J].水利水电科技进展,2005,25(6):9-13.(FANG Chong-hui,LUO Wensheng.Application of fractal theory to stage research of flood events[J].Advances in Science and Technology of Water Resources,2005,25(6):9-13.(in Chinese))

[15]吴德.水文时间序列相似模式挖掘的研究与应用[D].南京:河海大学,2007.

[16]SAKOE H,CHIBA S.Dynamic programming algorithm optimization for spoken word recognition[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1978,26(1):43-49.

[17]BERNDT D,CLIFFORD J.Using dynamic time warping to find patterns in time series[C]//FAYYAD U M,UTHURUSAMY R.AAAI-94 Workshop on Knowledge Discovery in Databases(KDD-94).Menlo Park,California,USA:AAAI Press,1994:229-248.

[18]KEOGH E,PAZZANI M.Derivative dynamic time warping[C]//KUMAR V,GR OSSMAN R.Proceedings of the First SIAM International Conference on Data Mining(SDM'2001).Philadelphia,PA,USA:SIAM,2001:1-11.

[19]新疆维吾尔自治区水利厅,新疆水利学会.新疆河流水文水资源[M].乌鲁木齐:新疆科技卫生出版社,1998:144.