动脉血管 STL模型边界识别及其三角剖分

付文宇,乔爱科,付鹏斌

(1.北京工业大学机械工程与应用电子技术学院,北京 100124;2.北京工业大学生命科学与生物工程学院,北京 100124;3.北京工业大学计算机学院,北京 100124)

在对人体动脉血管进行流体力学分析时,为了得到准确的结果,一般需要进行计算流体动力学分析(computational fluid dynamics,CFD).血液流动仿真可以给医生提供许多人体数据信息,帮助他们进行手术规划[1].要进行计算流体动力学分析,需对模型进行网格划分.和真实血管几何形状较为接近的动脉血管模型的构建方法为:根据计算机断层扫描技术(CT)或核磁共振成像(MRI)等技术获得血管二维断层图像,然后采用表面绘制(surface rendering)或者体绘制(volume rendering)技术获得相应模型.通过表面绘制方法,可以获得以 STL文件表示的动脉血管表面模型.有时 STL文件表示的表面模型并不是封闭的,而进行体网格划分的前提是其表面模型必须封闭.因此,必须找到合适的方法将开口边界区域封闭起来.一些网格划分软件有一定的 STL文件编辑功能.比如 NETGEN[2]具有一个 STLDoctor工具,利用它可以对 STL文件表示的模型进行一定的编辑操作,如通过鼠标双击模型上某一个三角面片,就可以获得三角面片顶点坐标,这样通过逐个选择处于边界的三角面片就可以获得相应边界点坐标,但这种方法复杂且易出错.若能将 STL文件表示的表面模型的点、线、三角面片之间的关系表示出来并利用处于开口边界的边只属于一个三角面片这一特性,就可以将开口边界识别出来.张翔等[3]对 STL文件的拓扑重建方法进行了研究;候宝明等[4]对 STL文件拓扑重建及其缺陷修复进行了研究.但他们的研究是从逆向工程的角度出发,面向快速成型制造,并不关心开口边界识别及其三角剖分问题.本文对具有开口边界的 STL文件的拓扑重建、边界识别以及使用 Delaunay三角剖分封闭识别的边界问题进行研究,并编程实现此功能.

1 拓扑结构重建

要对 STL文件进行拓扑重建,需知道 STL文件数据结构,其详细信息参见文献[5-7].由于 STL文件只给出实体表面三角面片的点坐标及其法线向量,因此任何一个可以完整表示多面体的数据结构均可以表示 STL文件的拓扑关系.例如,半边结构(half-edge structure)[8]、翼边结构(wing-edge structure)[9]等.如果使用半边结构重建 STL模型的拓扑结构并应用一个只有半边没有伙伴半边的边查找过程,就能将STL模型开口边界识别出来,因此,本文选择半边结构作为拓扑重建的数据结构.

本文中使用的半边结构同文献[8]中的略有不同,由于在每个 STL文件表示的三角面片中均没有内部孔,为了使数据结构更为紧凑,不用圈(loop)节点,而只使用以下 5个节点:体(solid)、面(face)、边(edge)、半边(half-edge)、顶点(vertex).体节点形成了 1个半边结构实例的根节点.体节点中包含指向面、边、顶点的双向链表的指针,通过它可以访问相应的面、边、顶点.面节点表示多面体中的 1个平面,其中包含指向面所属体的指针以及面链表中前、后面的指针.半边表示 1条有向线段,3条首尾相接的半边构成 1个三角面片,2个相邻的三角面片一定存在 1对重合的、方向相反的半边,称为伙伴半边.2个伙伴半边一起构成 1条整边(父边),如图 1所示.每个半边结构中都包括 1个指向它所属父边的指针、1个指向半边开始顶点的指针以及指向相连接的前、后半边的指针.边节点包含属于它的左右 2个半边的指针以及边链表中前、后边的指针.顶点节点包含 1个指向它所属半边的指针、顶点的坐标值以及顶点链表中前、后顶点的指针.

拓扑结构重建过程是在一个 while(C++)循环过程中完成的,在 while的一次循环过程中,读入 STL文件的 1个三角面片数据,即三角面片 3个顶点坐标.先检查三角面片的 3个顶点在已建立的模型中是否存在,如果存在,就不建立新的顶点节点;否则,建立新的顶点节点.顶点的查找过程借助一个动态平衡二叉树(AVL TREE)来实现,这样做的原因是表征血管的 STL文件包含的数据量非常大,一个较小文件也会包含几万个顶点,具体实现方法见文献[10].顶点节点处理完后,建立该三角面片的 1个新的面节点和3个新的半边节点,并且建立这 3个半边和顶点、三角面片的对应关系.由于 STL文件中每个三角面片都会对应 1个且是唯一 1个面节点及 3个半边节点,因此在已建立的模型中肯定不会出现表示现在这个三角面片及其 3个半边的节点,只需生成新的节点即可.然后建立新生成的 3个半边和父边的关系,这里要分 3种情况分别进行处理:

1)如果某半边的起点或终点是新建顶点,则该半边所属的边是不存在的,这时直接在已建立的模型中建立 1个新的边节点,同时将该半边设置为新边的 1个半边;

2)通过对动态 AVL树进行查找,某半边的起点和终点在已建立模型中都存在,则进一步查找这 2个点是否曾组成 1个半边,如果有,则说明这个半边的伙伴半边一定存在,此半边的父边节点在模型中已经存在.这时将查找到的半边设置为伙伴半边,同时设置此半边(新生成的半边)与父边的关系;

3)通过对动态 AVL树进行查找,某半边的起点和终点在已建立模型中都存在,则进一步查找这 2个点是否曾组成 1个半边,如果没有,则说明这 2个点分属于不同的 2个三角面片,需新生成 1个边节点,同时将该半边设置为新边的 1个半边.

通过以上过程,将生成 4个双向链表,即体链表、面链表、边链表、顶点链表,还有表示三角面片 3个互相连接半边的半边链表(双向循环链表).需要指出的是拓扑重建完成后,体链表、面链表、边链表、顶点链表各只有 1个.而 1个三角面片就对应 1个半边链表,有多少三角面片就生成多少半边链表.

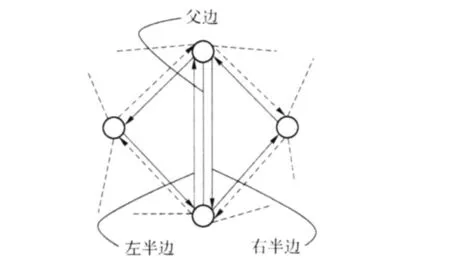
图 1 半边与边关系Fig.1 Relation between halfedge and edge

2 实体边界识别

能将实体边界识别出来是基于这样一个简单的事实:处于边界上的三角面片边,在拓扑重建完成后,在拓扑结构中将只有 1个半边以及边,而没有伙伴半边,如图 2所示;而不处于边界上的三角面片边,在拓扑重建完成后,将有 1个半边及其对应的伙伴半边和边,如图 1所示.

边界识别过程分为 2个步骤:

1)将 STL文件表示实体的所有边界点全部提取出来;

2)在步骤 1)的基础上,将各个单独的封闭边界点集从全部边界点集中提取出来.

步骤 1)是通过一个边查找函数实现的,其核心代码如下(用 C++实现):

其中,ptEdge是此边查找函数的传入变量,表示拓扑重建后形成的边链表的首地址;he1和 he2是边节点中的 2个成员变量,分别表示 1个边的左、右半边节点地址.如果 1个边节点只有 1个半边而没有其伙伴半边,则说明它是 1个边界边,将此边的 2个端点坐标保存到 outputFile文件流对象中,然后通过此文件流对象将数据写入到数据文件中.虽然保存的是点坐标,但实质保存的是各个边界线段.也就是说,第 1、2点组成一个边界边,第 3、4点组成另一个边界边,其余类推.此外,模型中互相相连的边界边在实际查找过程中不一定以连续的顺序存入数据文件,这也是为什么还要执行步骤 2)的原因.

步骤 2)是通过 5个子过程实现的:

①将步骤 1)中提取出来的全部边界点集保存起来.因为点集数目是未知的,所以使用动态数组能将数据保存起来,但是 C++中并没有动态数组这种数据类型.标准C++库提供了一个标准容器“vector”,可以使用vector实例化一个基本数据类型的容器对象,然后将点集元素存入 vector对象.同时,vector还提供了追加、查找、删除等方法,方便了对数据的操作,在后面的几个步骤中均用到了这些方法.

②从步骤 1)形成的 vector对象(下面简称为 v)中提取出第 1个封闭边界.将 v中的第 1个元素(点坐标)存入另一个 vector对象 v1,然后在 v中查找同 v的第 2个元素值相同的另一个元素(记为第 j个元素),找到后存入 v1.这样就将此封闭边界的第 1个边找到,同时也找到了和第 1个边相连的下一个边的开始点(第 j个元素).随后循环进行此过程,直到找到的元素值和 v中的第 1个元素值相同,循环结束.

③将 v中和 v1元素值相同的元素删除.

④重复进行②和③,将余下的各个封闭边界找出,直到 v中不再有任何元素.

⑤将获得的各个封闭边界点坐标输出到相应的数据文件.

图 2 边界边示意图Fig.2 Graph of boundary edge

3 封闭边界区域 Delaunay三角剖分

由于 STL文件是由三角面片组成的表面模型,所以必须将获得的各个封闭边界围成的区域进行三角剖分,才能使 STL文件表示的模型成为一个封闭的表面模型.一种比较简单和自然的三角剖分的方式如图 3所示(实线代表原始的封闭边界),从图 3中可以发现,该方法产生的三角形大部分是狭长的,从进行有限元分析的角度出发,这种三角形的质量不好,不适合进行有限元分析.通过分析,发现产生狭长的三角形是因为三角形的最小角较小,要是能使剖分后生成的三角形的最小角角度较大,将是一种较好的三角剖分方式(理想的形状是等边三角形).

事实上,这是计算几何上的一个经典问题,即 Delaunay三角剖分.设 P为任一平面点集.P的任一角度最优的三角剖分,必是 P的一个 Delaunay三角剖分.此外,在 P的所有三角剖分中,Delaunay三角剖分使最小角达到最大[11].美国的 Jonathan Richard Shewchuk在互联网上公布了专门解决 2D点集 Delaunay三角剖分的程序 Triangle[12],利用这个程序可以非常方便地对 2D点集进行 Delaunay三角剖分.值得注意的是,根据不同的输入,Triangle会对 2D点集进行不同的 Delaunay三角剖分.对于本文的问题,是一个带有约束条件的二维 Delaunay三角剖分,同时应允许在封闭边界内部插入一些点(Steiner点),以便进行较高质量的 Delaunay三角剖分.这里所说的约束条件是指,只允许在边界内部插入点而不允许在边界线段上插入点,否则会产生如图 4所示的不符合 STL文件格式的三角剖分(一个三角面片中的顶点不能落在另一个三角面片的边上).

图 3 三角剖分的一种方式Fig.3 One way of triangulation

图 4 不合适的三角剖分方式Fig.4 An unfitway of triangulation

通过使用 Triangle程序,可以很容易地对各个封闭边界进行 Delaunay三角剖分,同时获得剖分后的各个三角形顶点坐标.

通过使用 C++中文件追加数据的方法,按照 STL文件的格式要求,可将获得的三角面片数据写回STL文件中.图 5是没有经过上述处理而具有开口的 1个 STL文件模型,图 6是经过上述封闭处理后的 1个 STL文件模型.开口表面模型封闭化是进一步有限元体网格划分的关键.

图5 动脉血管模型Fig.5 Model of artery blood

图 6 封闭的动脉血管模型Fig.6 Closedmodelof arteries

4 结束语

本文以动脉血管 STL模型为例,探讨了 STL模型的拓扑重建、开口边界识别及其三角剖分的方法.在此基础上,开发了相应的自动处理软件.文中所述方法和所开发软件不仅适用于动脉血管 STL模型,而且对其他领域的 STL模型同样适用.

[1]ZHANG Y,BAZILEVS Y,GOSWAMI S,etal.Patient-specific vascular NURBSmodeling for isogeometric analysis of blood flow[J].Computer Methods in Applied Mechanics and Engineering,2007,196(29-30):2943-2959.

[2]SCHOBERL J.NETGEN-An advancing front 2D/3D-meshgenerator based on abstract ru les[J].Computing and Visualization in Science,1997,1(1):41-52.

[3]张翔,廖文和,程筱胜,等.STL格式文件的拓扑重建方法研究[J].机械科学与技术,2005,24(9):1093-1096.ZHANG Xiang,LIAO Wen-he,CHENG Xiao-sheng,et al.Study on topology reconstruction of STL file[J].Mechanical Science and Technology,2005,24(9):1093-1096.(in Chinese)

[4]候宝明,刘雪娜.STL实体模型的拓扑重建及其缺陷修复[J].计算机工程,2005,31(3):213-217.HOU Bao-m ing,LIU Xue-na.Topological reconstruction of STL solidsmodel and its errors repair[J].Computer Engineering,2005,31(3):213-217.(in Chinese)

[5]RYPL D,BITTNAR Z.Generation of computational surface meshes of STL models[J].Journal of Computational and App lied Mathematics,2006,192(1):148-151.

[6]赵美利,杨晶,毛红奎,等.基于STL文件格式的实体分割及缺陷修复方法研究[J].系统仿真技术,2008,4(1):35-39.ZHAO Mei-li,YANG Jing,MAO Hong-kui,et al.Research on themethod for dividing a entity and defects repair based on STL file format[J].System Simulation Technology,2008,4(1):35-39.(in Chinese)

[7]王成,曾晓雁.激光三维雕刻中实时切片算法研究[J].工程图学学报,2008,29(1):13-18.WANG Cheng,ZENG Xiao-yan.Real-time slicing algorithm for 3D laser carving system[J].Journal of Engineering Graphics,2008,29(1):13-18.(in Chinese)

[8]MANTYLA M.An introduction to solid modeling[M].Rockville,Maryland:Computer Science Press,1988:168-170.

[9]WEILER K.Edge-based data structures for solid modeling in curved-surface environments[J].IEEEComputer Graphics and Applications,1985,5(1):21-40.

[10]刘金义,侯保明.STL格式实体的快速拓扑重建[J].工程图学学报,2003,24(4):34-39.LIU Jin-yi,HOU Bao-ming.Efficient topological reconstruction of solids in STL format[J].Journal of Engineering Graphics,2003,24(4):34-39.(in Chinese)

[11]BERG M D,KREVELD M V,OVERMARSM,et al.Computational geometry algorithms and applications[M].New York:Springer-Verlag Berlin Heidelberg,1997:191.

[12]SHEWCHUK JR.Delaunay refine mentalgorithms for triangularmesh generation[J].Computational Geometry,2002,22(1-3):21-74.