改进层次分析法和逼近理想解排序法结合在重金属污染评价中的应用*
2010-03-11东南大学流行病与卫生统计学系210009李朝赟孙金芳岳立文
东南大学流行病与卫生统计学系(210009) 李朝赟 孙金芳 胡 丹 岳立文 刘 沛
食品中重金属污染物是造成食源性疾病的重要因素,和其他粮食作物相比,水稻更容易受到重金属的污染,因为金属离子更易融于水中而被水稻吸收,积累在水稻籽粒中,对人类健康造成严重威胁〔1〕。鉴于此,本研究通过对我国工业化水平较高同时污染也较严重的泛长三角五省市 (上海、浙江、江苏、安徽、江西)大米中镉、铅、汞、砷等重金属的 P50及 P97.5值进行综合评定,以了解其污染分布情况。本次研究引入的逼近理想解排序法,相对于国内评价重金属污染常用的单因子指数法、尼梅洛综合指数法、污染负荷指数法等方法〔2〕,具有原理简单、计算简便、排序明确等特点;对数据分布类型、样本含量、指标多少无严格限制。利用改进层次分析法确定数据的权重,以增强研究结果的客观性。
资料来源
本研究所用数据来自 2000~2006年全国食品污染物监测网数据,主要污染物为重金属、农药以及霉菌毒素等,共计 399 033条数据。从中筛选并计算泛长三角五省市大米中的铅、镉、汞、砷等重金属的平均值P50及高端值 P97.5。
原理与方法
1.运用改进层次分析法确定重金属污染因子权重
美国运筹学家 Saaty A.L在 20世纪 70年代提出层次分析法 (analytical hierarchy process,AHP)。在构造判断矩阵时,当因素个数较多时,采用 1~9标度法,由于判断过程中存在复杂性和模糊性,较难一次得到满意 (通过一致性检验)的判断矩阵〔3〕。为此研究人员根据最优传递矩阵的思想对层次分析法进行改进,设计了三标度法,由三标度法可将比较矩阵直接转化为判断矩阵,求出权重值,无须进行一致性检验。三标度法首先构造一个比较矩阵B=(bij)n×n,其中bij表示第i个因素与第j个因素对比的重要性。
r
max/rmin。根据判断矩阵得出最大特征根及其对应的特征向量,进而求出该层内各指标的权重。
2.运用逼近理想解排序法进行综合评价
逼近理想解排序法是系统工程中有限方案多属性决策分析的一种决策技术。其基本原理是:基于归一化后的原始数据矩阵,找出有限方案中的最优方案和最劣方案 (分别用最优向量 A+和最劣向量 A-表示),然后分别计算各评价对象与最优方案的距离和最劣方案间的距离,从而得到各评价对象与最优方案的相对接近程度 Ci值,并以 Ci值的大小为评价优劣的依据〔4-7〕。
(1)构造加权标准化矩阵
利用改进的层次分析法确定的权重和规范化决策矩阵,构造加权标准化矩阵:


(6)按相对接近度大小排序,Ci越大,表明第 i个评价单元越接近最优水平。
实例与分析
1.本文主要讨论对大米污染比较严重的铅、镉、汞、砷四种重金属元素。在利用三标度法构造比较矩阵 B时,依据《中华人民共和国国家标准 》〔8〕(表 1)中重金属污染物在粮食作物中的限量值定义Bij。
(5)计算各评价单元与最优值的相对接近度-

表 1 中华人民共和国国家标准 (m g·kg-1)

利用构造的比较矩阵 Bij,根据公式 (2),求出判断矩阵 C,如式 (10):

由判断矩阵 Cij求解 4种重金属元素的最大特征值、特征向量,并进行一致性检验,检验通过后,特征向量标准化即为 4种重金属元素的权重。根据改进的层次分析法,Pb、Cd、Hg、A s等 4种重金属污染元素的权重为 =(0.0800,0.0800,0.5709,0.2691)。
将本文基于改进层次分析方法求得的 wi与文献中改进模糊数学法〔9〕两个样点的 wi和层次分析法〔10〕得到的wi作比较如表 2。由于文献中所取重金属元素不一致,本文仅对不同方法中重金属权重相对大小作一比较。《中华人民共和国国家标准》(GB 2715—2005)规定的重金属污染物限量 Cd与 Pb的限量值相等均为 0.2 m g·kg-1,根据该标准计算 Cd与 Pb的权重相等,反映了粮食卫生标准中确定的 Cd与 Pb相对与人类毒性相当的特性,与其他方法确定的重金属的权重相比,本文方法得出的权重更加真实可靠。
2.从 2000~2006年全国食品污染物监测网数据中计算泛长三角五省市大米中的铅、镉、汞、砷等重金属的平均值 P50及高端值 P97.5分别如下:
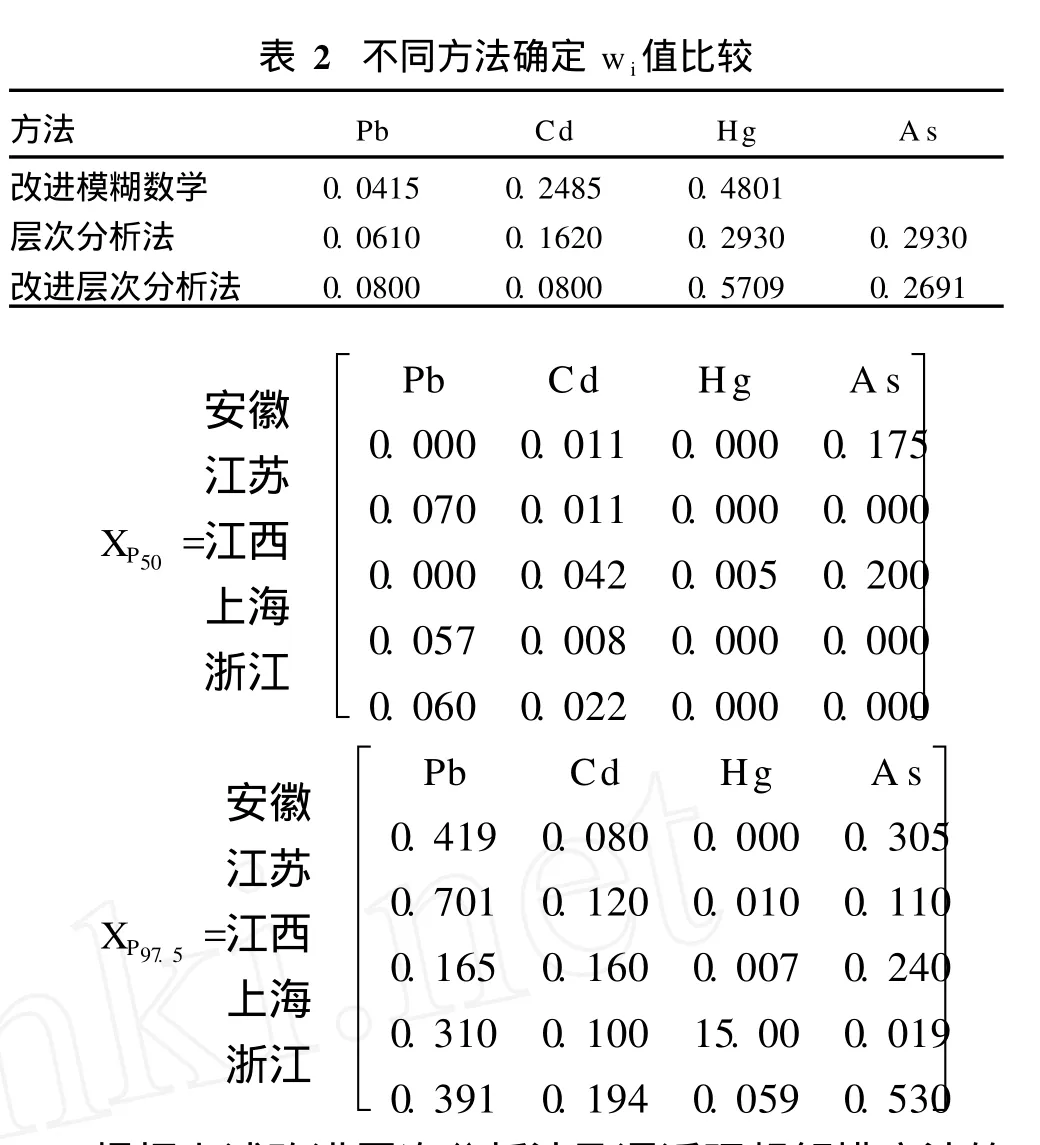
i方法 P b C d H g A s改进模糊数学 0.0 4 1 5 0.2 4 8 5 0.4 8 0 1层次分析法 0.0 6 1 0 0.1 6 2 0 0.2 9 3 0 0.2 9 3 0改进层次分析法 0.0 8 0 0 0.0 8 0 0 0.5 7 0 9 0.2 6 9 1 X P 50=安徽江苏江西上海浙江P b C d H g A s 0.0 0 0 0.0 1 1 0.0 0 0 0.1 7 5 0.0 7 0 0.0 1 1 0.0 0 0 0.0 0 0 0.0 0 0 0.0 4 2 0.0 0 5 0.2 0 0 0.0 5 7 0.0 0 8 0.0 0 0 0.0 0 0 0.0 6 0 0.0 2 2 0.0 0 0 0.0 0 0 X P 97.5=安徽江苏江西上海浙江P b C d H g A s 0.4 1 9 0.0 8 0 0.0 0 0 0.3 0 5 0.7 0 1 0.1 2 0 0.0 1 0 0.1 1 0 0.1 6 5 0.1 6 0 0.0 0 7 0.2 4 0 0.3 1 0 0.1 0 0 1 5.0 0 0.0 1 9 0.3 9 1 0.1 9 4 0.0 5 9 0.5 3 0
根据上述改进层次分析法及逼近理想解排序法的计算方法,运用统计分析软件 SAS9.1进行编程计算,得出结果见表 3。

表 3 2000~2006年泛长三角五省市大米中重金属污染逼近理想解排序法分析结果
讨 论
1.逼近理想解排序法是系统工程中有限方案多目标决策分析中的一种常用方法,对数据分布类型、样本含量无特殊要求,操作简单灵活,信息利用充分,能够很好地对评价对象进行排序,且结果量化准确直观,其局限是无法对所研究对象赋予权重〔9〕。而改进的层次分析法正好弥补了这一缺陷,并且与其他权重赋予方法相比,更加合理可靠。
2.本研究通过改进层次分析法和逼近理想解排序法结合,按照 P50及 P97.5对泛长三角五省市大米中重金属污染情况分别进行综合排序。根据表 3可以看出,按照平均值 P50的逼近理想解排序法结果进行排序依次为江西、安徽、浙江、江苏、上海,而按照高端值 P97.5的结果进行排序依次为上海、浙江、江苏、安徽、江西,由此看见二者的差异是很明显的。通常我们在进行食品安全性评估时常用点估计等方法,此时一般会采用高端值进行分析,导致结果过于保守。通过本次研究我们可以看出,采用平均值和高端值分别进行评估时差别很大,因此在进行食品安全性评估时应慎重选择合适指标,使评估更加合理。
3.逼近理想解排序法容易受到极端值的影响,在本次研究中,经数据核查,排除了异常值后,上海市大米中汞的 P97.5值为 15,远远高于其他省市的值,在一定程度上影响了研究的结果。如何定量分析极端值对综合评价的影响是一个值得深入探讨的问题。
1.杨居容,查燕,刘虹.污染稻、麦籽实中 Cd,Cu,Pb的分布及其存在形态初探.中国环境科学,1990,19(6):500-504.
2.李杰.重庆市园地土壤重金属污染的初步调查.西南农业大学学报,2004,26(3):322-326.
3.张松滨,宋静.土壤重金属污染的灰色模糊评价.干旱环境监测,
4.Op ricovic,Serafim,Tzeng.Comp rom ise solution by M CDM methods:A comparative analysis of V IKOR and TOPSIS.European Journal of Operational Research,2004,16(156):445-455.
5.任力锋,王一任,孙振球,等.TOPSIS法的改进与比较研究.中国卫生统计,2008,25(1):63-66.
6.杨永利,何钦成,黄亚明.TOPSIS法和 RSR法评价医院综合效益变化的比较研究.中国卫生统计,2008,25(1):56-58.
7.刘世炜,唐姬,王英娣,等.TOPSIS法和 RSR法结合评价城市社区预防保健服务利用满意度.中国卫生统计,2008,25(5):518-521.
8.GB 2715-2005,中国人民共和国国家标准—粮食卫生标准.
9.窦磊,周永章,王旭日,等.针对土壤重金属污染评价的模糊数学模型的改进及应用.土壤通报,2007,38(1):101-105.
10.王祖伟.盐碱荒地农垦生态效应的地球化学过程研究报告,2002.
