地质力学磁力模型试验磁场梯度研究

唐 凯 罗先启 张振华

(三峡大学三峡库区地质灾害教育部重点实验室,湖北宜昌 443002)

由于地质环境复杂,且土体是非线性变形材料,在水利、岩土领域的大型工程设计尚不能完全依赖数值模拟技术,相关的地质模型试验技术一直以来都是作为重要的研究手段.其中以离心机模型试验的研究较为深入、应用也较为广泛[1],但是离心机模型的加速度随着距转动轴的距离而改变,模拟出的力线方向并不相互平行[2],这与重力场的力线均指向同一方向的特点有所区别,故而模拟重力场还存在不足.而本文采用磁场来模拟重力场可以克服这一缺陷,该方法概要论述如下:若将一定质量的物体放置于自然环境下的重力场中,不论物体处于何位置,其受到的重力加速度一般认为是一个恒定矢量,其表现为重力场中的力线满足均匀分布、相互平行且指向同一方向这3个特点.本文提出的地质力学磁力模型试验方法可以使试验材料在试验区域内所受到的外加力场满足上述的3个特点[3],较离心机模型试验模拟出的力线分布更接近于真实重力场中的力线分布.在磁力模型试验中决定试验材料受力大小的一个重要因素就是磁性材料所处环境的背景磁场梯度,而表征该梯度大小的指标如何确定及磁场梯度的均匀性是本文研究的两个问题.

1 磁场梯度指标的确定

磁力模型试验中试验材料的应力水平之所以能较常规试验得到提高,是因为试验材料当中掺合的磁性物质除了受到原本的重力作用外还受到了背景磁场所施加的磁力作用,因此,试验材料的应力是由这两种力叠加之后产生的.若磁力与重力大小之比为n,且方向与重力重合,则合力的大小为原先重力的(1 +n)倍,亦可理解为试验材料受到的合加速度大小相当于(1+n)倍的重力加速度.要得到恒定大小的磁力则需要背景磁场满足一定的条件,以下从磁场力计算公式出发,推导相关的条件.

试验所使用的磁性材料为散体磁性颗粒(以下简称磁粉),磁粉在磁场作用下被磁化,从而受到磁力的作用.其所受的磁场力可以由式(1)表示[4]:

式中,Fα为磁性物质沿α方向上的力(N);μ0为真空磁导率(H/m);M为磁化强度(A/m);H为磁场强度(A/m);∂H/∂α为磁场强度梯度(以下称磁场梯度) (A/m2);V为磁粉体积(m3).

磁力模型试验要求Fα为定值,其为几个相关因素之积:当磁粉未被饱和磁化时,磁化强度M是一个与外磁场强度H相关的变量,如图1所示,受到的磁力随着磁场强度而改变,这不符合试验当中力为恒定量的要求;但是,若将外磁场H增加到足够大时,可使磁粉达到饱和磁化状态,即磁化强度M达到上限值时,则磁粉在磁场环境下受到的磁力才有可能为一定值(可见,磁粉被饱和磁化是试验的必要条件).

将Fα看作定值(即n为定值),当mkg饱和磁化(达到饱和磁化强度Ms,为定值)的磁粉在磁场中受到相当于其n倍重力大小的磁力作用时,有

图1 磁粉磁滞回曲线

可见,磁场梯度∂H/∂α须满足(2)式,其反映的是磁场强度H沿α方向上的变化程度.可知磁场梯度为定值,也就是说,磁场强度H沿α方向上是线性变化的.

对磁粉材料进行M-H滞回曲线测定,如图1所示,所选用磁粉的饱和磁化强度Ms为50e.m.u.(电磁单位).磁粉密度m/V经测定得到,大小为6 372 kg/m3.则有:

可知,若要加n倍重力大小的磁力于磁粉上,则需提供n倍于9.9385A/m2大小的磁场梯度.

从理论上说,在磁粉饱和磁化之后,磁粉受力Fα与∂H/∂α是线性关系,增大磁场梯度值,则试验中的磁力也将增大,故可模拟的地层应力水平也越高.因此可以认为上述得出的磁场梯度值是一个下限值.

2 磁场梯度均匀性的获取方案研究

前面已经指出试验磁场的磁场强度需按线性变化,在磁力模型试验中需设计一个满足该条件的试验磁场.利用通电线圈可以产生磁场,为了获得磁场强度线性变化(即磁场梯度均匀性较好)的磁场需对线圈尺寸、形状等参数进行优化.原本繁杂的磁场强度计算工作如今利用成熟的商业软件即可完成[5].根据所需试验磁场的空间尺寸大小,设定线圈的底部半径为10cm,高度为30cm,将线圈顶部半径作为参数进行试算,将计算得到的试验磁场区域内磁场梯度作为依据选定线圈顶部半径的大小.最终确定线圈顶部半径为25cm为较佳尺寸,线圈形状、尺寸,试验磁场范围如图2所示.

图2 线圈尺寸及试验磁场区域

对线圈上方的试验磁场区内的磁场梯度大小进行分析,以线圈顶面中心点为原点,沿线圈轴线垂直向上为z轴正向,建立柱坐标系.针对单个通电线圈,两个同向电流对接线圈,两个反向电流对接线圈这3种情况,利用ANSYS软件计算得试验磁场区域内的磁场强度值如表1所示.

表1 试验磁场区域内磁场强度值

利用ANSYS软件计算得出以上3种情况下试验磁场区域内磁场强度H的分布情况,如图3所示.其表示的是水平长40 cm,垂直高30 cm的圆柱状试验磁场区域内的磁场强度分布图.这里需要说明的是,磁场强度值会因为改变计算中的电流参数而发生改变,但分布情况还是和图3中所示相同.故图3反映的是磁场在空间中的形态,而不仅仅只是在特定的参数下计算出的数值.

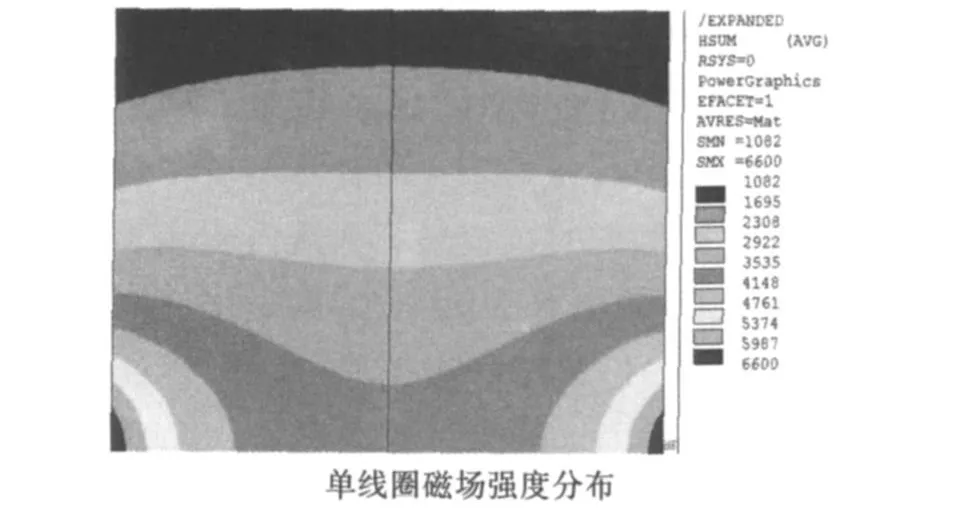
图3 试验磁场区域内磁场强度H分布

由于单线圈情况下的磁场梯度较两线圈对接时较低,特对两线圈对接时的磁场梯度线性进行比较,其结果如图4所示.

图4 磁场梯度值沿z轴方向的变化

根据对几种方案的比较,最终选择以单线圈方案作为磁力模型试验的磁场生成方案.

3 结 论

本文根据磁场力公式及磁性材料特性推导出试验磁场梯度要求,并对线圈产生磁场的梯度均匀性进分析.

(1)磁性材料饱和磁化后,磁场力与外加磁场强度梯度成正比,梯度值越大则模拟的土层应力水平越高.

(2)利用软件计算磁场分布可以方便地通过修改线圈尺寸、形状等参数对磁场强度进行计算,在分析计算结果的基础上对线圈进行优化,可得到梯度线性较好的磁场.

(3)在对单个通电线圈,两个同向电流对接线圈,两个反向电流对接线圈这3种情况的磁场梯度进行分析后发现两个反向电流对接线圈方案生成的磁场梯度线性虽好但磁场区域过于狭小,单线圈方案的磁场梯度虽相对较小但有较大的磁场区域,故可作为模型试验磁场.

[1] 黄志全,王思敬.离心模型试验技术在我国的应用概况[J].岩石力学与工程学报,1998,17(2):199-203.

[2] 包承纲,饶锡保.土工离心模型的试验原理[J].长江科学院院报,1998,15(2):1-7.

[3] 罗先启,葛修润,程圣国等.地质力学磁力模型试验相似材料磁力特性研究[J].岩石力学与工程学报,2008,28 (增2):3801-3807.

[4] 徐建成,徐建民.矿粒所受磁力计算公式的几个问题探讨[J].有色金属,2005,57(1):77-80.

[5] 王世山,王德林,李彦明.大型有限元软件ANSYS在电磁领域的使用[J].高压电器,2002,38(3):27-33.