道路照明阈限亮度差简化计算模型

翁 季,何 荥,黄 珂

（重庆大学 建筑城规学院,重庆 400045）

在机动交通道路照明中,可见度是对驾驶员的视觉可靠性起综合影响作用的评价指标,它对道路照明安全和节能起着非常重要的作用[1]。可见度是人眼辨认物体存在或形状的难易程度,常采用可见度水平表示[2],它表示了目标和背景的亮度差大于其阈限状态时亮度差的倍数：

式中：VL为可见度水平;ΔL为视看目标的亮度与其背景亮度的差,即有ΔL=Lt-Lb;ΔL0为阈限亮度差,视看目标刚刚可见时目标亮度与其背景亮度的差,即：ΔL0=Lt0-Lb。

由上式可知,影响可见度水平的主要因素有目标物亮度、紧邻的背景亮度和阈限亮度差。而阈限亮度差的确定是可见度计算的关键。不同学者针对可见度和阈限亮度差进行了相关研究。Ad rian W等通过阈限亮度实验,得到了阈限亮度差与视角和背景亮度的关系[3];美国道路照明标准RP-8-00根据A drian提出的计算模型,推荐了小目标可见度STV设计标准[4],首次将可见度纳入道路照明设计标准中,是一个里程碑式的研究成果;在此基础上,Cuvalci等研究了可见度计算模型及参数修正[5];Mayeur等研究了小目标可见度在道路驾驶行为中的作用[6];翁季、陈仲林等研究了小目标可见度影响因素及设计方法[7];Gǜler等对可见度的计算值和实测值进行了比较研究[8];蒋宏等提出了小目标可见度计算方法的不足及修正[9];陈文成等探讨了大视野范围内可见度模型的建立及对夜间道路照明设计的指导意义[10]。

上述学者对可见度的研究工作中,其可见度的计算过程,特别是阈限亮度差的计算仍然沿用美国道路照明标准所推荐的计算模型。由于 RP-8-00中阈限亮度差的计算模型非常复杂,为了便于进行道路照明可见度计算,通过阈限亮度实验和韦伯—费昔勒定律,在一定的计算条件下[11],得到具有一定精度的、简化的计算模型。

1 阈限亮度差的基础计算模型

1.1 RP-8-00中阈限亮度实验的基础计算模型

研究表明[12],邻近环境的适应亮度La（目标物背景亮度和等效光幕亮度之和）、目标物呈现的时间长短、观察者年龄和负对比（目标物亮度小于背景亮度）修正是影响阈限亮度差的重要因素。美国道路照明标准推荐的小目标可见度STV设计标准以识别时间为 0.2 s、视角为 7.45′、驾驶员年龄为60岁的不利条件下,依照适应亮度La、视角大小、负对比修正、观察时间修正、观察者年龄修正等因素进行推导,确定了阈限亮度差的计算方法。

在一定的条件下,阈限亮度差ΔL0的大小与不同的人眼适应亮度成正比关系,而与视角大小成反比关系[13],在正对比条件下,RP-8-00采用下式作为ΔL0的基础计算模型：

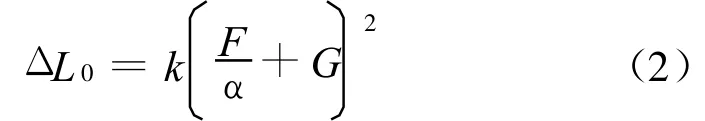
式中k为系数,取k=2.33;α为视角,单位为′;F为人眼适应亮度La的函数,且有F=f1（La）;G为人眼适应亮度La的函数,且有G=f2（La）。

由Ad rian的实验结果,在3段人眼的适应亮度范围内分别给出F和G表达式：

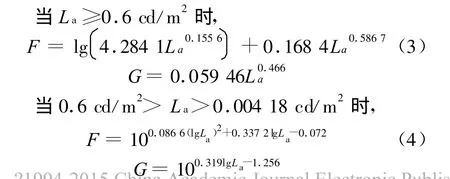
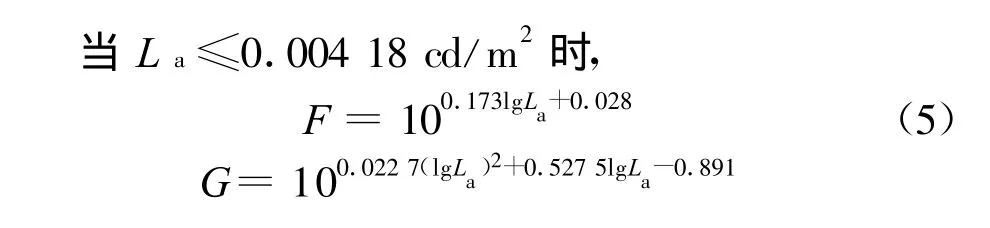
可以看出,RP-8-00中阈限亮度差的计算模型非常复杂,在简化计算模型的研究过程中,为了便于比较,其计算前提与RP-8-00一致。

1.2 以阈限亮度实验推导简化基础计算模型

采用定值刺激法（又可称为强迫选择法）进行阈限对比实验[14]。在进行计算机模拟实验时,观察者的下颚被要求放置在固定支架上,以便固定观察者的眼睛和计算机屏幕之间的正视距离为1 m。同时在支架上放置一个计算机键盘,观察者根据自己的视看结果敲击键盘,输入判断信息。

计算机模拟实验的软件是自编的,它可以使屏幕和不同大小的朗道尔环的亮度独立和自由地调节,朗道尔环的识别时间也可以自由调节,其4个开口方向随机出现,且每个开口方向呈现3次。实验选取年龄在20～30岁、男女各半、视力正常的20个观察者进行了18 000多次观察。观察者适应暗室的环境和熟悉实验过程的各项操作后进行正式测试,由其对朗道尔环开口方向的正误判断得到不同背景亮度、不同识别几率下阈限亮度差的实测值。根据对城市道路的实测,城市机动车交通道路照明路面亮度水平往往在0.75～5.0 cd/m2之间,在此条件下,若视角α恒取7.45′,通过回归拟合的方法得到50%识别几率下阈限亮度差ΔL0与背景亮度Lb之间的关系为：

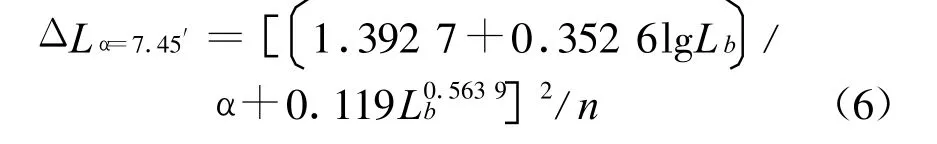
在道路照明中,驾驶员对前方障碍物的识别几率应该接近100%,否则就会出现事故。而通过人眼阈限对比实验结果而拟合成的（6）式对应的识别几率仅为50%,但是由于实验是无法直接得到识别几率接近100%时的值。根据对人眼阈限对比实验结果进行分析后表明,在相同背景亮度和视角下,不同识别几率的阈限亮度差之间的比例为常数K[15]。

实验与RP-8-00相同取K为2.6。于是在城市机动车交通道路照明范围内,视背景亮度为适应亮度,用下式表示道路照明小目标可见度计算中要求的阈限亮度差：

式中：La为人眼适应亮度;n为实验方法调整系数,n=3.34;

表1为式（2）与式（7）计算结果的比较,可以看出,二式的计算结果非常接近,相对误差均处在-1.25%～+1.47%之间。由于阈限亮度差常小于背景亮度的1%,考虑测试系统误差的因素,可认为公式（7）是可靠的,由于RP-8-00标准中规定视角恒为7.45′,因此式（7）是一个非常实用、具有一定精度的、简化的阈限亮度差计算模型。

表1 阈限亮度实验的计算模型与RP-8-00的计算模型比较

1.3 以韦伯—费昔勒定律推导简化基础计算模型

韦伯—费昔勒定律是一项著名的心理学定律,即当人们受到某种刺激时,其反应的感觉程度与该刺激的大小之间的关系可用定量表示出来,实际上这是确定主观感觉量与客观物理量之间的内在关系,即确定定性与定量之间的关系。用公式表示如下：

通常把（8）式称为古典的韦伯—费昔勒定律,可成功地确定一些物理刺激量与感觉量之间的关系。但在实际研究中发现,有些定性与定量之间的问题却不能利用古典的韦伯—费昔勒定律得到合理的解决。特别在道路照明工程中,人的视觉行为反应已不是在物理刺激量与感觉量的范围内能研究的问题,而是要受到人的经验、知识等与光感觉的综合影响,故在研究人的主观反应时,应对古典的韦伯—费昔勒定律加以进一步完善,使之也能适应于照明工程的实际情况。研究得到了应用于照明工程中的广义韦伯—费昔勒定律公式[16]。

从表1看出,在城市机动车交通道路照明亮度水平范围内,阈限亮度差是随着人眼适应亮度增大而成比例增大,利用广义韦伯 —费昔勒定律进行回归分析,若将适应亮度La视为光对人眼的刺激量,阈限亮度差ΔL0视为对应于光刺激量的视知觉量,当视角α为7.45′时,可以求出人眼适应亮度在0.75～5.00 cd/m2范围内,阈限亮度差ΔL0与人眼适应亮度La之间关系式如下式所示：

式中：Lamax为适应亮度La的最大值,式中取5 cd/m2。

上式的判定系数为0.999,上式的计算结果与表2中式（2）的ΔL0比较几乎完全一致,相对误差均处在-0.18%～+0.31%,一方面说明了阈限亮度差与人眼适应亮度之间的关系完全符合广义韦伯—费昔勒定律,同时也说明了广义韦伯—费昔勒定律推导出的公式（9）符合国外学者的研究结果。采用式（9）将大大简化可见度的计算过程。

表2 用韦伯—费昔勒定律推导的计算模型与RP-8-00的计算模型比较

2 阈限亮度差的修正系数

2.1 负对比修正系数K f

在实际的道路照明条件下,常常会发生亮背景上观察暗目标,即驾驶员看到的目标会呈现出较黑暗的剪影状。视觉实验表明,在相同△L的时候,负对比情况下的目标物要比正对比时更容易察觉,由于式（2）是在正对比条件下得到的,所以要对阈限亮度差进行负对比修正。

负对比修正系数（Kf）由适应亮度La和视角α决定,并在3个不同的人眼适应亮度范围内分别给出：

当La≥0.1 cd/m2时,

当La≤0.003 981 cd/m2时,

K f=0.5

根据RP-8-00中计算负对比修正系数Kf的数学模型,负对比修正系数是随着人眼适应亮度增大而略有增大,利用广义韦伯—费昔勒定律进行回归分析,将适应亮度La视为光对人眼的刺激量,负对比修正系数Kf视为对应于光刺激量的视知觉量,当视角α为7.45′时,可以求出人眼适应亮度在0.75～5.00 cd/m2范围内,负对比修正系数Kf与人眼适应亮度La之间关系式：

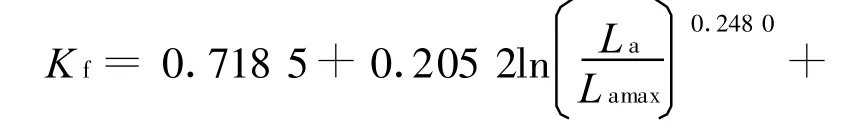
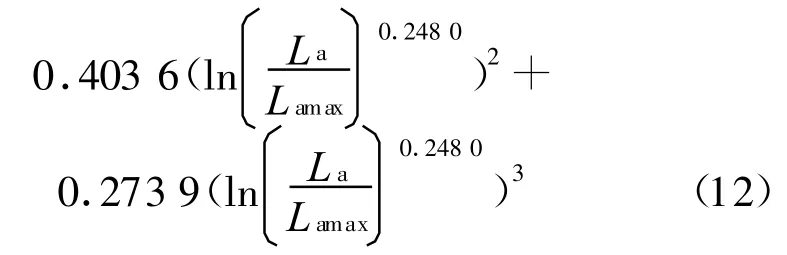
式中：Lamax为适应亮度La的最大值,该式取5 cd/m2。式（12）的判定系数为0.999,其计算结果与表3中RP-8-00中Kf（式10）的计算值非常一致,相对误差均处在-0.03%～+0.01%,说明了负对比修正系数与人眼适应亮度之间的关系完全符合广义韦伯—费昔勒定律,且采用式（12）可以简化道路照明计算。

表3 不同负对比修正系数计算模型的比较

2.2 识别时间修正系数K t

当道路情况复杂且行驶速度很快时,观察时间越短对目标的分辨力就越差。良好的可见度水平应使司机在很短的时间内观察到障碍物,以便随机应对。由于式（2）的计算模型的数据是根据2 s或无限制识别时间得到的[4]。为了在较短时间识别目标物,△L需要提高。为此须进行观察时间的修正。若取t=0.2 s,由视觉实验得出观察时间的修正系数K t与视角、人眼适应亮度的关系,RP-8-00用下式表示：

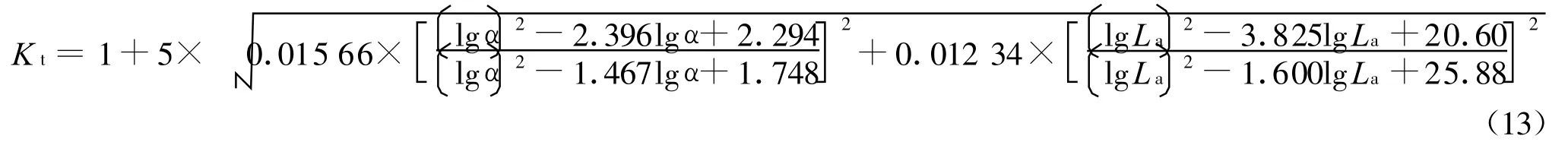
根据该计算模型,为简化计算,可利用古典韦伯—费昔勒定律进行回归分析。将适应亮度Lb视为光对人眼的刺激量,时间修正系数Kt视为对应于光刺激量的视知觉量,当视角α为7.45′,观察时间t=0.2 s时,可以求出人眼适应亮度在 0.75～5.00 cd/m2范围内,识别时间修正系数Kt与人眼适应亮度La之间关系式如下式所示：

式（14）的判定系数为0.999,其计算结果与表4中RP-8-00中Kt的计算值比较非常一致,相对误差均处在-0.04%～+0.01%,说明了时间修正系数与人眼适应亮度之间的关系同样符合韦伯—费昔勒定律。所以按美国道路照明标准条件进行照明计算时,完全可以用（14）式来计算识别时间修正系数Kt。

表4 不同识别时间修正系数计算模型的比较

2.3 年龄修正系数Ka

人眼随着年龄增长,角膜和水晶体逐渐变黄,瞳孔收缩功能也会减弱,60岁时人眼对光的感受只有20岁时的33%。美国道路照明标准是以识别时间为0.2 s、60岁老年驾驶员的不利条件给出小目标可见度标准建议值。由RP-8-00给出的年龄修正系数表达式中算得年龄修正系数Ka为1.768 2。

于是,基础计算模型经修正后的阈限亮度差为：

3 3种方法计算可见度水平的比较

采用2种方法简化阈限亮度差的计算过程,第1种方法是以 RP-8-00的计算模型为基础,通过韦伯—费昔勒定律对其计算结果进行回归分析,提出了简化公式;第2种方法是以阈限亮度实验得到的计算模型为基础提出了简化公式,根据式（7）,在人眼适应亮度0.75～5.00 cd/m2范围内,识别时间为0.2 s、视角为 7.45′、60 岁的阈限亮度差,即经过识别时间修正、年龄修正和负对比修正后的阈限亮度差为：

式中：La为人眼适应亮度,cd/m2;Kf为负对比修正系数,由（12）式确定,正对比时取Kf为1。

比较RP-8-00推荐的计算方法和该文采用的2种简化方法计算可见度水平,假定某目标物与其背景亮度差 ΔL恒为-0.5 cd/m2,其它条件不变,根据式（1）,用3种方法计算目标物的可见度水平,其结果见表5。改变ΔL,其误差不变。

表5 采用3种计算模型计算的可见度水平结果比较

从表5看出,第1种方法的计算结果相对误差处在-0.26%～+0.10%;第2种方法相对误差处在-1.4%～+1.22%,采用上述2种计算方法均可得到具有较高精度、简化的阈限亮度差计算模型。

4 结论

通过利用阈限亮度实验和韦伯—费昔勒定律对阈限亮度差计算模型的研究分析,可得到如下结论：

1）利用阈限亮度实验得到的阈限亮度差的计算模型符合韦伯—费昔勒定律,因此得到的可见度能确切地反映出人们视感觉的整体效果。

2）利用根据阈限对比实验和韦伯—费昔勒定律得到的简化阈限亮度差计算模型计算道路照明可见度,其结果与利用RP-8-00中的阈限亮度差计算模型计算得到的可见度值比较吻合,这2个简化阈限亮度差计算模型能满足道路照明可见度计算需要。

[1]LEW IS I.Lumen effectiveness multip liers for outdoor lighting design[J].Journal o f the Illuminating Engineering Society,2001（2）：40-52

[2]JR柯顿,A M 马斯登.光源与照明[M].4版.陈大华,译.上海：复旦大学出版社,2000.

[3]ADRIAN W.V isibitity of targets：model for calculation[J].Ligh ting Research and Techno logy,1989（4）：26-31

[4]The Standard Prac tice Subcomm ittee of the IESNA Roadw ay Ligh ting Comm ittee.RP-8-00 Roadw ay Ligh ting[S].ANSI/IESNA,2000

[5]OLKAN CUVALCI,BUGRA ERTAS.Roadw ay Ligh ting Design Methodology and Eva luation[C]//2000 Society for Design and Process Science Printed in the United States of America.

[6]ANA IS MAYEUR, ROLAND BREMOND,CHRISTIAN BASTIEN JM.The effect of the d riving activity on targetdetection as a function of the visibility level：Implications for road lighting[J].Transportation Research Part F：Traffic Psychology and Behaviour,2010（2）：115-128

[7]翁季,陈仲林,刘波,等.城区道路照明可见度研究[J].照明工程学报,2005（1）：20-22

WENG JI,CHEN ZHONG-LIN,LIU BO,et a l.Study on the visibility of the urban road lighting[J].China Illum inating Engineering Journal,2005（1）：20-22.

[8]ONDER GULER,SERM IN ONAYGIL.Evaluation of visibility level formu la in road lighting w ith field measurements[C]//Proceedings of Third International Conference on Electrical and Electronics Engineering,ELECO'2003,Bursa,Turkey,December 3-7,2003.

[9]蒋宏,潘晓东,林炳淦.道路照明可见度研究[J].交通科技与经济,2006（6）：6-8

JIANG HONG,PAN XIAO-DONG,LIN BING-GAN.A study of the visibility of roadw ay lighting[J].Technology&Economy in A reas of Communications,2006（6）：6-8

[10]陈文成,林燕丹,陈大华.可见度模型的探讨及其在道路照明中的应用[J].复旦学报：自然科学版,2005,44（4）：571-577.

CHEN WEN-CHENG,LIN YAN-DAN,CHEN DAHUA.Study on modeling visibility and its application in road lighting[J].Journal of Fudan University：Natural Science,2005,44（4）：571-577.

[11]CIE 140-2000 Road Lighting Calcu lations[R].Vienna：CIECentral Bureau,2000.

[12]ADRIAN W.Fundamentals of roadway lighting[J].Light&Engineering,2004,12（2）：57-71.

[13]NARISADA K.Revealing pow er and road lighting design[C]//The 18th Biennial Transportation Research Board Visibility Symposium.17-19 Ap r,2007,Texas,USA

[14]NANA ITOH,KEN SAGAWA.V isual p roperty of people with low vision（2）：Contrast sensitivity function[C]//26thSession of the CIE.4-11 July 2007,Beijing：D1-107～D1-110

[15]ZHANG SHENG-PENG,CHEN ZHONG-LIN.App lication threshold brightness contrast experiments of human eyes for study on the visibility[C]//26thSession of the CIE.4-11 July,2007,Beijing：D1-66～D1-69

[16]陈仲林,翁季,胡英奎,等.照明工程中定性与定量之间的转换研究[J].重庆建筑大学学报,2006（4）：1-3.

CHEN ZHONG-LIN,WENG JI,HU YING-KU I,et al.Study of transform between qualitative analysis and quantitative analysis in lighting engineering[J].Journal of Chongqing Jianzhu University,2006（4）：1-3.

（编辑胡英奎）