双断级滑行艇的阻力回归公式

沈小红 吴启锐 肖 笛 邓爱民

中国舰船研究设计中心，湖北 武 汉 430064

双断级滑行艇的阻力回归公式

沈小红 吴启锐 肖 笛 邓爱民

中国舰船研究设计中心，湖北 武 汉 430064

本文以5艘双断级滑行艇模型的试验数据为基础，采用多元线性回归的方法对试验数据进行回归分析，从而导出在不同断级参数情况下双断级滑行艇的阻力回归公式。通过相对误差分析法验证了回归公式的精确性，并根据回归的结果绘制成图以供设计参考。

双断级滑行艇；多元线性回归；阻力回归公式；相对误差分析法

1 引言

双断级滑行艇的主要优点是航速高、阻力小，而两个断级的几何参数（断级的纵向位置和高度）对其阻力性能的影响至关重要，由于各滑行面之间的干扰比较复杂［1］，因而断级的确定主要还是依靠模型试验，至今尚无一种有效的理论计算方法。本文将根据模型试验所得到的试验数据，用多项式回归的方法［2－3］得到在不同断级参数情况下双断级滑行艇的阻力公式。

本文将取5艘双断级滑行艇模型的试验数据进行回归分析，除了断级参数以外，这些模型的主尺度完全相同。这些模型的编号及断级参数值如表1所示。

表中，l1为断级总长度；θ1为断级角度 （任何纵剖线上两个断级下缘点与艇尾封板下缘点的连线在一条直线上［4］，此直线与基线的夹角即为断级角度）；l2为前断级长度；l3为后断级长度；h为断级高度（两个断级高度相等）。通过断级总长度l1和断级角度θ1这两个因素应用几何关系可求出前断级长度l2、后断级长度l3和断级高度h的值，这样就能将双断级艇的断级参数从3个因素的变化转化为两个因素的变化。因此，本文所选取的试验模型的断级参数就是由断级总长度l1和断级角度θ1这两个因素来确定的。

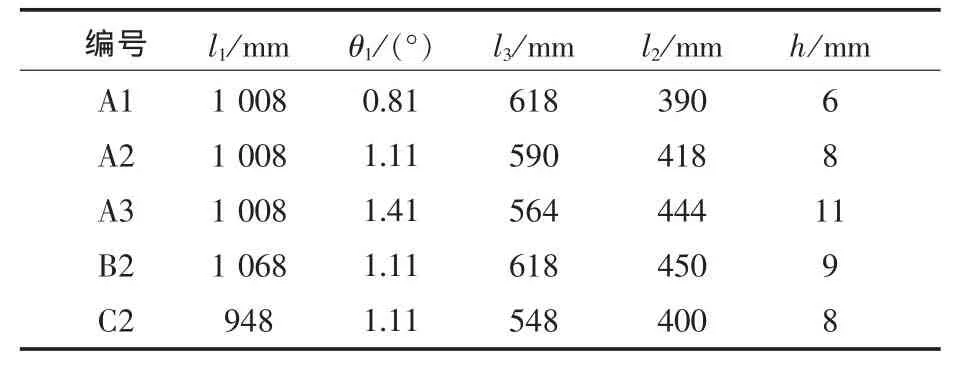
表1 模型的编号及对应的断级参数值

2 多元线性回归

设随机变量y与非随机变量之间有如下的p元线性回归模型：

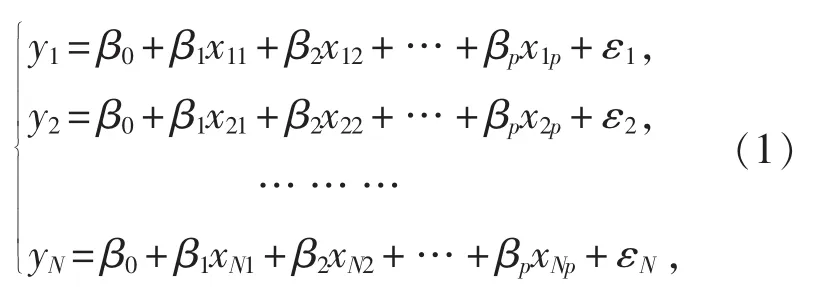
式中，β0、 β1、 …、 βp是p＋1 个待估参数；x1、 x2、…、xp是p个可以精确测量或可控制的一般变量；ε1、 ε2、…、 εN是 N 个相互独立且服从同一正态分布N（0，σ）的随机变量。这就是多元线性回归的数学模型［5］。

采用最小二乘估计法可求出系数β0、β1、…和βp，而后可确定 y 与 x1、 x2、…、 xp之间的关系为：

y＝β0＋β1x1＋ β2x2＋ …＋ βpxp（2）

在上述过程中，尚需讨论两个方面的问题：一方面是线性相关关系的假设检验，以验证y与x1、x2、…、xp之间确实存在线性关系；另一方面是回归系数的假检验，以验证每个因子x1、x2、…、xp对y的影响程度，剔除那些影响不显著的因子，这就需要选择“最优”的回归方程［6］。

所谓“最优”回归方程，就是包含所有对y影响显著的变量而不包含对y影响不显著的变量的回归方程。选择“最优”回归方程的方法有几种，本文将采用逐步回归分析的方法来建立“最优”回归方程。

逐步回归分析的基本思想是将因子逐个引入。引入因子的条件是，该因子的偏回归平方和经检验是显著的。同时，每引入一个新因子后，要对旧因子逐个检验，将偏回归平方和变为不显著的因子剔除。采用上述方法，由于每一步都进行检验，因而保证了最后所得的方程中所有的因子都是显著的。

3 双断级滑行艇的阻力回归公式

下面将模型A1、A2和A3（这些模型具有相同的断级总长度l1）作为一组进行回归，再将模型A2、B2和C2（这些模型具有相同的断级夹角θ1）作为一组进行回归。

3.1 A1、A2 和 A3 阻力回归公式

在回归分析前，首先要将因变量和所有自变量进行无因次化［7］，各变量无因次化结果如下：

阻力无因次化：阻升比R／Δ；重心无因次化：xg／B（B为折角线平均宽度）；断级长度 l1无因次化：l1／B。

断级夹角θ1在实艇和模型中具有相同的角度，它们的几何关系不会发生变化，故断级夹角θ1无需进行无因次化。

以断级夹角θ1、xg／B和动负荷系数CB为自变量，阻升比R／Δ为因变量，进行三元多项式回归分析［8］，这样可以把阻升比R／Δ的试验数据在断级夹角θ1、xg／B和动负荷系数CB3个方向上进行光顺。故可设回归多项式的表达式如下：

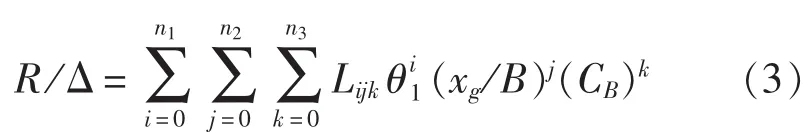
从绘出的试验点草图可以看出试验曲线比较平缓，没有出现拐点，则可取 n1＝n2＝n3＝2，即可将式（3）转化为：

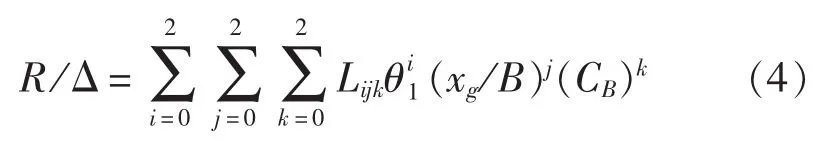
显然，式（4）为一非线性表达式，为了能应用回归的方法进行处理，可以采用变量替换的方法将其转化为多元线性回归表达式［9］。

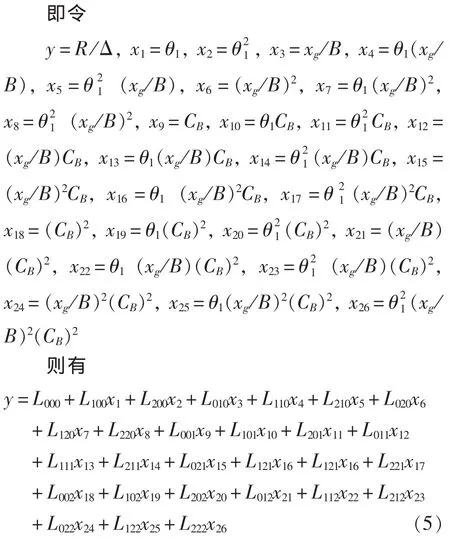
本文所取试验数据为：断级夹角θ1取0.81°、1.11°、1.41°等 3 个值； xg／B 取 1.062 5、1.125 0、1.187 5 等 3 个值；动负荷系数 CB取 0.030 16、0.032 18、0.033 42、0.034 19、0.035 65、0.037 88、0.039 89、0.042 55、0.045 21、0.047 48、0.050 64、0.053 81、0.057 44、0.061 27、0.065 10 等 15 个值。形成的阻升比数据如表2所示。

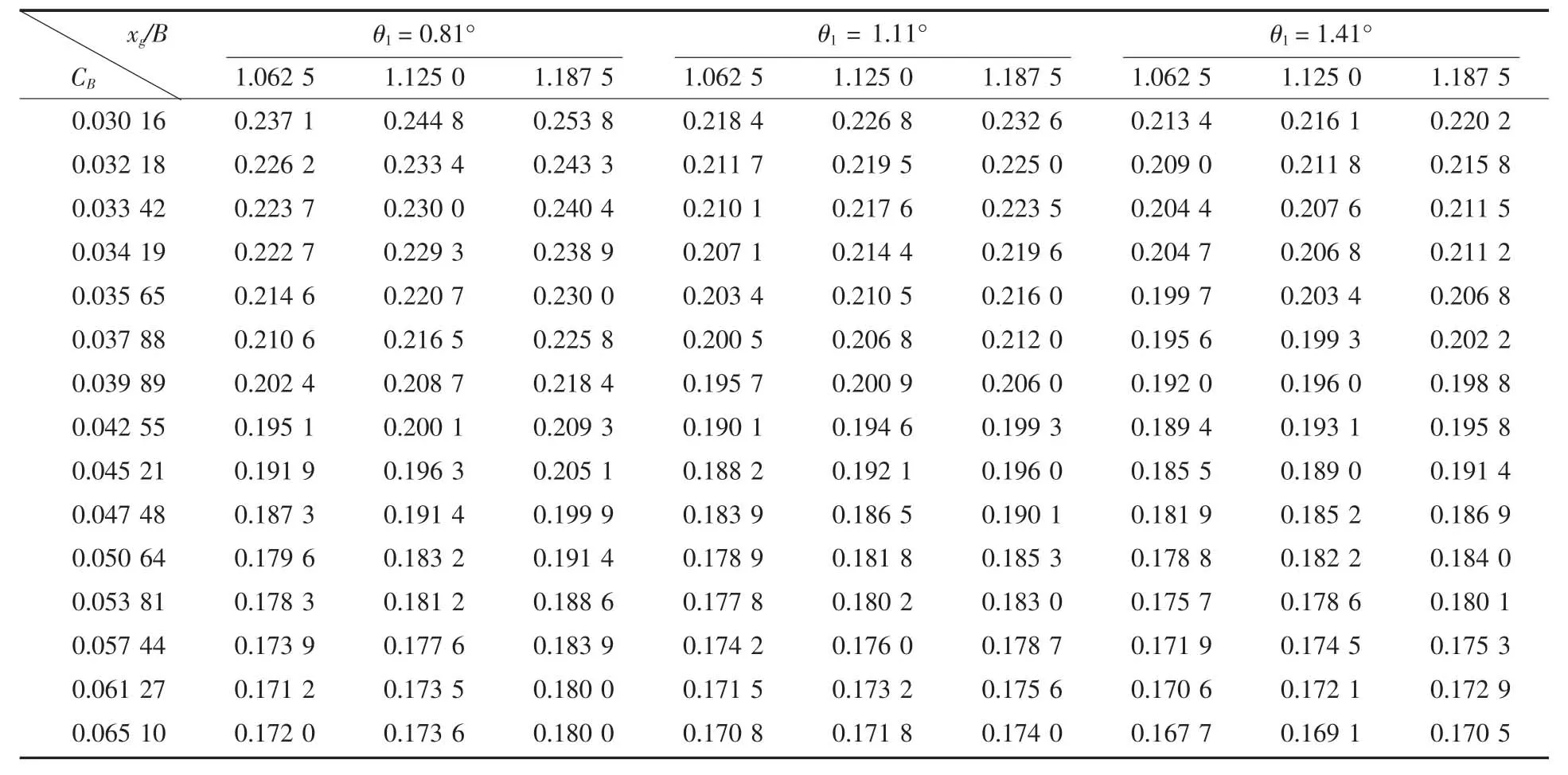
表2 A1、A2和A3阻升比R／Δ 数据

根据逐步回归的计算方法，应用Matlab编程计算可算得显著变量回归系数Lijk的值，其具体结果如表3。

表3 A1、A2和A3阻升比R／Δ 计算公式的Lijk值

3.2 A2、B2 和 C2 阻力回归公式

按照回归A1、A2和A3阻力公式的方法，同样可以对A2、B2和C2阻力公式进行回归，故可设其回归多项式的表达式为：

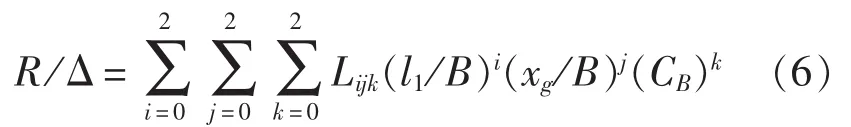
采用变量替换的方法将式（6）转化为多元线性回归表达式的方法同上节内容，故在此不再赘述。 在本节所取的试验数据中，l1／B 取 1.481 25、1.575 0、1.668 75 等 3 个值；xg／B 和动负荷系数 CB所取的值同上一节。同样也形成了个数据，其阻升比R／Δ的数据如表4所示，应用Matlab编程计算所得的阻升比R／Δ计算公式的Lijk值如表5所示。

4 计算公式精确性分析

对于以上回归的阻升比计算公式，还应分析其精确性。本文将采用相对误差分析法［10］，从两个方面来验证以上回归公式的精确性。首先从进行回归的试验数据中取出原始数据进行比较 （由于试验数据太多，故只取小部分数据进行比较验证），其比较结果如表6和表7所示；其次，由于模型 A3 在重心纵向位置 xg＝640 mm（即 xg／B＝1.0）时的试验数据并没有参加回归，则可用此试验数据与回归公式计算结果进行比较，其比较结果如表8所示。

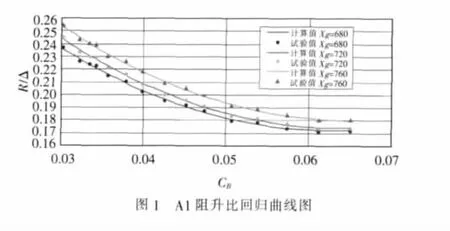
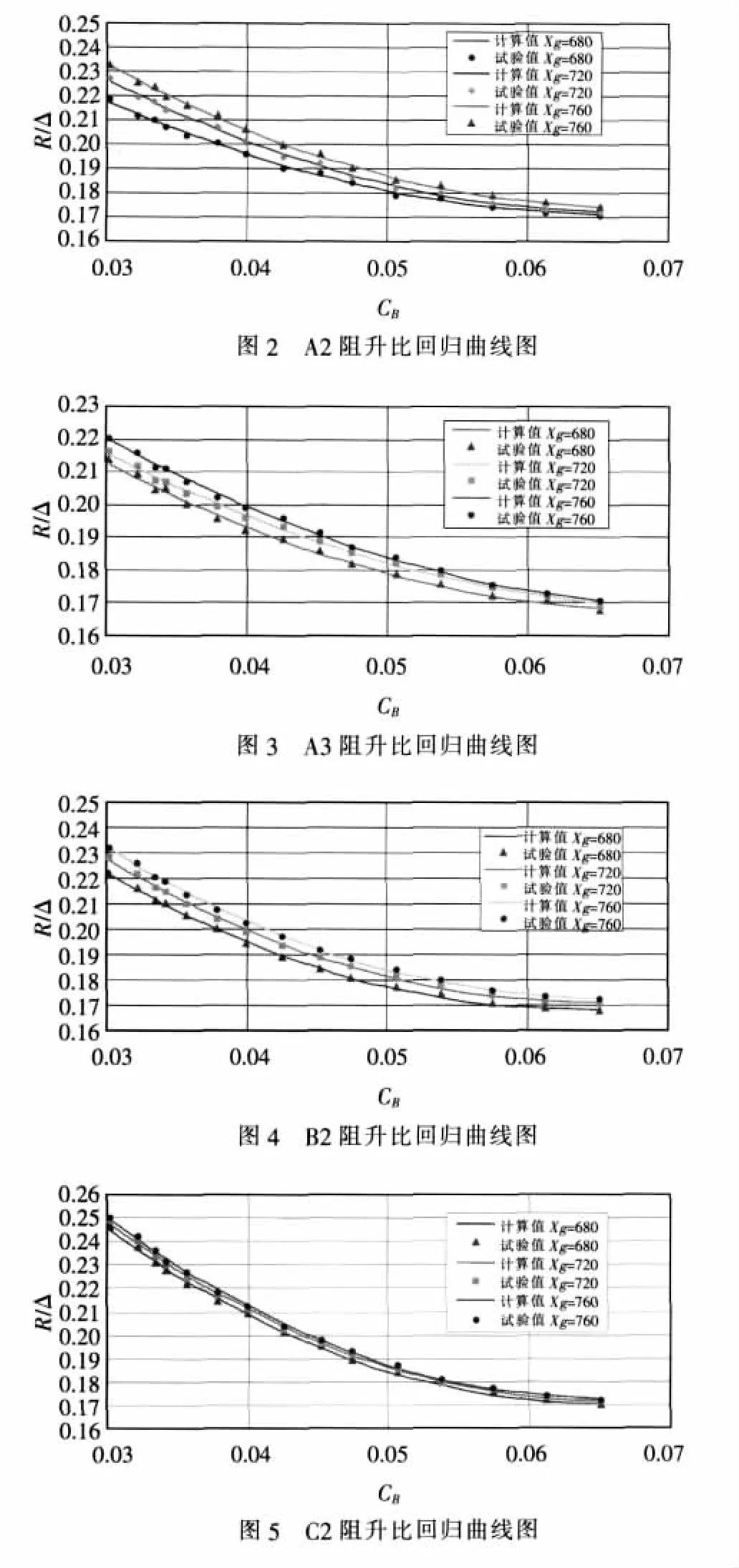
由以上分析结果可见，根据回归计算公式所求得结果与原始试验值非常接近。此外，如图1～5所示，回归曲线与试验数值点具有良好的贴近性，由此，可以看出本文的回归公式计算精度比较高。

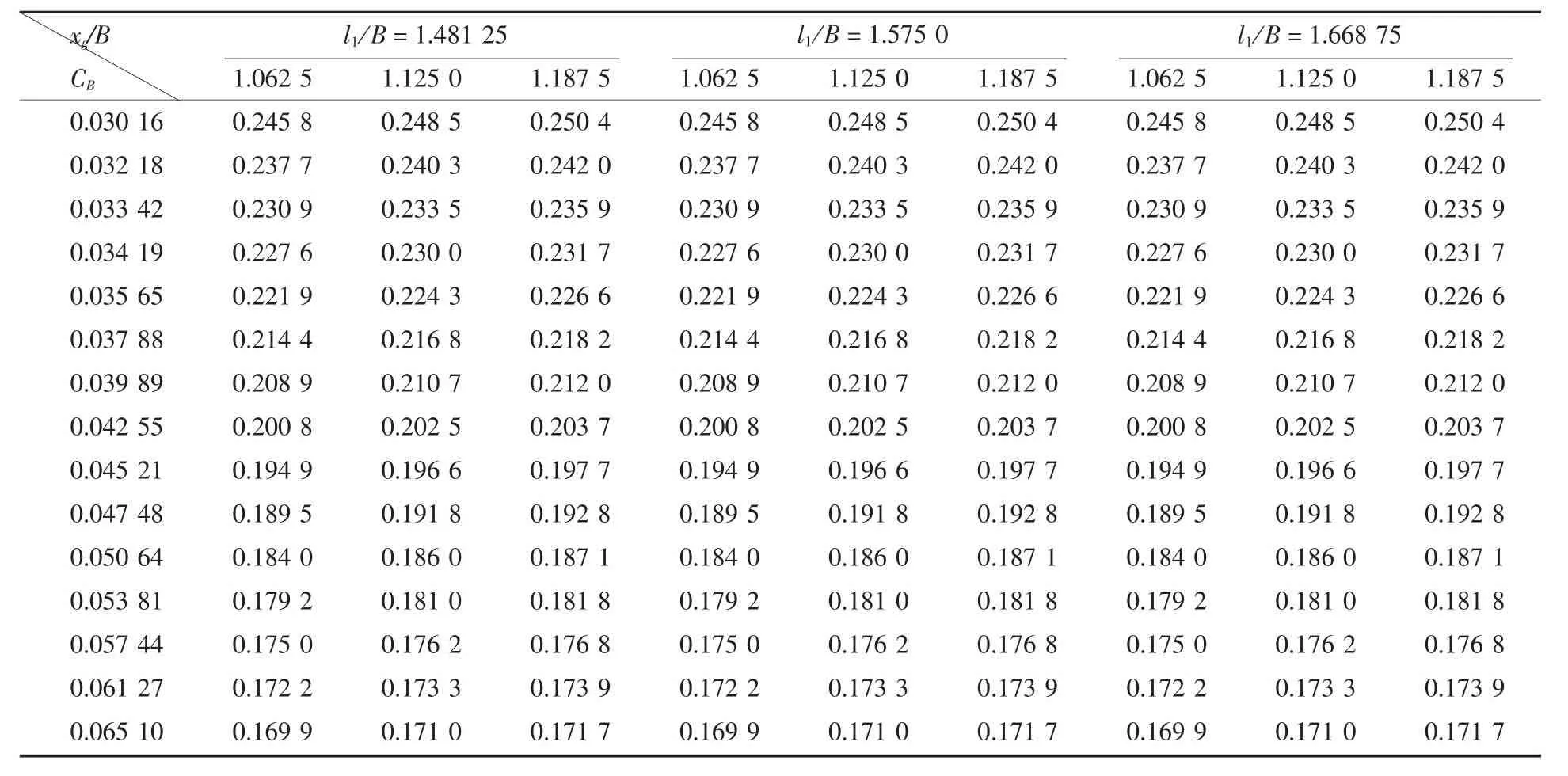
表4 A2、B2和C2阻升比R／Δ 数据

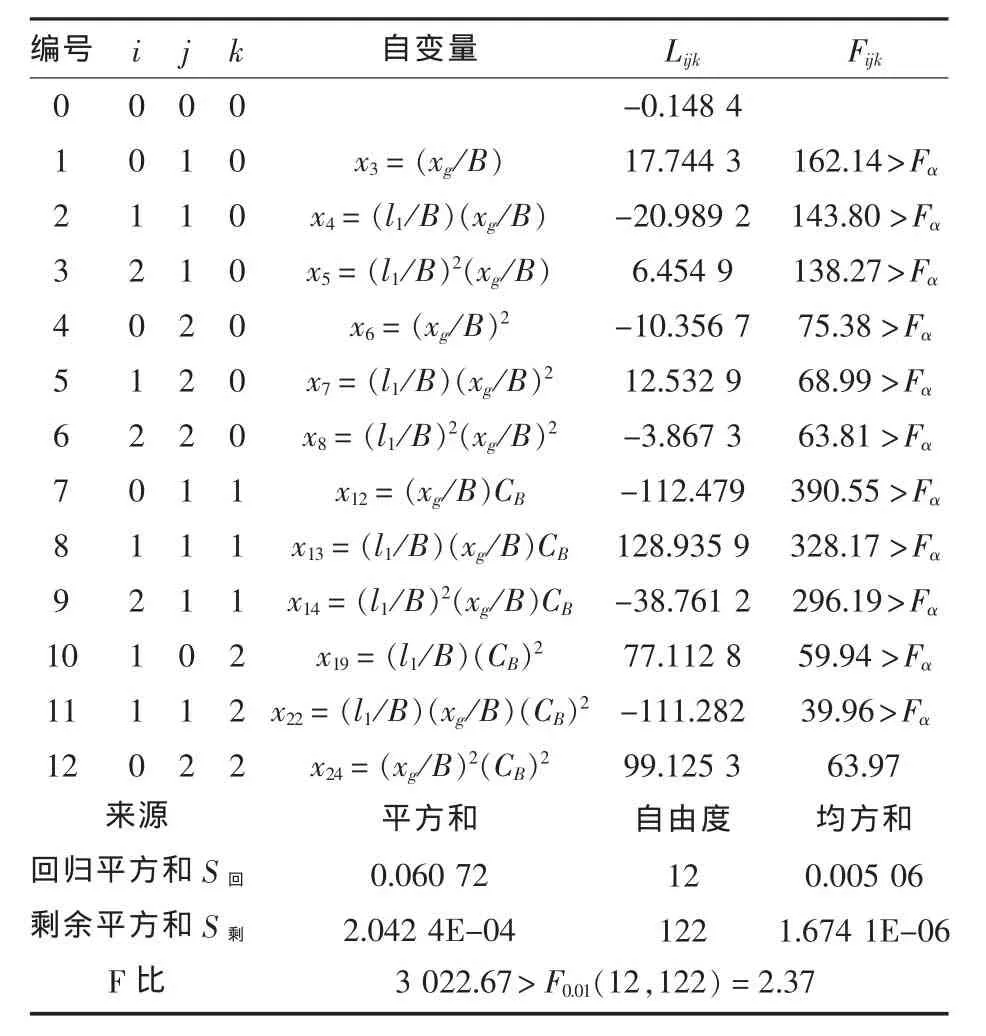
表5 A2、B2和C2阻升比R／Δ 计算公式的Lijk值

表 6 A1、A2 和 A3 在 xg／B ＝ 1.575 时比较结果

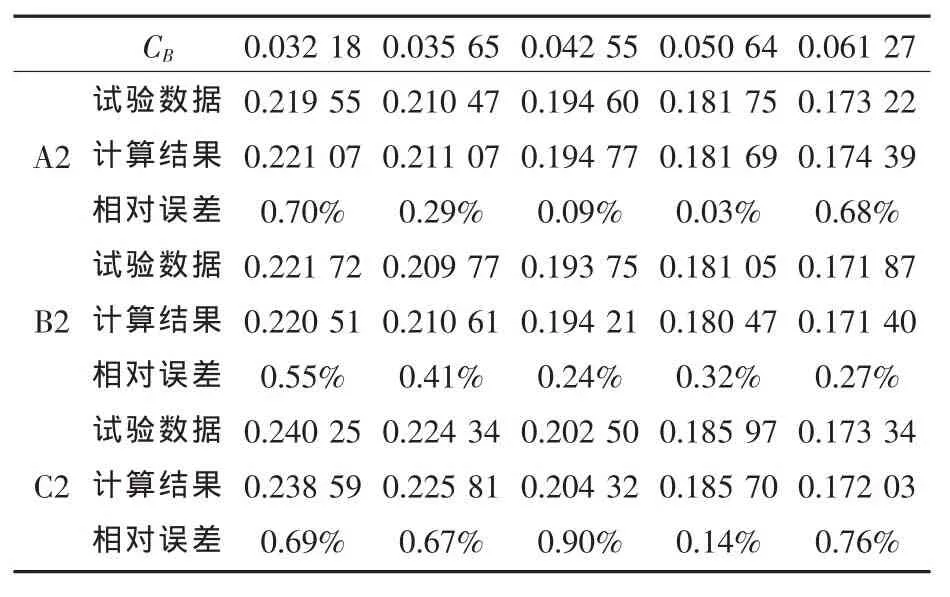
表 7 A2、B2 和 C2 在 xg／B ＝ 1.575 时比较结果

表 8 A3 在 xg／B＝1.0 时比较结果

5 结 论

本文采用多元线性回归中逐步回归的计算方法，得出双断级滑行艇在不同断级参数下的 “最优”阻力回归公式，通过对计算值与试验值的相对误差分析，可以看出回归所得的计算公式精度比较高，从而证明了根据试验数据，采用回归分析的方法得出双断级滑行艇的阻力计算公式是有效而可信的。本文所得的回归公式可以为设计双断级滑行艇的断级参数选择提供一些理论依据。

［1］董祖舜.快艇动力学［M］.武汉：华中理工大学出版社出版，1991，4.

［2］周连第.多元回归分析方法及在船舶科研设计中的应用［M］.北京：国防工业出版社，1979.

［3］谭仲楷.应用回归分析方法估算圆艇舭阻力［J］.中国造船，1979，67（2）：14－29.

［4］夏翔.超高速断级滑行艇推进系统工况配合特性的研究［J］.中国舰船研究，2008，3（2）：39－42.

［5］上海师范大学数学系.回归分析及其试验设计 ［M］.上海：上海教育出版社，1978.

［6］何志飞，邢圣德.滑行艇之最佳阻力［J］.江苏船舶，1996，13（4）：1－4.

［7］郭亨翔，倪家俊，张蓓玉.当今世界优秀船型主要参数的回归分析［J］.船舶设计通讯，2002（4）：12－31.

［8］ LAMMEREN W P A VAN，MANEN J D VAN，OOSTERVELD M W C.The wageningen B－screw series Trans［J］.Society of Naval Architects and Marine Engineer，1969（77）.

［9］陈宾康，赵成璧，洪安祥.船用组合舵水动力系数的回归公式［J］.中国造船，1999，147（4）20－27.

［10］李红.数值分析［M］.武汉：华中科技大学出版社，2003.

A Resistance Regression Formula for Double－stepped Planing Craft

Shen Xiao－hong Wu Qi－ruiXiao DiDeng Ai－min
China Ship Development and Design Center， Wuhan 430064， China

Based on the model test data of five double－stepped planing crafts， the multiple linear regression method was used to treat the test data and thus a resistance regression formula was obtained for the craft with different parameters of its double steps.Then， the accuracy of the regression formula was verified through the relative error analysis.Finally，the regression results were plotted in charts so as to be references for design.

double－stepped planing craft； multi－factor linear regression； resistance regression formula；relative－error analysis method

U661.3

A

1673－3185（2010）02－59－05

2009－04－16

沈小红（1980－），女，硕士研究生。研究方向：船舶与海洋结构物设计制造。E-mail：shenxiaohong304＠163.com

吴启锐（1965－），男，研究员，硕士生导师。研究方向：船舶与海洋结构物设计制造