我国教育投资与经济增长关系分析

□文/赵 妍 陈 刚 赵 婕

我国教育投资与经济增长关系分析

□文/赵 妍1陈 刚1赵 婕2

本文拟采用面板数据模型，分析我国教育投资和经济增长的关系，并给出教育投资的一些建议。

面板数据；教育投资；经济增长

一、面板数据模型

面板数据模型也称截面时序模型，其基本思想是：假定我们抽取一个数目为N的样本，对样本中的每一个体观测T年（或月），就形成一个样本为NT的新样本，这就是时间序列与截面数据结合资料，用这样的资料建立的模型称为Panel Data模型。

其中，yit是因变量，xit是K×1维解释变量向量，N为截面成员个数，T为每个截面成员的观测时期总数。参数αit表示模型的常数项，βit为对应于回归向量xit的系数向量。随机误差项uit相互独立，且满足零均值、等方差的假设。在个体成员截面上，该模型共含有N个截面成员方程，在时间截面上，该模型共含有T个时间截面方程。

模型有如下三种具体类型：

1、不变参数模型（不变截距、不变系数）：

2、变截距模型（变截距、不变系数）：

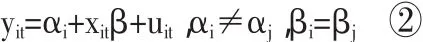
在横截面上个体影响不同，个体影响表现为模型中被忽略的反映个体差异的变量的影响，又分为固定影响和随机影响两种情况。变截距模型又分为固定影响变截距模型和随机影响变截距模型两种。

3、变参数模型（既变截距又变系数）：

如果模型形式设定不正确，估计结果将与所要模拟的经济现实偏离甚远。因此，建立面板数据模型的第一步就是检验被解释变量yit的参数αi和βi是否对所有个体截面都是一样的，既检验样本数据究竟符合上面哪种面板数据模型形式，从而避免模型设定偏差。经常使用的检验是协方差分析检验，主要检验如下两个假设：

可见，如果接受假设H2，则认为样本数据符合不变系数模型，无须进行进一步检验。如果拒绝假设H2，则需检验假设H1。如果拒绝假设H1，则认为样本数据符合变系数模型；反之，则认为样本数据符合变截距模型。

在众说纷纭的观点面前，有时候准妈妈们难免有点不知所措，不知道该听谁的。这种情况下，请信赖你的医生，听从他的建议，切忌盲目坚持己见，干扰分娩过程。

首先，对模型③回归，得到残差平方和，记为S1；

其次，对模型②回归，得到残差平方和，记为S2；

再次，对模型①回归，得到残差平方和，记为S3；

最后，识别：

（1）在假设H2下，检验统计量F2服从相应自由度下的F分布，即：

若根据上式计算得到的统计量F2的值不小于给定置信度下的相应临界值，即以（N-1）（k+1）为分子的自由度，以N（T-k-1）为分母的自由度，查F分布表，得到临界值，则拒绝假设H2，继续检验假设H1；反之，则识别为模型①。

（2）在假设H1下，检验统计量F1也服从相应自由度下的F分布，即

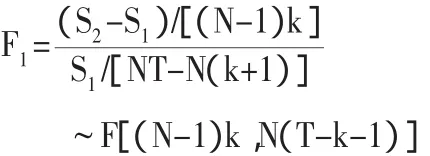
若根据上式计算得到的统计量F1的值不小于给定置信度下的相应临界值，即以（N-1）k为分子的自由度，以N（T-k-1）为分母的自由度，查F分布表，得到临界值，则拒绝假设H1，用模型③；反之，则识别为模型②。

二、实证分析

考虑数据的可得性，本文选取《中国统计年鉴》1997～2005年31个省及直辖市的年度数据，建立面板数据模型，东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东、海南等11个省（区、市），中部地区包括山西、吉林、黑龙江、安徽、江西、河南、湖北、湖南等8个省，西部地区包括重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆、广西、内蒙古等12个省（区、市）。模型中的被解释变量为各地区教育经费，记为EDU，解释变量为各地区生产总值，记为GDP，分析我国教育投资与经济增长的关系。为了消除异方差行，对两变量分别取对数。利用以上介绍的模型形式设定检验方法（N=31，k=1，T=9），先将模型设定为：

要想对两变量建模，首先要进行检验，确定建立哪种面板数据模型。

首先，假定模型为变参数模型，对模型回归得到残差平方和S1=1.023338。

其次，假定模型为变截距模型，对模型回归得到残差平方和S2=1.896122。

最后，假定模型为不变参数模型，对模型回归得到残差平方和S3=19.54528。

由于N=31，T=9，K=1，根据上述计算公式可以得到两个检验统计量：F2=65.68，F1=6.18。给定5%的显著性水平，查F分布表得到临界值：F0.05（60，217）=1.38，F0.05（30，217）=1.51。

由于F2＞1.38，所以在给定的自由度水平下拒绝原假设H2；继续检验H1，由于F1＞1.51，在给定的自由度水平下拒绝原假设F1，故模型应该是变系数模型。由于本文对31个省及直辖市的样本本身进行分析，故采用固定影响变系数模型，将模型设定为：

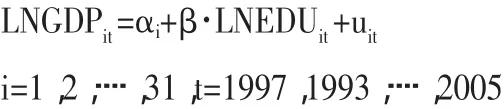
表1 教育投资与GDP的面板数据模型回归分析结果

这里假定它满足古典线形回归的所有假定，为了减少面板数据造成的异方差性，在回归估计时使用广义最小二乘法GLS方法对模型进行估计，估计结果见表1。检验结果分为两部分，第一部分是解释变量EDU对各截面成员的系数及估计结果，例如北京的系数为0.95，表示北京地区的教育投资对北京GDP的影响程度，当北京的教育投资增加1%时，将拉动GDP0.95个单位；第二部分是评价总体估计效果的统计量，由于估计方法选择的是GLS估计，所以结果给出了加权和未加权两种情况下的评价统计量。从表1中可以看出，加权后的模型R2显著提高，所以采用GLS估计要比OLS估计更合理，在显著水平0.05下模型没有显著的异方差和自相关，故模型拟合较好。（表1）

三、结论及政策建议

从模型的回归系数看，各地区的教育投资对经济增长有显著的促进作用，但全国各地区回归系数相差较大。换句话说，全国各地区的教育投资对经济增长的贡献各有所异。弹性系数最大的10个省市，其中东部地区有6个，中部地区有3个，西部地区只有1个，弹性系数最小的8个省份全部是中西部地区。总体来说，东部省份的教育投资产出弹性明显高于中西部，中西部的低弹性表明中西部经济和知识经济联系并不紧密，这是由东部和中西部地区的经济发展程度所决定的。造成这种地区贡献差距的主要原因是：

1、东部地区的制度更完善，政策更灵活，市场经济的作用更强。东部沿海地区的改革开放领先于全国，已经具备了良好的体制框架，市场化的进程也明显快于中西部地区，有利于高素质人力资本跟当地的经济更加有效地结合，使其经济作用得到充分发挥，更有效地转化为生产力，教育投资的转化效率比较高。而西部地区由于体制和市场化程度等原因，教育投资的转化效率比较低，教育投资对经济增长的拉动作用也较小。

2、人才的地域流动。教育投入的产出就是人力资本，人才就是拥有较大人力资本的受教育者。由于东西部经济发展的不平衡性以及国家放松对人才流动的限制，我国人才流动呈现出自西向东流动的局面，西部对教育和人力资本的投资成果流入到东部，为东部的经济增长做贡献。因此，西部的教育投资并没有全部用来促进当地经济的增长。而东部由于无偿获得人力资本，教育投资的作用被放大。

3、教育对于经济增长的作用在经济发展过程中表现为先弱、后强、最后稍有降低的趋势。东部经济发展水平较高，教育对经济增长的作用正处于第二阶段，中西部经济发展水平较低，教育对经济增长的作用还正处于第一阶段。故教育投入弹性高低和教育结构与当地经济发展水平结合程度密切有关。

针对我国教育投入产出弹性高低不均的这种现象提出如下建议：第一，调整教育投资结构，提高基础教育特别是中西部的基础教育投资比例；第二，为西部人才提供更优越的物质条件和更好的福利政策，鼓励人才向西部发展，为西部经济增长做贡献；第三，继续“西部大开发”，发展西部市场经济，完善西部体制建设，使人力资本更有效地拉动经济；第四，继续控制人口数量，引导人才的合理流动；第五，推进教育投资主体多元化，鼓励民办教育。

[1]罗建平，刘俊花.内蒙古自治区教育投资对经济增长的计量分析[J].内蒙古财经学院学报，2008.2.

[2]樊端成，凡兰兴.新型工业化与广西高等教育发展战略调整[J].广西社会科学，2006.12.

[3]高铁梅.计量经济分析方法与建模[M].清华大学出版社，2006.

F12

A

1.河北经贸大学经济研究所；2.中国联合通信集团公司）