巡航导弹飞行初段弹道交叉近似计算方法研究

孟 伦，赵冠光，刘晓亮，张 彤

（第二炮兵工程学院，陕西 西安 710025，）

巡航导弹是现代战争的“杀手锏”武器，也是决定战争胜负的一个主要武器因素。但如何在战前制定作战方案，进行火力分配，从而在选择发射阵地阶段避免出现弹道互扰现象的出现，变得越来越重要。

1 初段弹道交叉现象介绍

巡航导弹飞行初段，是指巡航导弹从发射阵地起飞，至导弹弹载计算机装订的航迹的第一导航点之间的飞行轨迹。巡航导弹飞行初段弹道交叉，是指在同一波次任务中，两条巡航导弹飞行初段的飞行轨迹之间的空间最短距离小于3σ，则称这两条飞行轨迹之间产生弹道交叉。

在一波次火力打击任务中，假设使用不同航迹和发射阵地来完成波次任务（如图1所示）：发射阵地1、发射阵地4上的导弹，采用航迹1对目标1进行攻击；发射阵地2、发射阵地3上的导弹，采用航迹2对目标2进行攻击；由于航迹1的第一导航点1和航迹2的第一导航点2的位置影响，发射阵地1和发射阵地2上的导弹飞行初段，出现弹道交叉1；以及发射阵地3和发射阵地4上的导弹飞行初段，出现弹道交叉2。

如果有弹道交叉现象，则可能发生弹道互扰，应避免这种现象的发生。

2 初段弹道交叉解析近似计算模型

2.1 巡航导弹飞行初段的简化模型

巡航导弹飞行初段的飞行轨迹，由出筒、爬升、下滑、平飞共4段组成。从发射阵地到转平飞点Azp阶段，所经历的时间相当短，导弹飞行的距离有限。经统计数据分析，这一阶段发生弹道交叉的概率比较低，故我们只需考虑导弹从转平飞点Azp到第一导航点Cdf之间导弹飞行初段的飞行轨迹即可。根据现有武器性能，巡航导弹由转平飞点Azp到第一导航点Cdf之间的飞行状态为平飞，中间至多有一个转弯点Bzw，则其飞行轨迹可近似看成为三维空间内的二条线段AzpBzw、BzwCdf，要确定三维空间内的一条线段，只需知道其两个端点的坐标即可。Bzw和Cdf的坐标，由航迹数据给出，Azp可由发射点坐标经过初段飞行航迹计算获得。

设Azp点的坐标为（xzp，yzp，zzp），Cdf点的坐标为（xdf，ydf，zdf），Bzw点的坐标为（xzw，yzw，zzw），则巡航导弹飞行初段的飞行轨迹为线段AzpBzw和BzwCdf，其解析表达式为

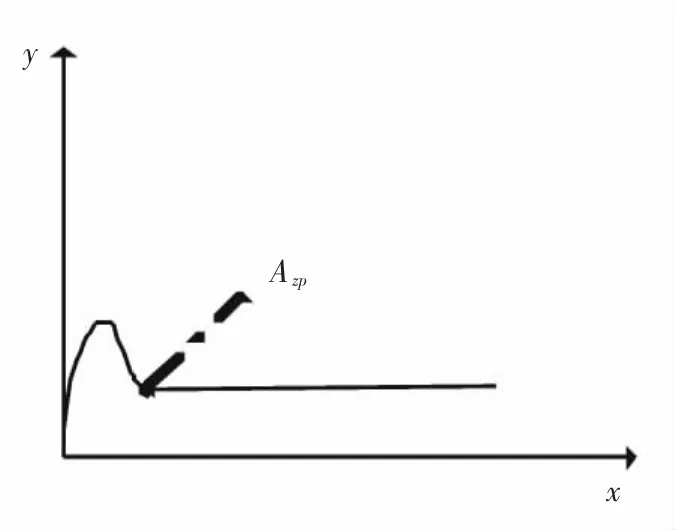
图2 巡航导弹飞行初段飞行轨迹示意图

2.2 计算弹道交叉的近似解析方法

两个导弹飞行初段出现弹道交叉，是指两个飞行初段的飞行轨迹之间的最短距离小于3σ，则求巡航导弹飞行初段弹道互扰问题，就转化为求空间两条线段最短距离的问题。

设空间中有两条线段AB和CD，设A点的坐标为（x1，y1，z1），B 点的坐标为（x2，y2，z2），C 点坐标为（x3，y3，z3），D 点坐标为（x4，y4，z4）。

设P是直线AB上的一点，P点坐标（X，Y，Z）可以表示为：

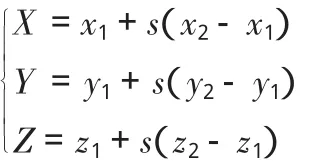
当参数0≤s≤1时，P是线段AB上的点；当参数s＜0时，P是BA延长线上的点；当参数s＞1时，P是延长线上的点。

设 Q是直线 CD上的一点，Q点坐标（U，V，W）可以表示为

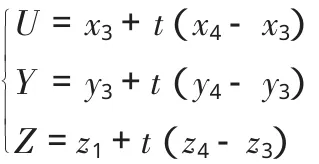
当参数0≤t≤1时，Q是线段CD上的点；当参数t＜0时，Q是DC延长线上的点；当参数t＞1时，Q是CD延长线上的点。

P、Q两点之间的距离为

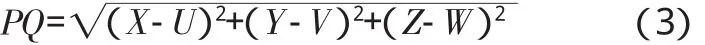
距离的平方为

要求直线AB、CD之间的最短距离，也就是要求f（s，t）的最小值。对f（s，t）分别求关于s、t的偏导数，并令偏导数为0。

展开整理后，得到下列方程组

如果从这个方程组求出的参数s、t的值满足0≤s≤1、0≤t≤1，说明P点落在线段AB上，Q点落在线段CD上，这时PQ的长度

就是线段AB与CD的最短距离。

如果从方程组求出的参数s、t的值不满足0≤s≤1、0≤t≤1，说明不可能在线段AB内部找出一点P，在线段CD内部找出一点Q，使得PQ的长度就是线段AB与CD的最短距离。

这时，可以分别求A点到线段CD的最短距离、B点到线段CD的最短距离、C点到线段AB的最短距离、D点到线段AB的最短距离。然后比较这4个距离的大小，其中最小的一个就是线段AB与CD的最短距离。

3 巡航导弹旅发射阵地弹道交叉计算流程

巡航导弹旅发射阵地弹道交叉计算流程如图3所示。

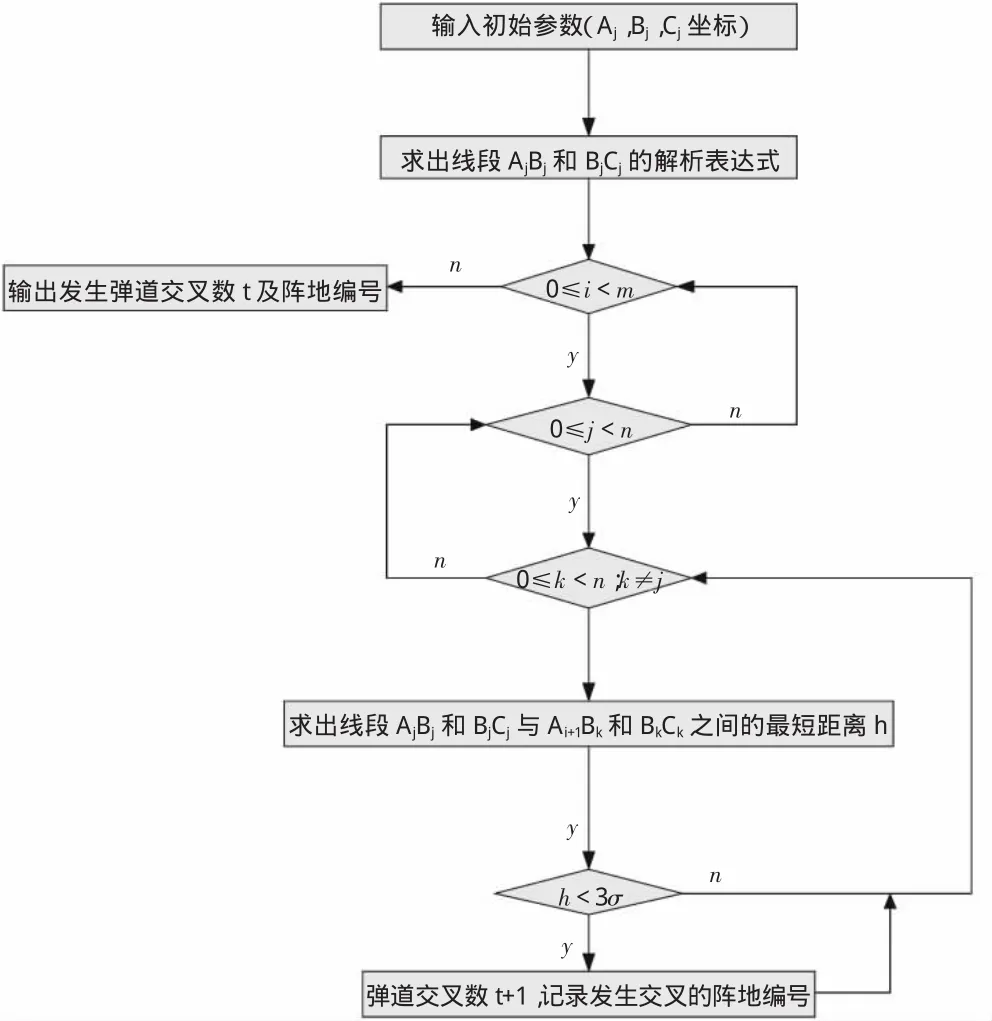
图3 弹道交叉计算流程

4 结束语

本文针对巡航导弹飞行初段的特点，建立了巡航导弹飞行初段简化模型，运用近似解析计算的方法，求解巡航导弹飞行初段弹道交叉问题，方法简单，易于计算机实现，为作战中快速科学、合理地选择发射阵地、制定火力计划提供有效支持，具有一定的应用价值。

[1]同济大学数学系.高等数学（第6版）[M].北京：高等教育出版社，2007.

[2]李小波.巡航导弹发射阵地选择的多目标决策[D].第二炮兵工程学院，2003.