基于AHP的专业课课堂教学评价研究

高淑雅， 郭宏伟， 周小华， 龚煜轩

(陕西科技大学材料科学与工程学院， 陕西 西安 710021)

0 引言

学校的根本任务是育人，育人的载体在专业.如何对专业课课堂教学质量进行评价是一个综合的、带有一定模糊性的问题，涉及到多因素、多层次，而且各因素在教学过程中既密切相关，又权重不同.如何构建评价的指标体系，尽可能克服主观因素，提高评价结论的可信度，是值得各高校认真思考的问题.

以往对课堂教学的评价是从以“教”为中心，把教学看成知识传授的过程，并制定一系列的指标评价知识传授的水平.新课程提倡的教学观认为，课堂教学是一个互动的过程，影响这一过程的主要因素包括学生、教师、教学内容以及教学环境.学生是学习的主体，是知识的主动建构者；教师是学生学习的组织者、促进者、引导者，是学生的朋友及长者.教学内容是充满活力的知识载体；教学环境是激发和促进互动的背景元素[1].科学地评价课堂教学质量，是评价教学水平、总结教学经验、促进教学改革的必要措施.然而，课堂教学质量是由多种因素构成的质量体系，且每一因素给予评课人的感受在许多情况下是一种缺乏明确边界的信息.那么，怎样评价工科类高校专业课课堂教学的质量？本文结合所属专业认为，评价工科类高校专业课课堂教学质量，不仅要掌握简明扼要的评价指标体系和评课人客观地摄取隶属于各评价指标的质量信息，而且需要借助于合理的数学方法将这些信息进行加工并表达出来，这样得到的评价结论才具有较强的科学性、合理性及可信度.为了使评价结果更加科学合理、更具有广泛的民主性，排除一切人为因素对评价结果的影响，本文采用层次分析法，通过建立数学模型，构建了专业课课堂教学质量评价指标体系，从而使评价定量化.

1 层次分析法

层次分析法(analytic hierarchy process)简称AHP，在20世纪70年代中期由美国运筹学家托马斯.塞蒂(T. L. Saaty)正式提出.它是一种定性和定量相结合的、系统化、层次化的分析方法.由于在处理复杂的决策问题上的实用性和有效性，使其很快在世界范围得到了重视.它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域[2,3].层次分析法的4个基本步骤如下：

(1)建立层次结构模型：在深入分析实际问题的基础上，将有关的各个因素按照不同属性自上而下地分解成若干层次，同一层的诸因素从属于上一层的因素或对上层因素有影响，同时又支配下一层的因素或受到下层因素的作用.最上层为目标层，通常只有1个因素，最下层通常为方案或对象层，中间可以有一个或几个层次，通常为准则或指标层，当准则过多时(譬如多于9个)应进一步分解出子准则层.图1是本文所建立的专业课课堂教学评价递阶层次结构模型，方案层C具体内容如表3所示.

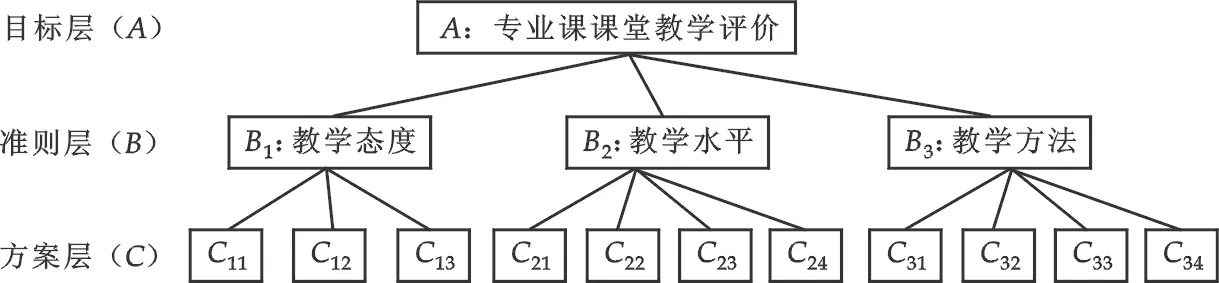
图1 专业课课堂教学评价递阶层次结构模型

(2)构造成对比较阵：从层次结构模型的第2层开始，对于从属于(或影响)上一层每个因素的同一层诸因素，用成对比较法和1～9比较标度构造成对比较阵，直到最下层.表1为萨蒂比较标度及解释.

表1 1～9比较标度及解释

(3)计算权向量及一致性检验：对于每一个成对比较阵计算最大特征根λmax及对应特征向量w0，利用一致性指标、随机一致性指标和一致性比率做一致性检验.若检验通过，特征向量(归一化后)即为权向量；若不通过，需重新构造成对比较阵.其检验步骤为：

①计算一致性指标CI.可以通过下式计算：

(1)

式中n为矩阵阶数.CI是衡量比较判断矩阵不一致程度的标准.

②查找平均随机一致性指标RI.RI的取值如表2所示.

表2 平均随机一致性指标

③计算随机一致性比率CR.可以通过下式计算：

(2)

当CR<0.1时，认为比较判断矩阵具有满意的一致性，可将其特征向量作为权重向量.否则，需对比较判断矩阵作重新调整，直到达到满意的一致性为止.

(4)计算组合权向量并做组合一致性检验：计算最下层对目标的组合权向量，并根据公式做组合一致性检验，若检验通过，则可按照组合权向量表示的结果进行决策，否则需要重新考虑模型或重新构造那些一致性比率较大的成对比较阵.总排序权重向量各分量的计算公式为：

(3)

总排序随机一致性指标计算公式为：

(4)

当CR<0.1时，认为层次总排序结果具有满意的一致性.否则，应重新调整比较判断矩阵.

2 层次分析法在专业课课堂教学评价中的应用

2.1 构建专业课课堂质量评价体系

在建立大学专业课课堂教学评价指标体系时，应从学生的角度出发，以学生为中心，突出学生在评价中的中心地位.根据大学专业课课堂教学的特点，概括为以下几个方面：(1)教学态度.教学态度反映教师对教学工作的素质特征，如敬业精神、工作态度等.课堂教学强调教师和学生的双向交流，教师为课堂教学的主导，特别要和教学的主体——学生进行交流.(2)教学水平.教学水平反映了教师教学水平的本质特征，如业务水平、知识面的宽泛程度及对所授课程的相关领域是否熟悉、讲解的逻辑性与条理性是否清晰，能否被学生理解和接受等.(3)教学方法.教学方法指标按目标模式设置，不涉及具体教学方法和教学风格的项目，以克服模式化教学为向导，鼓励教师有自己的创新和教学改革，认可不同的教学风格和教师的个体差异[4-6].本文结合专业所属的轻工业特征，制定了专业课课堂教学评价体系，如表3所示，建立的递阶层次结构模型如图1所示.

表3 专业课课堂教学评价体系

2.2 构造比较判断矩阵

根据比较判断矩阵的构造方法，将专业课课堂教学质量评价体系中的各具体方案采用萨蒂的9标度法制成调查问卷，并将问卷提交学院及学校教务管理部门的专家与老师审核.邀请本校无机非金属材料工程专业3个毕业班的90余名学生对指标体系进行填写打分，然后将收集到的数据进行整理、归纳，得到各层次的若干两两比较判断矩阵，如表4～7所示.

2.3 层次单排序及一致性检验

利用Matlab7.0求出各比较判断矩阵的最大特征值λmax及对应特征向量(权重向量)w0，利用式(1)和(2)分别计算一致性指标CI和随机一致性比率CR，并采用一致性比率做一致性检验.当CR<0.1时，认为比较判断矩阵具有满意的一致性，可将其特征向量作为权重向量.否则，需对比较判断矩阵作重新调整，直到达到满意的一致性为止.计算结果如表4～7所示.

表4 矩阵A-Bi指标权重及一致性检验

表5 矩阵B1-C1j指标权重及一致性检验

表6 矩阵B2-C2j指标权重及一致性检验

表7 矩阵B3-C3j指标权重及一致性检验

2.4 层次总排序及整体一致性检验

由层次单排序，计算出准则层(B)相对于目标层(A)的排序向量以及指标层相对于准则层的权重，其中指标层相对于目标层的层次总排序可通过公式(3)、(4)计算出来.根据公式做组合一致性检验，当CR<0.1时，认为层次总排序结果具有满意的一致性，否则应重新调整比较判断矩阵，结果如表8所示.由表8可以看出，通过层次总排序一致性检验，所有判断具有整体的一致性.

表8 层次总排序结果

3 结果分析

对学生来说，不管是找工作，还是考研，专业课都是非常重要的.怎样才能讲好专业课及如何对专业课课堂教学质量进行评价是一个综合的、带有一定模糊性的问题.本文运用层次分析法计算出了轻工类专业课课堂教学评价指标体系中各指标的权重，以此为例介绍了一种解决问题的方法.

由表8中的层次总排序结果可以看出，学生对一位专业课老师的评判首要看重的是这位老师的教学水平，它相对于总目标的权重为0.558，其次是教学方法和教学态度，相对于总目标的权重分别为0.320和0.122，这一结果比较符合轻工类专业的客观实际.因为专业课的专业性、特殊性较强，如果教师没有一定的理论知识和实践经验，讲课过程中就不能理论联系实际，内容就没有深度、广度及先进性，课堂教学过程就比较枯燥.在当前就业、考研的重重压力下，学生的学习积极性将受到严重影响，进而达不到应有的教学效果.

从学生的调查问卷来看，对于专业课教学评价的前5位分别是：理论联系实际，内容先进；参观实习，合理使用多媒体；重点突出，深度和广度适合；发表科研及教学论文和布置作业灵活，这些要求正好与国家新课程的教学理念相吻合，充分体现了学生是学习的主体和主动的建构者，教师是学习的组织者、引导者、促进者和学生的朋友及长辈，教学内容是知识的载体，教学环境是促进互动的情境.

[1] 许数柏.层次分析原理[M]. 天津：天津大学出版社, 1988.

[2] 梁惠燕,高凌飚.课堂教学评价的反思和框架重构[J].教育科学研究,2006,(6):20-23.

[3] 陈 刚,张 伟,李海霞.高校网络课程实施质量的评价标准[J].清华大学教育研究,2003,(5):98-102.

[4] 陈 赟,唐仁春，张风明.AHP法在高教学生质量评价中的应用[J].中国高教研究,2005,(7):9-11.

[5] 杨 萍.AHP法在评价教师课堂教学中的应用[J].数学的实践与认识,2004,(2):32-34.