基于FAHP的第三方物流供应商选择的研究

王 蕊

(新疆轻工职业技术学院计算机系， 新疆 乌鲁木齐 830021)

0 引 言

在如何选择第三方物流(3PL)供应商的问题上国际国内提出了一些较为客观的方法，也进行了一定的定性分析.最初人们采用线性权重模型，1973年美国学者T.L.Saaty教授提出了层次分析法(AHP)[1]， 1996年Filip Roodhooft和JozefJoings提出了作业成本法(Activity Based Costing, ABC )[2],1998年Ghodsypour和Brien采取层次分析法(AHP)和线性规划(LP)相结合的方法对供应商选择的决策问题进行了研究[3]，2000年Isao Shiromaru等人采用模糊理论研究了供应商选择中的模糊目标问题[4].在国内，1999年蔡鹤皋等采用层次分析法建立了选择供应商的数学模型，并在Matlab环境下开发了一个供应商选择系统[5].2004年，王旭坪、陈傲同时综合了DEA和AHP两种常见评价方法的优点，提出了基于AHP/ DEA的供应商选择方法，为供应商的评价和优化提供了依据[6].

1 第三方物流供应商评价选择方法及基于对数三角模糊数的层次分析法

本文参照一些关于供应链中供应商选择的方法来进行评价选择.近几年出现的新方法有：多阶段优化算法、模糊决策方法、遗传算法、数据包络分析(DEA)、多维标度法、成本法、神经网络法等等.层次分析法的核心是利用1～9间的整数及其倒数作为标度构造判断矩阵，这种判断往往没有考虑人的判断的模糊性.如果i，j两个因素的权重之比不易确定，只知道其变化范围在1和u之间，最大可能值为m，则这就是模糊判断.基于这种认识，层次分析法在模糊环境下的扩展是必要的，这一扩展称为模糊层次分析法(Fuzzy-AHP)[7，8]，是模糊综合评判和层次分析法相结合而产生的一种综合评价方法.1983年荷兰学者Van Laarhoven提出了用三角模糊数进行比较判断的方法，并运用三角模糊数的运算和对数最小二乘法求得元素的排序，即在模糊环境下使用的层次分析法.

1.1 基于对数三角模糊数的层次分析法[9-11]

计算单一准则下元素的相对权重时可以采用对数“最小二乘法”来求解权重向量，即针对式(1)求Z的最小值，从而求出一个向量W= (w1,w2,…,wn)T作为W的近似解：

(1)

在3PL供应商选择问题中，由于评选委员会是由多位专家组成的，判断矩阵A中的元素aij可能有多个值(表示不同专家的意见)，因而，式(1)可以扩展为：

(2)

在式(2)中，aijt(t=1,2,…,θ)表示元素ui和uj之间有θ个比较，θ=0表示ui和uj之间没有比较.在一般情况下，θ为一常数，即专家的数目.

为求Z的最小值，将式(2)两边对wk,k=1,2,…,n取偏导数，并使其等于0，得到

(3)

从而有

(4)

此时，用三角模糊数来代替式(4)中的元素，令wk=(lk,mk,uk),akjt=(rkjt,skjt,tkjt)，则式(4)可转化为

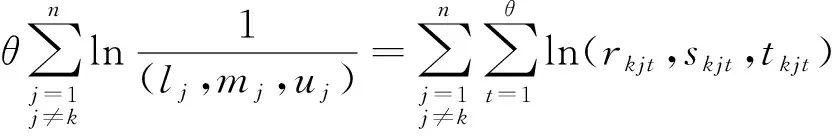
(5)

由三角模糊数的加、乘、逆、对数和幂等运算规则和比较规则得

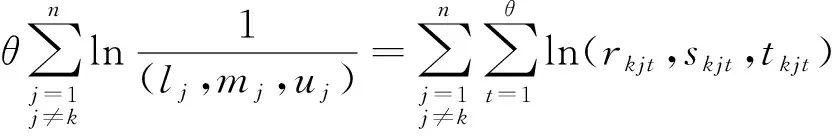
(6)

对于k=1,2,…,n有

(7)

(8)

(9)

由于akjt=(rkjt,skjt,tkjt)为已知值，从而根据式(7)、(8)、(9)可求出wk=(lk,mk,uk).最后，将得到的向量wk归一化，可得

(10)

综上所述，采用基于对数三角模糊数的层次分析法，客观对象的选择和评价过程可以归纳成以下几个步骤：

(1)由各专家组成评审小组.

(2)确定每层的三角模糊判断矩阵R，计算出反映各准则相对重要性的权重值.

(3)由上至下计算出各层准则相对于目标层的合成权重，直至最后一子准则层(假设最后一子准则层中各子准则Ai相对于目标层的合成权重向量为W).

(4)根据已有资料数据计算出各个方案在最后一子准则层下的相对权重矢量Wsn,其中s为递阶结构的层数，n为候选方案个数.

(5)从Wsn⊙W计算出每个方案相对于目标层的总权值，同时还可以根据Wsn指出各个方案的强项以及需要改进的方面.

1.2 实例分析

下面，随意抽取3家3PL供应商企业A，B，C，举例说明采用对数三角模糊数的层次分析法对它们进行排序的过程，并在最后做出综合评价.

(1)求物流能力评价、企业服务质量、合作关系评价、信息服务能力和发展潜力评价的权重Wi.设有3位专家001，002，003(实际上，参加评审的专家数量可以没有限制)针对这5项准则的权重填写了三角模糊数判断矩阵.根据判断矩阵，计算出各准则的权值，将物流能力评价、企业服务质量等5个准则的权重分别定义为W1，W2，W3，W4，W5.

(2)求准则下各子准则的权重Wij.通过专家对所属子准则的比较得到一个三角模糊数判断矩阵，根据判断矩阵计算出各子准则的权值.将物流吞吐能力、物流技术、物流设备、公司经营业绩4个子准则的权重分别定义为W11，W12，W13，W14.用同样的方法求出其他准则下各子准则的权重值Wij，然后利用公式Wi⊙Wij(i=1,2,3,4；j=1,2,3,4)求出各子准则相对于目标层的组合权重.

(3)求出各候选3PL供应商企业在各子准则下的权重Wst.大部分子准则都是定量指标，可以采用精确的统计数据.对于有些子准则，无法用精确的数据来表示，但此时可以通过设定评价等级将该准则指标拟量化.此外，对于有些定性子准则，虽然也可将其拟量化，但这样势必会使得模型和计算复杂度大大增加.可以采用模糊层次分析法，即通过构建两两比较的判断矩阵来确定各3PL供应商在这些子准则下的权重值.同时，3PL供应商相对于各准则的权值是一个三角模糊数，其对应的关系函数如图1所示，可用3PL供应商在物流能力评价准则下的三角模糊数权重表示.

图1 3PL供应商在物流能力评价准则下的三角模糊数权重表示 图2 各供应商总权重的三角模糊数表示

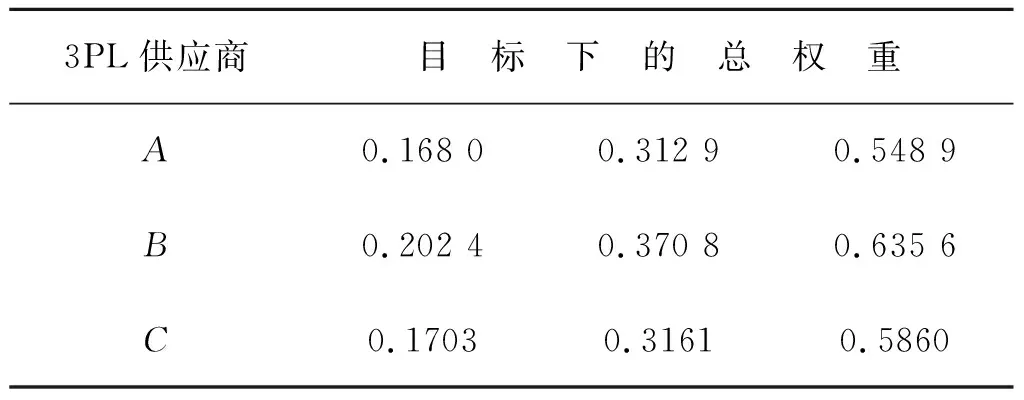
表1 3PL供应商的总权值

最后，求出各3PL供应商在目标层下的总组合权重，如表1所示.图2是其三角模糊数的对应关系函数.

从以上过程得到如下结论：

(1)根据表1或图2，结合公式可以得出：企业B最佳，A和C差别不大，C略好一些.

(2)根据图1及其他物流能力评价准则下的三角模糊数权重表示，可得各3PL供应商在各准则下的排序情况，这样就可以在这5个指标下了解到各企业的强项和需要改进的地方.

(3)各企业在各个子准则下的情况也可以一目了然，此处不再进一步做列表和分析工作.

2 结束语

采用模糊层次分析法(Fuzzy-AHP)克服了层次分析法中所构造出的判断矩阵没有考虑到人的判断的模糊性的问题.当某两个因素之间的权重之比不易确定时，只要知道其变化范围在某一区间和在此区间上最有可能的值，即引入三角模糊数进行模糊判断.然后，在该基础上开展后续的层次分析.Van Laarhoven提出的基于对数模糊三角数的层次分析法易于理解、公平性高，更重要的是使得决策的过程更加接近人的思维过程，因此本文按照这一理论较好的实现了第四方物流中3PL供应商的选择问题.

参考文献

[1]T.L.Saaty，J.M.Alexander. Thinking With Models: Mathematical Models in the Physical Biological and Social Sciences[M].London:Chapter8.Pergamon Press，1981.

[2]Filip.Roodhooft, Jozef.Konings.Vendor selection and evaluation. an activity based costing approach[J].European Journal of Operation Research， 1996,(1)：96.

[3]S.H Ghodsypour， C.O′Brien. A decision support system or supplier selection using an integrated analytic hi erarchy process and linear programming[J].International journal of Production Economics,1998,(2):56.

[4]Isao Shiromaru. A fuzzy ssatisficing method for electric power plant coal purchase using genetic algorithms[J].Operational Research,2000,(3):126.

[5]蔡鹤皋,马永军，张福顺.网络联盟企业中的供应商选择方法[J].小型微型计算机,1999,(11):15-18.

[6]王旭坪,陈 傲.基于电子商务的供应商评价与优化[J].管理科学. 2004,(4):69-71.

[7]吴国通,高雷阜.层次分析法在选择第三方物流供应商中的应用[J].科学技术与工程，2005,4(2)：46-48.

[8]Iai S．A preference-based interpretation of AHP[J].Omega,1995,(23)：453-462.

[9]樊治平，姜艳萍.一种三角模糊数互补判断矩阵的排序方法[J].系统工程与电子技术，2007,7(5)：67-69.

[10]刘礼金,范如国 .基于三角模糊数比较大小原理的模糊层次分析法在供应商合作伙伴选择中的应用[J].物流科技，2006,3(3)：33-35.

[11]雷国雨,肖光灿.三角模糊数方程的简便求解[J].西南科技大学学报(自然科学版)，2008,4(2)：148-150.