稀疏效应下第Ⅳ类功能反应系统的定性分析
2010-02-23窦霁虹
曹 明, 窦霁虹, 贾 娟
(西北大学数学系, 陕西 西安 710127)
0 引 言
食饵-捕食系统在生物学的研究中具有十分重要的作用和意义,不少学者对反映两种群在相互作用下变换规律的Lotka-Volterra数学模型:
(1)


(2)

对系统(2),先令dt=(β+x2)dt,且仍记τ为t,则式(2)化为
(3)
(4)


1 系统的奇点分析
(1)当a42<4a3时,系统(4)在第一象限内无正平衡点,因此无环.


定理1.1
(1)奇点O为系统(4)的鞍结点,且左边为结状,右边为鞍状.
(2)若a42>4a3且x4 (3)若a42=4a3时奇点E2为系统(4)的鞍结点,且左边的结状,右边为鞍状. (4)若a42>4a3时奇点E3为系统(4)的鞍点. 证明:系统(4)的Jacobian矩阵为: 令p0=5a2a3x44-4a1a2x43+3a2x42-3a3x42-2a1x4-1. (1)显然奇点O为系统的高阶奇点.做时间变换t=-τ,仍记τ为t,则系统(4)变换为: (5) 由文献[5]中定理4.10知:Φ(x,y)=-x2-a1x3-a3x4+a2x4-a1a3x5+a2a3x6+xy,m=2,g=-1<0,所以O为鞍结点,且左边为结状,右边为鞍状. (2)将奇点E1代入J(x,y),当a42>4a3时,得: det(J(E1))=(2A+a1A2+2a3A3+a1a3A4)(A-x3)(A-x4) 所以,当x4 (3)类似于(1)的证明. (5)将奇点E4代入J(x,y),当a42>4a3时,得: 所以,当p0>0时,E4为稳定的焦点或结点;p0=0时,E4为中心型奇点;p0<0时,E4为不稳定的焦点或结点. 引理2.1[2]系统(4)的一切解在R内正向有界. 此引理的生态意义表明当两种群的初始密度均非零时,两种群的密度不可能无限增大,即它们之间相互制约,而且被控制在一定的范围内. 证明:由引理2.1知,系统(4)在R内出发的一切解均是正向有界的,即所有正半轨线均是有界的.而系统(4)的ω极限集只能是平衡点、闭轨线以及奇异闭轨线. 定理2.1 表明了食饵在稀疏条件下没有足够的食物提供给捕食种群时,将会导致捕食者种群灭绝,而食饵种群受自身的密度制约将会稳定在A这个水平上. 定理3.1 若x4 证明:取Dulac函数B(x,y)=x-3y-1,B(x,y)在R内一阶连续可微,则 定理4.1 若x4 证明:首先极限环的存在性由引理2.1知系统(4)的一切解在R内正向有界,且在定理的条件下知E4(x4,y4)是不稳定的焦点或结点,则由Bendixson环域定理[5]知,系统(4)在E4(x4,y4)外围至少存在一个稳定的极限环. 下证极限环的唯一性. (6) 在此变换下,则正平衡点E4(x4,y4)变为uv平面的原点(0,0). 以下我们在G={(u,v)|x4 (2)φ(u)连续且在G内部任何区间上满足Lipschitz条件,当u≠0, (3)F′(u)=f(u),令ω=u+x4,则 本文讨论了食饵种群密度制约为非线性且功能反应函数为Holling-Ⅳ的捕食系统,将文献[4]的食饵密度制约函数从二次推广到了四次,文献[4]中利用变换作系统的带域,通过调整参数域来研究系统的定型性态,而本文是通过微分方程定性理论对系统平衡点进行定性分析,并运用Dulac函数法得到了系统无极限环的充分条件,利用Bendixson环域定理和张芷芬唯一性定理证明了系统存在唯一稳定的极限环. 参考文献 [1] Kuno E.Mathematical models for predator-prey interaction[J].Advance in Ecological Research,1987,16(2):252-262. [2] 岳宗敏.一类稀疏效应下功能反应的食饵-捕食系统极限环的存在性[J].陕西科技大学学报,2007,25(3):134-136. [3] 徐鹏春,董晓梅,赵振海.稀疏效应下第Ⅲ类功能性反应系统的极限环存在性和唯一性[J].大连工业大学学报,2009,28(3):213-215. [4] 王继华,曾宪武.一类具有简化HollingⅣ类功能反应的捕食-食饵模型的定性分析[J].数学杂志,2004,24(6):701-705. [5] 马知恩,周义仓.微分方程的定性分析和稳定性方法[M].北京:科学出版社,2001. [6] 张芷芬,丁同仁.微分方程定性理论[M].北京:科学出版社,1985.
tr(J(E1))=-[2A+a1A2+2a3A3+a1a3A4+(A-x3)(A-x4)]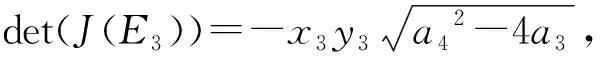
2 系统的全局稳定性


3 极限环的不存在性

4 极限环的存在唯一性
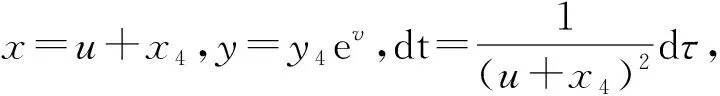
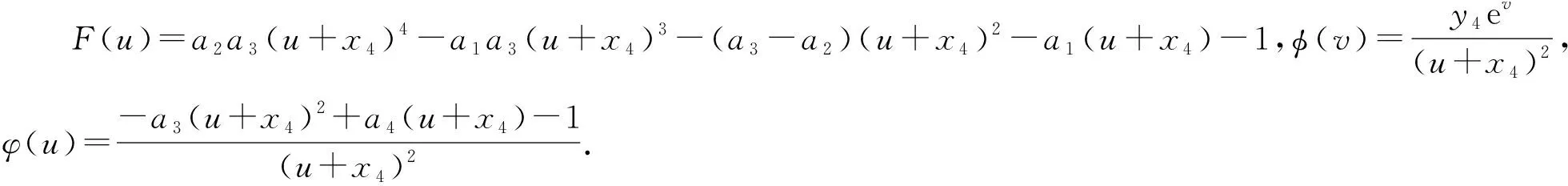



5 结束语
