改进交通流元胞机模型及其安全距离参数分析

叶丽萍, 翁小雄, 张文峰

(1.仲恺农业工程学院机电工程学院， 广东 广州 510225； 2.华南理工大学土木与交通学院， 广东 广州 510640)

0 引言

创造环境友好的交通运输是第16届智能交通系统(ITS)世界大会的主题，也是当今交通发展的主题.先进的ITS是解决交通拥塞的有效手段，然而在国内其实际的应用无法取得预期的效果.交通拥塞现象日渐严重，人民生活质量下降，经济损失和环境污染随之增长.交通系统是兼具复杂性、离散性和随机性的非线性系统，尤其是城市交通流.如何探求城市交通流复杂的内在机理，从而提出行之有效的管控措施，充分发挥交通管理系统的有效性，是ITS的热点和难点.

元胞机是一时间和空间都离散的动力系统，散布在规则网格中的每一元胞均取有限的离散状态，遵循同样的作用规则，并依据确定的局部规则作同步更新[1].1992年，Nagel和Schreckenberg提出了著名的NaSch模型[5]，首次把基于个体行为学习的元胞机模型应用于交通流仿真；1996年，Benjamin等引入慢启动步理论，对NaSch模型的更新规则进行了修正[6]；2005年，M.E. La′rraga也改进了NaSch元胞机模型[7]，模型更切合车辆动力学原理.

本文提出的改进城市交通流元胞机模型是上述理论的延伸.在该改进模型中，元胞更新规则综合考虑了车辆的慢启动和随机的速度变化效应，同时考虑到驾驶员技术、胆略及道路服务水平的差异，在减速规则引入了一个安全距离参数.

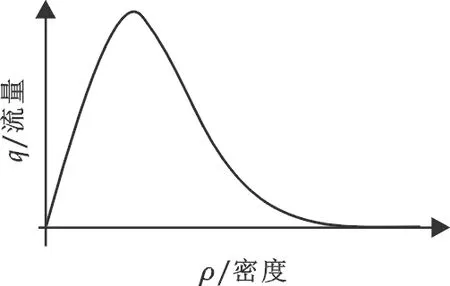
图1 Greenshields流密关系图

1 交通流相关理论

流量q、行车速度v和车流密度ρ是表征交通流特性的3个基本参数.3个参数两两之间的关系曲线是交通流的基本特性，如流量-密度关系(图1所示是Greenshields模型的流密关系)，从中可挖掘交通流的内在特征.

另一方面，由于密度数据不易采集，常用时间占有率o来代替.若车身长度标准化为定值时，占有率o与密度ρ有着如式(1)所示的线性关系，其中ρjam为堵塞密度，即道路发生致密堵塞时的车辆密度[9]：

ρ=o×ρjam

(1)

因此，占有率o与流量q、速度v有着近似于密度ρ与它们的关系.

2 改进的元胞机模型

2.1 改进元胞机模型

CA 模型摒除了一些复杂因素，假定有N辆车在环形的单车道上按同一方向行驶.随着时间的推进，车辆的状态由其当前的状态及其前面车辆的位置和速度决定：停止还是前进，又是以怎样的速度前进.

为使整条车道实现空间格子化，把整条车道假定为一排大小一样且紧紧排列的元胞空间，把车道划分成L个元胞格子.一般城市道路的阻塞密度ρ=133 vel/km，对应的车头间距为阻塞密度的倒数——7.5 m.现设每个元胞格子Δx=2.5 m，则车道上的每辆车应占据3个元胞格子，即车辆占据的3个格子状态应同时更新.一般城市道路的限速为80 km/h (22 m/s ), 车辆极限加速度为8 m/s2，现取vmax=10(对应于25 m/s)，amax=3(对应于7.5 m/s2)，则每个空间格子的状态有12种:格子空闲或该格子车辆以v=0,1,2,…,10的速度向前行驶，车辆加速度有7种状态：a=-3,-2,…，3.时间的更新步长取驾驶员的反应时间——1 s.模型中，位移、速度、时间均为整数.下一时刻空间格子的状态更新和它自身及前面相邻的格子状态有关，更新规则如下.

S1: 加速

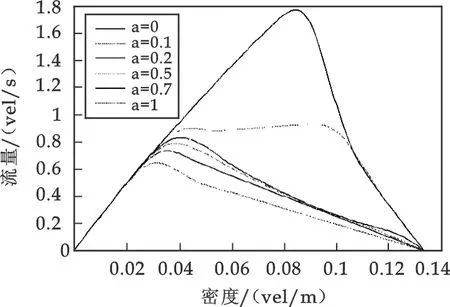
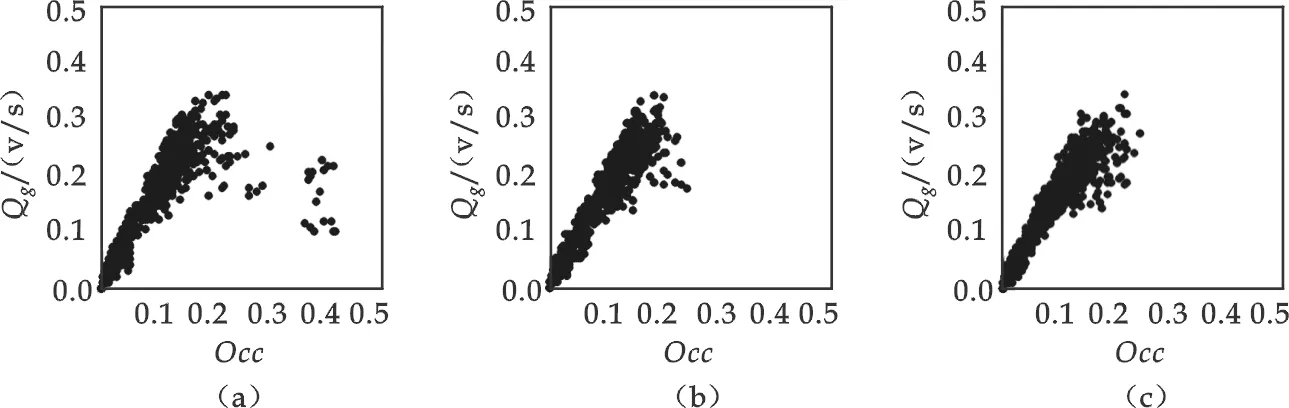
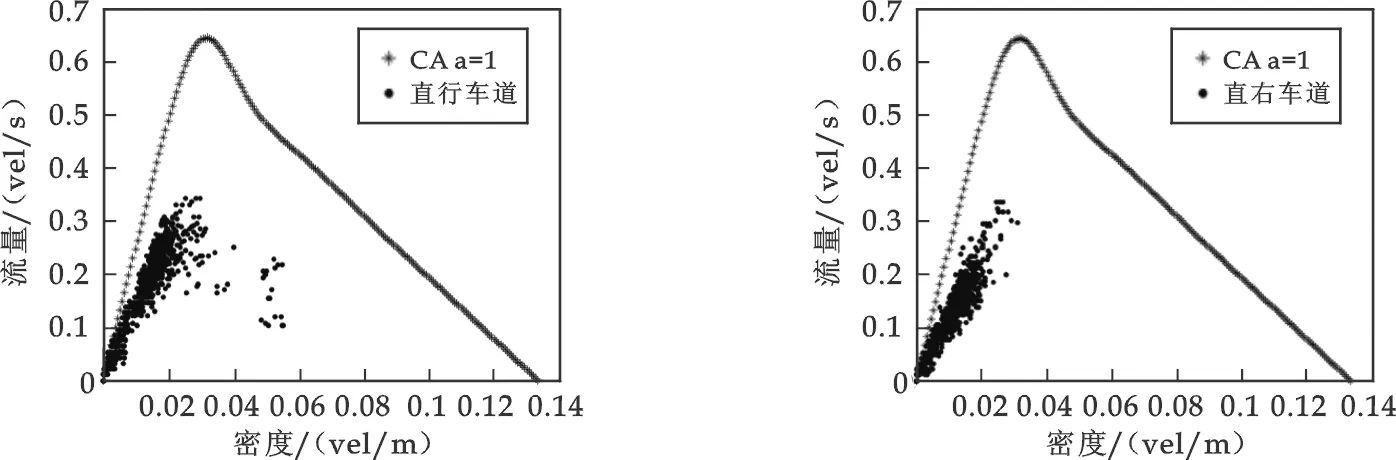
if(0

vi(t+1) = min(vi(t) + 1,vmax)

S2: 随机

if (tst,i>tsand rand()

vi(t+ 1) = max(0,vi(t)-1)

else if (tg<=tsaand rand()

vi(t+ 1) = max(0,vi(t) -1)

else if (rand()

vi(t+ 1) = max(0,vi(t) -1)

S3: 减速

If rounddi+(1-α)·vi+1(t+1)

vi(t+1)=minvi(t),round(di+(1-α)·vi+1(t+1))，α∈[0,1]

S4: 车辆静止时间tst,i的确定

if (vi(t+ 1) = 0)tst=tst, i+ 1

if (vi(t+ 1) > 0)tst, i= 0;

S5: 车辆移动

xi(t+1)=xi(t)+vi(t+1)

其中，vi(t),xi(t) 表示车辆i在t时刻的速度和位置，vi+1(t),xi+1(t)表示前车的速度和位置.di=xi+1-xi-3 表示车辆i与前车的间隔，tg为对应的车辆时间间隔，tsa为安全时间间隔，tst, i为车辆i静止时间，ts为慢启动参数，rand() 为(0，1)的随机数，α为安全距离参数，α越趋近于0，表示驾驶员的技术越好，或越果敢，又或者道路自动化性能越好.最后，随机参量设置如下pa=0.65，pb=0.25，pc=0.1.

由CA模型规则可知，车辆对其规则选择的依序是：加速规则——随机规则——减速规则.车辆随其速度更新而不断前进，那就是前进规则.

2.2 加速规则

这是假定所有司机都渴望以最大速度行驶.驾驶员在驾驶车辆过程中，首先通过自己的感官从外界环境接受信息产生知觉.在知觉的基础上，形成所谓“深度知觉”，如目测距离、估计车速和时间等.最后，驾驶员根据这种“深度知觉”形成判断，从而决定加速或是减速.而驾驶员一般都具有这样的“贪婪”特性：在条件允许的情况下，希望能以最大的速度通行.另一方面，这也是提高燃油经济性、减少交通空气污染与噪声污染的一个要求.

2.3 随机规则

体现了一些不可预见的交通事故、施工等因素对司机驾驶的影响，这些随机因素促使司机制动减速，甚至会引起交通阻塞.这个随机因素反映了驾驶员运动行为的不确定性，这种不确定性表现在以下几个方面：

(1)在最大速度附近波动.在自由流状态下，由于驾驶员精神松懈、注意力分散和个人驾驶快慢喜好不同，车辆并不总是以最大速度运动.(2)加速延迟.前车开始运动后，后车要有一定的反应时间才开始运动.(3)过度制动.当突遇前车减速时，有些驾驶员为安全起见将加大减速力度.(4)跟驰波动.在实际驾驶中，车辆不可能总是与前车保持固定的间距，其速度也随前车的变化而变化[5].

驾驶员的离散交通特性还包括除感觉-反应时间之外的动作时间及对交通信号、标志标线的反应等，因此随机规则的定义是必要的，在模型中引入随机因素使得该模型成为随机离散模型.

2.4 减速规则

减速规则是为了避免发生车辆碰撞而制定.在道路上行驶的车辆必须保持一个最小安全距离，判断条件是rounddi+(1-α)·vi+1(t-1)

2.5 前进规则

体现在车辆速度更新过程中，车辆也不断行进，驶离当前格点，前进到前面格点，xi(t+1)=xi(t)+vi·(t+1).

本文的CA模型把随机规则放在步骤(2)，减速规则放在步骤(3)，这是对NaSch模型的一个大修正.在NaSch模型中，随机规则是应用在减速规则之后，而本文的模型中随机规则在先，减速规则在后.此修正的主要原因是：当减速度值有限时，步骤(3)必须多次重复减速规则的过程以获得调和的速度值.此外，如果随机规则在减速规则后面作用时，额外的减速将会引起速度的矛盾.在改进的模型里，模型中设计随机规则主要是因为司机的不稳定行为.然而，必须注意到，如果步骤(2)要求减速，不能避免步骤(3)为了减速而要求额外的刹车制动，此时会出现模型的过度制动.

3 交通流CA模型仿真

为简化问题，将1～N辆车随机地分布在由L=3×103个紧密相连的元胞格子组成的环形单车道上，N=103，每辆车将占据3个元胞格子.仿真时间为6×103s，即共仿真6×103个时间步.车辆的初始速度为v=0～10，交通流密度ρ=N/L.由于采用周期性边界，对于行驶在车道上的头车，当其位移xlead>L时，该车就从车道前端驶出，并从车道尾部驶入车道，成为车道上的尾车，其位移xlast=xlead-L，速度vlast=vlead.

图2 α不同取值时的流密图

根据实际交通流运行机理产生的模型更新规则可再现实际的交通流现象.通过模型仿真，得到每个时间步通过车道上某断面的车流量及车道的地点平均车速.在仿真的初始时段，车道上的车辆状态(位置、速度、加速度)跟随模型规则更新的随机性较强，得到标准车辆状态的值(位置、速度等)较不稳定，故模型将仿真时段分为前后两部分，前面3×103s表示交通流稳定状态的过渡时间，后面3×103s得到的仿真结果用于平均车流量及速度的计算.由仿真得到的流量q、速度v及密度ρ可绘制得到ρ-q、ρ-v、q-v等关系曲线图.如图2所示为安全距离参数α为不同取值时，其对应的流量和密度关系曲线图.

由图2可知，密度较低时，即交通流为自由流时，安全距离参数α取不同的值对路段流量影响不大，各条流密曲线的线性部分重合，这是因为前后车辆的相互影响较小.然而，随着密度的增大，参数α取值越大，对流量的约束越大，α=1时，流量最小.当密度ρ达到堵塞密度(0.133 vel/m)时，流量q均为0.

4 实际交通流综合分析

4.1 基于实验数据的交通流时序特性

实际上，道路安全距离参数α的设置是有必要的，笔者以广州天河北龙口西路口的实时交通流数据为基础，根据实际路段交通流的时序特性进行仿真结果与实际交通流的综合比较.

数据采集地点为龙口西路口东进口，其中选用2009年10月28日～10月30日3天全天的数据，由于交通流密度不易采集，实验中由交通流时间占有率线性地替代.如图3(a)、3(b)、3(c)所示为东进口中间的直行车道28日、29日与30日的交通流散点分布图，横坐标为时间占有率Occ，纵坐标为绿灯流率Qg(辆/s).

图3 交通流Qg-Occ散点分布图

4.2 仿真结果与实时时序特性综合分析

为了进行改进CA模型仿真结果和实验现场数据的综合比较，首先利用式(1)进行密度和占有率的换算.比较结果如图4所示，黑色曲线为α=1的仿真结果，其余的散点为实验数据.

图4(a) 直行车道(中间车道) 图4(b) 直右车道

由图4可知，CA模型仿真得到的流密变化规律和实际交通流是相似的：总体变化规律都近似抛物线型，而在自由流时段流量密度都近似线性关系，但是两者的结果还是有很明显的差别，这是因为现实中交通流的干扰因素很多，如相邻车道车辆、红绿灯、行人等影响导致流量不能达到理想值就掉下来了，且分布比较离散.此外，在速度波动较大的情况下，密度和占有率的换算有较大误差.因此，在路口停车线上，相较于参数α的其它取值，α=1是更为合适的.

5 结束语

城市交通流的元胞机模型是基于车辆和驾驶员个体行为的学习，文中模型规则的改进考虑了车辆的慢启动效应，引进了安全距离参数α，使其模型更加切合实际交通流的运行机理，因此可以较真实地再现交通流现象.最后，基于实验交通流数据的时序特性分析验证及安全距离参数的研究使其更具有现实意义.

另一方面，由于实际交通流受到的干扰因素较多，使得模型仿真结果与现实数据有一定的差别.在今后的工作中应多考虑其它因素对交通流的影响，使模型更切合实际交通流.

参考文献

[1] 周成虎. 地理元胞自动机研究[M]. 北京：科学出版社， 2006：1-17.

[2] M.E. La′rraga, J.A. del R1′o, L. Alvarez-lcaza. Cellular automata for one-lane traffic flow modeling[J]. Transportation Research， 2005，(13)：63-74.

[3] Junfang Tian, Bin Jia, Xingang Li，etal. Synchronized Flow in a Cellular Automata Model with Speed Variation Dependent Randomization[C]. 2009 Fifth International Conference on Natural Computation，2009：433-437.

[4] 靳文舟，张 杰，郑英力. 基于细胞自动机理论的交通流模拟模型[J]. 华南理工大学学报(自然科学版), 2001，29(8)：93-96.

[5] 王殿海，严宝杰.交通流理论[M].第一版.北京：人民交通出版社，2002.

[6] Nagel, K., Schreckenberg, M. Cellular automaton models for freeway traffic[J]. Physics I,1992,(2)：2 221-2 229.

[7] S.C.Benjamin, N.F.Johnson and P.M.Hui. Cellular automaton models of traffic flow along a highway containing a junction[J]. J.Phys., 1996,(A29)：3 119-3 127.

[8] M.Rickert, Nagel, Schreckenberg. Two lane traffic simulations using cellular automata[J]. Physica A, 1996，(231):534-550.

[9] 贾 斌,高自友.基于元胞自动机的交通系统建模与模拟[M].北京：科学出版社,2007.

[10] 贺国光，冯蔚东.ITS与自组织理论[J]. 公路交通科技, 1998,15(3):8-12.