吸振器原理在离心脱水机改进设计中的研究

原 霞， 樊文欣 ， 李保集

(1.中北大学机械工程与自动化学院， 山西 太原 030051； 2.太原生产力促进中心， 山西 太原 030009)

0 前 言

离心脱水机是利用离心运动把物料中的水分脱离出去[1]，其工作时是将物料放在筛篮、筛网或分离转筒里，当转的比较慢时，水滴跟物体的附着力足以提供所需的向心力，使水滴做圆周运动；当转的比较快时，附着力不足以提供所需的向心力，于是水滴做离心运动，从而实现水分和物料分离.离心脱水机广泛应用于煤炭、化工、冶金等行业，锥形筛篮是离心脱水机关键部件之一.

1 振动控制的分类及采用的措施

剧烈的振动常常会损害结构物的强度或妨碍机器的正常功能，还会使机器的联接件产生松动，从而影响加工精度.本文所研究的某新型卧式振动离心脱水机其主要技术采用非线性惯性振动系统排料，双电机驱动强迫同步振动器激振，筛篮主轴和两激振主轴的支承轴承采用3个独立的油腔浸油润滑，并采用橡胶隔振器，同时筛篮和大皮带轮与筛篮主轴间均采用胀套联结.该新型卧式离心脱水机在使用过程中存在一些问题，主要运动部件振动偏大.

系统受外界振源的激励可产生强迫振动，因而要求避免共振和降低系统的振动水平，同时系统内由于一些耦合作用而产生通常具有发散性的动不稳定性，也会使振动不断扩大，最终导致灾难性破坏，因此必须加以控制和消除：按不同性质的振动分动力响应的控制和动稳定性的控制；按采用的抑制振动的手段分隔振、吸振、消振、阻振和结构修改；按是否需要能源分为无源控制和有源控制.卧式离心脱水机常采用的减振措施有大基础吸振和隔振.针对运动部件振动偏大常用的措施有将离心机机座钢板厚度加厚，加隔振橡胶块后用特制螺栓固定离心机基础；及时更换减振垫和筛网减振弹簧；通过模拟法进行主振弹簧刚度的计算及结构的选取,设计主振弹簧弹性模量及外型尺寸.

2 吸振器原理

如图1中由质量m1和弹簧k1组成的系统是主系统.为了在相当宽的工作范围内使主系统的振动保持在设计要求的范围之内，设计了由质量m2、弹簧k2和阻尼器c组成的系统，称之为有阻尼吸振器.主系统和吸振器组成了一个新的两自由度系统，其运动微分方程为：

(1)

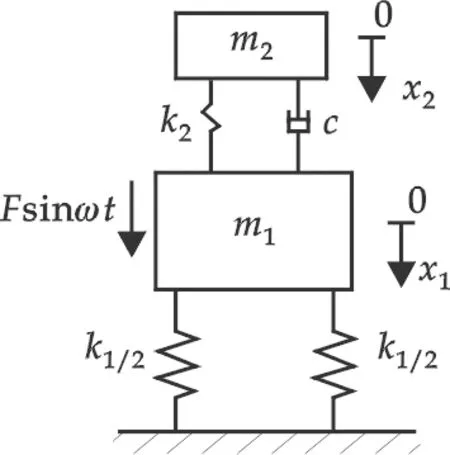
图1 系统的力学模型

(2)

式(2)中a=(k1-ω2m1)(k2-ω2m2)-ω2k2m2，b=ωc(k1-ω2m1-ω2m2).

我们关心的是如何选择吸振器参数m2、k2和c，将主系统在激励力Fsinωt的作用下的稳态响应振幅减小到允许的数值范围内.为了简化讨论，引入下列记号

把式(2)上述符号化为无量纲的形式

(3)

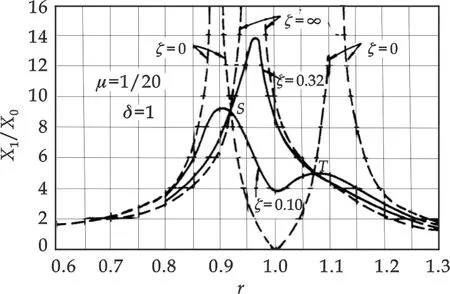
图2 时振幅与r的关系曲线

在图2中，所有响应的曲线都交于S点和T点，表明这两点所对应的频率比、质量m1的稳态响应的振幅与吸振器的阻尼c无关，S点和T点的r值可由任两个不同阻尼值的响应曲线求得.对于工程问题，并不要求使主系统的振幅x1一定要等于零，只要小于允许的数值就可以了.因此，为了使主系统在相当宽的频率范围内工作，我们将这样来设计吸振器：使x1S=x1T，并使x1S和x1T为某个响应曲线的最大值.合理选择和确定吸振器参数，把x1S和x1T控制在要求的数值以内.根据文献[2]可得：

(4)

(5)

(6)

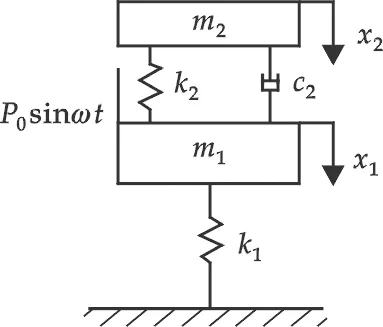
图3 离心脱水机的力学模型

这样可以由主系统允许的最大振动确定μ，从而确定吸振器质量m2；由μ值可得δ，即确定了ω2，从而得到吸振器弹簧常数k2；最后要确定吸振器的阻尼系数c.为使x1S和x1T为响应曲线的最大值，则应在响应曲线的S点和T点有水平切线，从而可得相应的ζ值.

3 某离心脱水机的改进设计

3.1 模型的建立

3.1.1 力学模型的建立

从某离心脱水机的结构图结合振动的有关理论可建立其力学模型,如图3所示.

3.1.2 数学模型的建立

(7)

3.1.3 由数学模型求解主质量和辅助质量的相对振幅

根据以下公式计算：

(8)

(9)

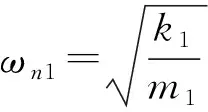
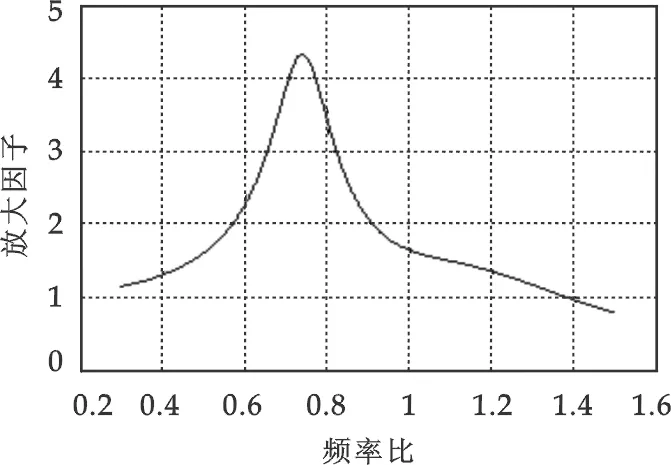
图4 放大因子与频率比的关系曲线

3.2 MATLAB仿真分析

3.2.1 对原方案进行仿真分析

对离心脱水机原设计的参数利用MATLAB语言编程可得主系统的运动曲线如图4所示[4].

从图4可以看出：该离心脱水机工作在一个较窄的减振带内，且其振幅变动较大.

3.2.2 改进方案的仿真分析

不同阻尼比ζ的所有曲线都经过S、T两点，因此这两点的位置与阻尼比无关.为了保证减振器在整个频率范围内都有较好减振结果，应使S、T两点的纵坐标相等，而且成为幅频响应曲线的最高点，在不改变原有质量比μ的条件下，根据式(10)选择最佳频率比αop和最佳阻尼比ζop，即可达到此要求.

(10)

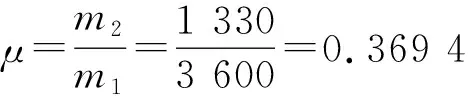
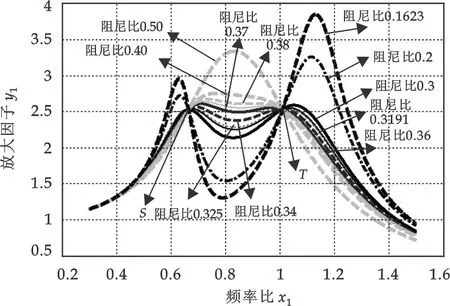
图5 不同ζ下放大因子与频率比的关系曲线

图5给出了在μ=0.369 4，最佳频率比αop=0.73的情况下不同ζ下放大因子与频率比λ的关系曲线.

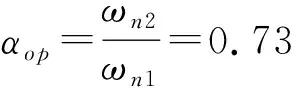
3.3 改进措施

在保持辅助质量和主质量之比μ=0.369 4不变，由经验公式求得最佳频率比αop=0.73和较佳阻尼比ζop=0.319 1，对0.319 1附近不同的阻尼比ζ进行仿真，结果如图5所示.从图中可以看出在阻尼比ζ=0.36～0.38范围内，系统振幅变化较小，并且可以在较宽频带范围内工作，故在橡胶块的布置形式及型号、数量已经确定的情况下橡胶块的刚度k和系统阻尼比ζ均与橡胶块的参数有关，我们可以在保证k1不变的情况下，通过改变橡胶块的长、宽来改变k2，使系统的刚度比达到0.213 4，使阻尼比接近并达到0.36～0.38，从而使橡胶阻尼吸振器达到预期的效果.

4 结束语

本文运用吸振器原理对某离心脱水机进行了振动分析，建立了其物理模型和数学模型，并应用MATLAB进行了编程、仿真，在保持原有结构和质量不变的基础上，通过调节橡胶块设计参数，使得主系统和辅助系统的刚度比及阻尼比达到最佳，从而使主系统振幅达到最小，为离心脱水机的改进设计提供了理论参考.

参考文献

[1] 石年勋. 离心机的振动与隔振技术分析[J]. 过滤与分离，1996，(2)：27-31.

[2] 程耀东. 机械振动学[M].杭州：浙江大学出版社，2002：59-65，117-120，126-131.

[3] 张英会，刘辉航，王德成.弹簧手册[M].北京：机械工业出版社，2002.

[4] 尚 涛，石端伟，安 宁，等.工程计算可视化与MATLAB实现[M].武汉：武汉大学出版社，2002.

[5] 方子良. 动力减振器最佳参数的确定方法[J]. 南京理工大学学报，2002,(3)：334-336.

[6] 邵燕祥，朱海龙.TLL-700离心脱水机的故障分析和解决方法[J].选煤技术，2005,(1)：30-31.

[7] 雷国黔, 宋高东.TZ-14离心脱水机故障处理方法[J].选煤技术，2007,(6)：39-41.

[8] 冯朱涛, 赵艳平.卧式振动离心机与立式刮刀离心机比较及故障分析[J].煤矿机械，2008,(9)：207-209.

[9] 卢国斌.WZL1200卧式振动离心脱水机研制开发[J].山西焦煤科技，2009,(4)：9-11.