机床空间位置误差平面光栅测量补偿及实验验证

王林艳, 沈云波

(西安工业大学机电工程学院， 陕西 西安 710032 )

0 引言

由于机械零件精度和表面加工质量提高的一致性要求，高精度数控加工中心在现代制造业中得到了越来越广泛的应用.数控机床的运动精度是影响机械零部件加工质量的一个主要方面[1].一般认为，数控机床的位置误差主要是由机床的几何误差、切削力及动态载荷等引起的，几何误差是其主要方面[2,3].

许多研究者针对不同误差测量设备和数控机床的类型，提出了相应的几何误差模型和位置误差补偿模型，对提高数控机床的加工精度具有一定的意义[4-6].平面正交光栅由德国生产， 1996年日本首先将该设备应用于机床的运动精度诊断[7]，其特点是分辨率高、非接触测量，可应用于空间任一平面内的运动，对相对运动速度约束较少.本文首先分析了正交光栅的工作原理；其次建立了三坐标立式加工中心空间位置误差的数学模型，并应用人工神经网络技术建立了误差补偿模型；最后通过实验对补偿模型进行了验证，并给出了结论.

图1 正交光栅测量原理图

1 平面正交光栅测量原理

图1为平面正交光栅测量原理图.

平面光栅直径一般为140～230 mm，工作时将光栅水平或垂直安置在NC机床的工作台上，读数头安装在机床的主轴上，使两者间隙为4 mm.NC机床以工作状态使读数头相对平面光栅做恒间隙运动，模拟加工时的进给运动.利用光的衍射原理，通过读数头直接读出运动轨迹位置的精确信号，其读数分辨率可达5 mm[8].

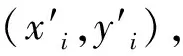
(1)

2 空间位置误差模型

空间位置误差与各几何误差分量之间的关系可通过一个刚体模型、误差的小角度近似和齐次坐标变换得到，本文在参考文献[5，9]几何误差模型的基础上，建立了立式加工中心沿三坐标轴方向空间位置误差模型：

Δx=δX(x)+δX(y)-δX(z)-(TZ+z)Φzx+εZ(z)Ty-εY(z)Tz-(wY+y)ΦXY-(εZ(x)+εY(y))wz

(2)

Δy=δY(x)+δY(y)-δY(z)+(TZ+z)ΦYZ-εZ(z)Tx+εx(z)TZ-(εX(x)+εY(y))wZ+(εZ(y)+εz(x))wx+εz(y)x

(3)

Δz=δZ(x)+δZ(y)-δZ(z)+εY(z)Tx-εx(z)TY-(εX(x)+εY(y))wX+(εX(y)+εX)(x))wY-εY(y)x

(4)

其中:δ为位移误差，下标表示导轨的运动方向，括号内x,y,z表示误差的方向；ε表示绕X、Y、Z轴的回转误差，下标表示导轨的运动方向，括号内x,y,z表示误差的方向；Φxy，Φyz，Φzx分别为X与Y、Y与Z、Z与X导轨之间的垂直度误差；[Tx,Ty,Tz]为刀具的刀尖点在坐标系中的坐标矢量；y，x，z为工作台、滑台和主轴分别沿Y，X，Z轴移动的距离；[wx,wy,wz]为工件在坐标系中的坐标矢量.

由文献[9]可知，各单项误差可表示为机床位置(x,y,z)的非线性函数，所以仅考虑XY平面时空间位置误差表示为：

(5)

XZ平面空间位置误差表示为：

(6)

YZ平面空间位置误差表示为：

(7)

α,β,γ为坐标系中X,Y,Z对应坐标轴之间的偏离角，αij,βij,γij为多项式系数.由以上3式看出，位置误差Δx,Δy,Δz分别是机床运动位置x,y,z的非线性函数，在不考虑其它因素影响的情况下，可以把以上3式写成如下形式.以XY平面为例有:

Δx=fxy(x,y)Δy=gxy(x,y)

(8)

可以看出，求解以上各式系数的方法解出函数的具体表达式是非常困难的.通过对人工神经网络技术研究表明，人工神经网络具有在事先不知道确定函数形式的情况下进行非线性影射的特性.因此，利用人工神经网络技术影射上述的非线性函数关系，确定空间位置误差与机床运动位置的对应关系.

3 神经网络误差补偿模型

3.1 神经网络误差补偿模型的建立

用平面正交光栅测量数控机床误差，是按一定的坐标位置间隔离散地检测出各空间点误差的大小.补偿时，通常采用测量误差值取反叠加.对于未测量点的误差，目前主要采用查表法或插值法来确定[10].但由于实际测量的空间误差数据中总是或多或少地存有噪声，利用这些误差数据直接进行补偿或线性插值时，等于叠加了噪声而没有均化噪声，因此其补偿后的结果往往波动利害、泛化性不好，影响到误差补偿的精度[11].利用神经网络技术建立空间误差补偿模型，实践证明该模型可有效地对样本数据进行滤波、弱化噪声干扰，所期望数据的精度在允差要求的范围之内.神经网络误差补偿模型如图2所示.

模型中输入节点为2个，对应输入向量(x,y).输出节点是1个，对应空间位置误差Δx或Δy.中间隐含层节点为11个(由实验获得).这3层之间节点实行全连接，即左层每一个神经元节点与右层每一个神经元节点都有连接.同一层间的神经元节点没有任何连接.wi,j为输入层到隐含层的权值向量，wj,k是隐含层到输出层的权值向量.隐含层各单元节点采用Sigmoid激活函数为:

(9)

输出层节点的激活函数为线性函数：

Φ(v)=v-1≤v≤1

(10)

图2 神经网络误差补偿模型 图3 误差补偿原理

3.2 误差补偿原理

利用已经训练过的神经网络模型对已测量点和未测量点进行误差仿真，仿真的结果作为该点进行补偿的数值.再将该误差数值取反后叠加到数控指令代码中进行数控加工程序的重构，生成新的数控指令代码，使CNC控制器作出相应动作以达到误差补偿的目的,其原理如图3所示.

4 空间位置误差测量及补偿

4.1 实验设计及测量结果

主要设备有：平面正交光栅测量系统(直径为230 mm)、三坐标立式加工中心、千分表、计算机等，误差测量实验装置如图4所示.

图4 机床误差测量装置 图5 测量刀具轨迹

实验是在空载的条件下进行的.为了验证需要，将设计点和预测点的坐标一并测出(图中56个实心圆点表示测量点，其余点为预测点).测量轨迹、X方向Y方向空间位置误差、剖面线误差分别如图5、6和7所示.

为了保证实验数据的有效性和可验证性，研究机床运动速度对空间位置误差的影响，分别在机床转速为500 mm/min、1 000 mm/min和1 500 mm/min 3种情况下重复进行实验.同时，为了消除随机误差给测量结果带来的影响，对每一个目标点及其附近的样本数据在一定的误差范围内做平均滤波，其结果作为该目标点的坐标值.由图6(a)和7(a)可看出曲面上沿X向的位置误差一般在-2.5～+1 μm之间.由图6(b)和7(b)可看出曲面上沿Y向的位置误差一般在-1.0～+3.0 μm之间.机床运动速度对结果影响不大.

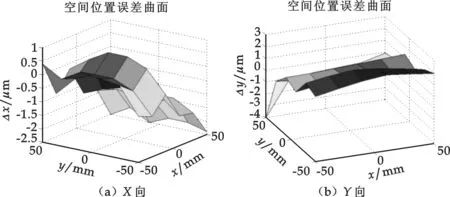
图6 X、Y向空间位置误差

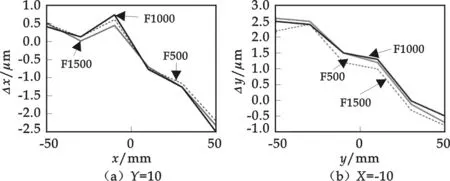
图7 沿Y=10 、X=-10的误差曲线

4.2 未测量点空间位置误差仿真

按照一定的规则选择其中的56个点作为输入样本(图5实心圆点所示)对神经网络误差补偿模型进行训练，其它65个点用训练好的网络权值进行误差预测(仿真).预测结果如图8所示，与图6对比表明预测结果与实际测量值反映的误差分布趋势一致.

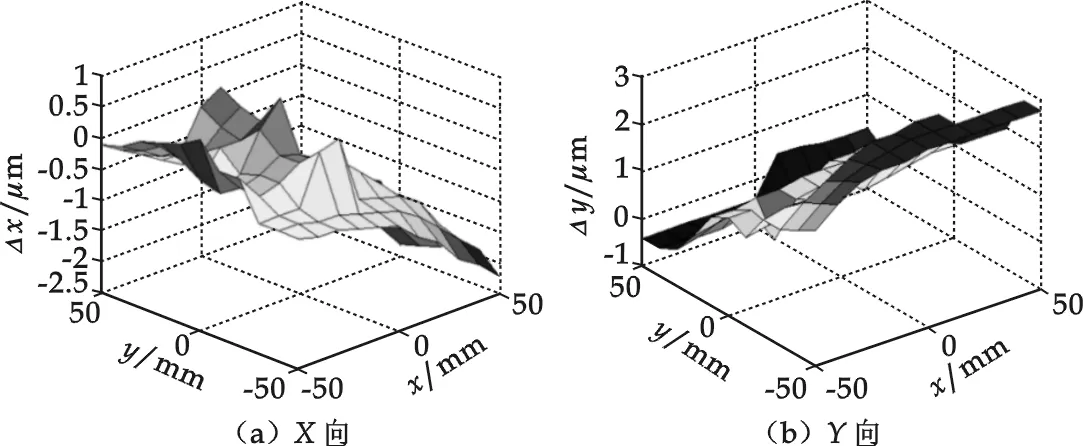
图8 X、Y向预测结果

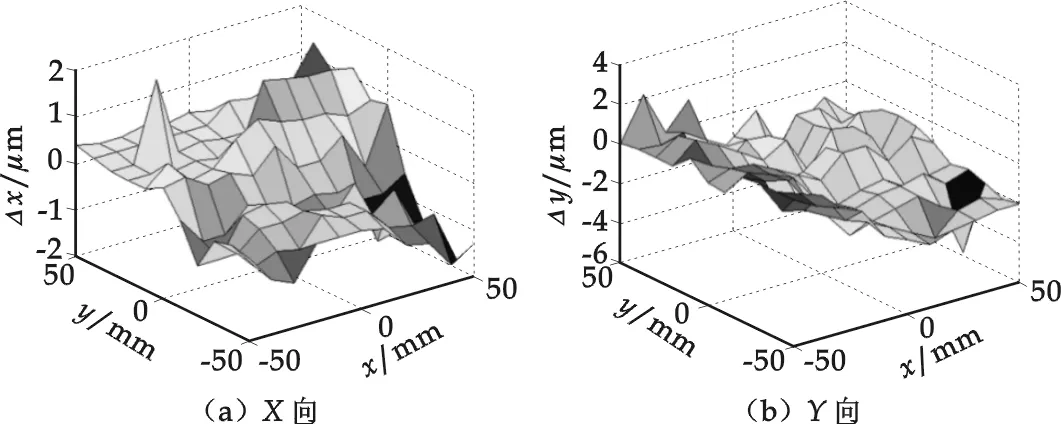
图9 补偿后X、Y向空间误差

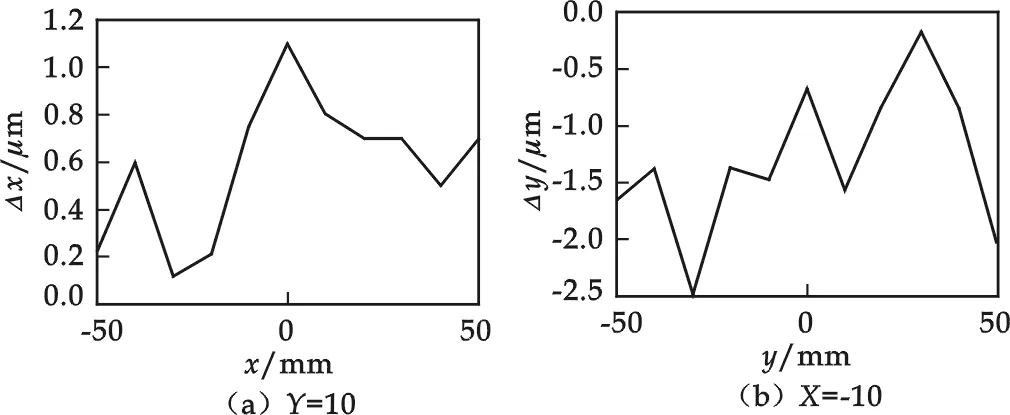
图10 补偿后沿Y=10、X=-10的误差曲线

4.3 误差补偿结果

根据误差补偿原理，将实际测量误差值(经滤波处理)和误差预测值取反后叠加到目标点上，形成新的数控指令加工程序驱动机床运作，测量补偿后目标点的空间位置误差分布如图9所示，剖面线误差如图10所示.

一次补偿后沿X向、Y向的位置精度有一定改善，位置误差分别控制在-1～+1.2 μm和-2.5～0 μm范围内，拟合后的误差曲面总体变化比较平缓.

5 结束语

利用平面正交光栅检测数控加工中心空间位置误差的方法，建立了空间位置误差与各几何误差分量之间函数关系的数学模型；利用人工神经网络技术建立了三层机床离线位置误差预测模型，对机床未测量点空间位置误差的大小进行了预测；设计了实验项目和实验过程，通过实验验证了该测量方法和补偿模型的正确性，有效地提高了机床空间位置的定位精度.

[1] Chana Raksiri,Manukid Parnichkun.Geometric and force errors compensation in a 3-axis CNC milling machine[J].International Journal of Machine Tools & Manufacture，2004，44：1 283-1 291.

[2] R.ramesh,M.A.Mannan,A.N.Poo.Error compensateion in machine tools-a review part 1:geometric,cutting-force induced and fixture dependent errors[J].International Journal of Machine Tools & Manufacture，2000，40：1 235-1 256.

[3] M.Rahman,J.Heikkala,K.Lappalainene. Modeling measurement and error compensateion of multi-axis machine tools.part 1: theory[J]. International Journal of Machine Tools & Manufacture,2000,40:1 535-1 546.

[4]A.C.Okafor, Y.M.Ertekin.Derivation of machine tool error models and error compensation procedure for three axes vertical maching center using rigid body kinematic[J]. International Journal of Machine Tools & Manufacture,2000,40:1 199-1 213.

[5]K.G.Ahn,D.W.Cho.Proposition,for a volumetric error consideration backlash in machine tools[J]. The International Journalof Advanced Manufacturing technology,1999,15:554-561.

[6]Kakino Y. Accuracy Inspection of NC Machine Tools by Double Ball Bar Method[M].Hanser Publishers,1999:5-58.

[7]刘又午，章 青，王国锋．数控机床误差补偿技术及应用发展动态及展望[J]．制造技术与机床， 1998，30(12)，5-8.

[8]洪迈生,苏 恒.数控机床运动误差检测技术[J].组合机床与自动化加工技术,2002,(1):46-49.

[9]张 虎，周云飞，唐小琦,等.数控机床空间误差球杆仪识别和补偿[J].机械工程学报，2002，38(10)：108～113.

[10]Ford D.Compensation algorithms for the real-time correction of time and spatial encoredr in a vertical machine center[J]. Proceedings of Institution of Mechanical Engineers，2002，2(24):58-62.

[11]董晨松.三坐标测量机动态误差补偿的研究[D].天津: 天津大学博士学位论文，1999：52-64.