各向异性介质椭球内电场的研究

李应乐，王明军，董群峰

（咸阳师范学院，陕西 咸阳 712000）

研究球类目标体系的电磁散射特性及其应用受到国内外学者的普遍关注。单个各向同性球体目标的内外电场问题已被很好解决[1—4]，在平面电磁波沿x 方向极化、z 方向传播时介质球和导体球目标散射特性已有详细的报道[3—5]，文献[6]研究了球体目标对任意入射、任意极化的平面电磁波的散射，文献[7—9]利用尺度分析法和曲面坐标系分别研究了平面电磁波沿x方向极化、z方向传播时椭球目标的电磁散射。同时，文献[10]将高斯波束展为球矢量函数，利用Mie理论研究了高斯波束对双层球形目标的辐射俘获力；文献[11]采用了与文献[10]大致相同的方法讨论了球形目标体系的高斯波束散射特性；Holler等[12—13]研究了球形目标群对高斯激光脉冲的散射、吸收特性；金亚秋等[14—16]研究了分层随机球体目标群对平面波和高斯波束的散射等特性。然而有关各向异性介质椭球目标体系的电磁散射等研究还不尽人意，主要的困难是在各向同性条件下引入的有关辅助位函数在各向异性条件下不能成立，而且描述目标的电磁参数张量因坐标系的变化而变化。有研究表明，如果已知任意形体的各向异性目标内的电场[3]，那么该目标的散射问题已被确定。基于电磁场的多尺度变换理论，将各向异性椭球目标重整为各向同性椭球目标，可得出各向异性介质椭球内电场的解析表达式；对其正确性进行了检验，对介电常数张量、椭球形状参数对球内电场的影响进行了仿真计算，结果为研究各向异性椭球目标的瑞利散射特性提供了理论支持。

1 各向异性介质椭球内电场的研究

1.1 各向异性椭球的重建

设一个半长轴分别为a，b，c 的各向异性介质椭球，球心位于主坐标系的原点，介电常数为：

椭球方程为：

式中：ε1，ε2，ε3为相对介电常数，无量纲。在主坐标系中电势u满足方程：

对式（2）作如下变换：

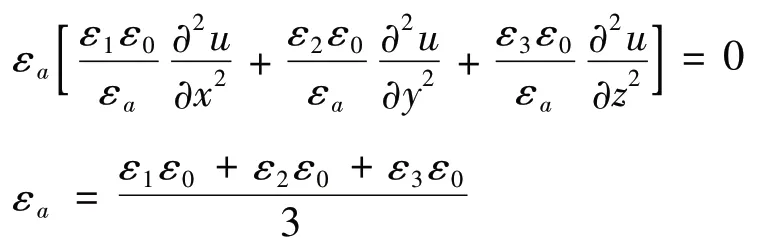
引入新的尺度坐标系，该坐标系中的坐标参数为x′，y′，z′，与主坐标系的坐标参数的关系为：

将上式代入式（2）得电势在尺度坐标系中的微分方程：

在式（3）中利用了尺度坐标系中的电势u′与主坐标系中的电势u 相等这一特性（见文献[8—9]）。式（3）表明：经历多尺度变换后，主坐标系中各向异性的介质目标在尺度坐标系中已被重建为各向同性的介质目标，从而使有关问题的求解简化。重建后椭球方程式（1b）变为：

1.2 各向异性介质椭球内电场的求解

设外电场强度在主坐标系中的大小为E0，方位角为θ0，φ0。该电场在主坐标系的主轴分量分别为：

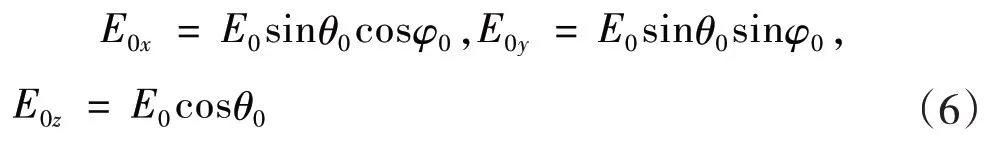
由于在对目标重整的过程中引入了新的坐标，测量的4 个基本量之一长度发生了变化，定义在主坐标系中的电场强度大小在尺度坐标系中必然发生改变；由文献[8—9]主坐标系中电场强度与尺度坐标系中电场强度之间的关系，易求得在尺度坐标系中外电场的分量为：

由文献[2—3]可知，一个各向同性的相对介电常数为εra=εa/ε0的椭球目标的内电场与外电场的关系为：

适当地调换a′，b′，c′就可以得到E′y，E′z分量的表达式，形状因子Ly，Lz，Lx，满足Ly+Lx+Lz= ；式（8）是尺度坐标系中椭球目标内部电场的表达式，在主坐标系中椭球内部的电场为：

同理可得：

式（11）和式（10）分别是各向异性椭球目标内部电场在不同方向的表达式，由此可得椭球内部的总电场与外电场之间夹角β的余弦函数为：

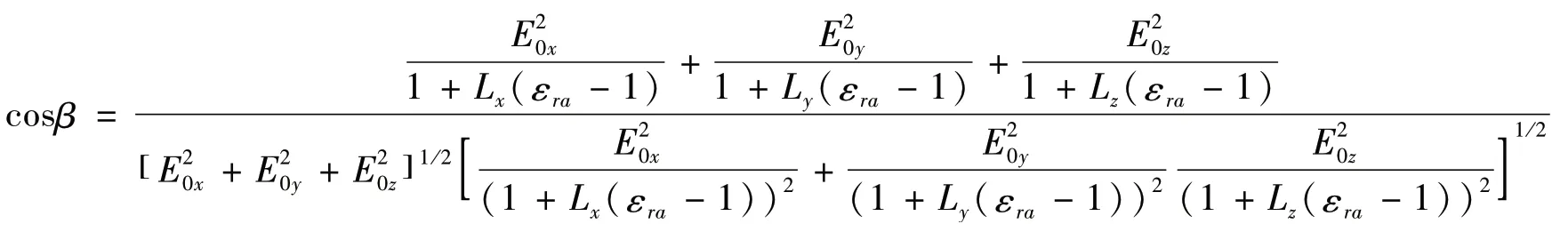
当椭球为各向同性椭球时，即ε1=ε2=ε3=εr，由εa的定义及式（5）可知：

εra=εr， a′=a， b′=b， c′=c

此时，式（11）和式（10）分别变为各向同性椭球目标内部电场在不同方向的表达式，与文献[2—3]结果完全一致，以x分量为例，即：

当a =b=c=R时，椭球将变为球形目标，Lx变为：

式（14）与现有文献结果也完全一致。选择椭球形体参数a=1 m，b=1.5 m 和c=2 m，部分仿真结果如下：图1是外场方位角为θ0=π/6，φ0=π/4时总电场的大小随介电常数张量的变化。介电常数张量元素越大，内场越小。由于各向异性椭球的内电场是外电场与附加电场的叠加，附加电场与外电场的方向相反，正比于极化强度矢量的大小，而极化强度矢量的大小正比于介电常数的大小。图2所示为电场强度的大小随入射角的变化，在φ0一定的条件下，总场随θ0的变化呈现出非线性，在θ0=π/2 时达最大值。在θ0一定的条件下，随φ0的增大而减小，这是由于当方位角θ0=π/2，φ0=0外电场在坐标轴z方向上的分量最小，而该方向的介电常数又最大，从而导致总的极化强度矢量最小。由此可以推出：当外电场与某一坐标轴重合时，各向异性椭球的内场将达到极值分布。图3为各向异性椭球内部电场的方向与外电场方向之间的夹角随介电常数张量的变化。显然，介电常数越大，它们之间的夹角也越大，但最大值不会超过2°；由于介质是各向异性介质，介电常数越大，介质极化后产生的电偶极矩越大，产生的附加电场越大，从而对总场方向的改变也越大。图4表明：夹角β随外电场方位角的变化而变化，但变化范围较小，在近似计算中可以认为夹角β不随外电场方位角的变化而变化。但是夹角β随外电场方位角的变化而变化也表明了目标的电磁各向异性特性。

2 结论

图1 电场强度随介电常数张量的变化Fig.1 The change of electric field with dielectric constant tensor

图2 电场强度随入射角的变化Fig.2 The change of electric field with incident angle

图3 夹角β随介电常数张量的变化Fig.3 The change of angle β with dielectric constant tensor

图4 夹角β随入射角的变化Fig.4 The change of angle β with incident angle

研究了外电场中一个各向异性的介质椭球目标内电场的分布规律；从电磁场的多尺度变换理论出发，对各向异性椭球目标的电磁参数和形体进行重整，得出了各向异性介质椭球内电场的解析表达式，将所得结果退化到各向同性介质中时，与文献所得结果完全一致。计算了椭球内电场方向与外电场方向的夹角，仿真计算了入射场方位角、各向异性介质电参数对椭球内电场方向与大小的影响，结果表明：入射电场的方向对椭球内电场的大小和方向影响不大，介电常数对椭球内电场的方向和大小有较大的影响。由于许多目标都呈现出电磁各向异性，因此所得结果为研究目标Rayleigh 电磁散射等奠定了理论基础。

[1]郭硕鸿.电动力学[M].北京：高等教育出版社，1982：66—70.

[2]STRATTON J A. Electromagnetic Theory [M]. New York：McGraw-Hill，1941：20—50.

[3]ISHIMARU A.Wave Propagation and Scattering in Random Medium[M].New York：Academic Press，1978：27—30.

[4]JIN A K.Electromagnetic Wave Theory[M].Beijing：Publishing House of Electronics Industry，2003：452—457.

[5]王一平，陈达章.工程电动力学[M].西安：西安电子科技大学出版社，1985：308—311.

[6]LI Ying-le，HUANG Ji-ying. The Scattering Fields for a Spherical Target Irradiated by a Plane Electromagnetic Wave in an Arbitrary Direction [J]. Chinese Physics，2006，15（2）：281—285.

[7]LI Ying-le，HUANG Ji-ying.The Accurate Solution of Scattering Field for a Dielectric Ellipsoid[J].Journal of Electromagnetic Waves and Application，2003，17（12）：1745—1754.

[8]LI Ying-le，HUANG Ji-ying. The Scale Transformation of Electromagnetic Theory and Applications[J].Chinese Physics，2005，14（4）：646—656.

[9]李应乐，黄际英.电磁场的多尺度变换理论及其应用[M].西安：西安电子科技大学出版社，2006：30—50。

[10]韩一平，杜云刚，张华永.高斯波束对双层粒子的辐射俘获力[J].物理学报，2006，55（9）：4557—4563.

[11]白璐，吴振森，陈辉，等.高斯波束入射下串粒子的散射问题[J].物理学报，2005，54（5）∶2025—2030.

[12]HOLLER S.Observations and Calculations of Light Scattering from Clusters of Spheres [J]. Applied Optics，2000，39：6873—6887.

[13]VICTOR J，NESATY Y，JULIA L.Dissociation of Non-covalent Protein Complexes by Triple Quadrupole Tandem Mass Spectrometry：Comparison of Monte Carlo Simulation and Experiment[J]. International Journal of Mass Spectrometry，2002，221：245—262.

[14]YA Q. Polarimetric Scattering from a Layer of Random Clusters of Small Spheroids [J]. IEEE Trans on Antennas Propag，1994，42：1138—1144.

[15]LOIC M，GERARD G. Scattering of Laser Pulses（Plane Wave and Focused Gaussian Beam）by Spheres [J]. Appl Opt，2001，40（15）：2546—2550.

[16]GALDI V. Multifrequency Reconstruction of Moderately Rough Interfaces via Quasi-ray Gaussian Beams [J]. IEEE Tran Geoscience & Remote Sensing, 2002，40（2）：453—460.