三频卫星信标测量TEC方法探讨及数值模拟

赵海生，许正文，吴健，於晓

（中国电波传播研究所，山东 青岛 266107）

自1986 年Austen 等提出层析技术应用于电离层研究以来，电离层层析成像技术（Computerized Ionospheric Tomography，简称CIT）取得了重要进展，正在成为一种重要的空间探测手段，业已取得的试验结果表明它是监测大范围电离层结构和扰动的有力手段[1—4]。电离层CIT技术的问世与发展为全球大气监测和其它空间区域遥测技术提供了有益的启示，在某些实用领域，如通信、导航定位、导弹发射监测以及地震预报等方面，电离层CIT 技术也具有潜在的应用价值。

随着电离层CIT 技术研究的深入，对精度的要求也越来越高。影响其精度的误差源主要有3个方面：电子总含量（TEC）的测量误差、数据采集不完整引起的误差、CIT算法引起的误差。其中TEC测量误差是重要的误差源之一，主要是因为相位积分常数未知，在计算过程中引入假设造成的。为了获得精确的相位积分常数，经过深入研究，得到了许多优秀的算法，如最小曲率法、双站法[5]、多站法[6]等。但是，这些算法都需要假设作为前提，比如水平分层假设、无限薄层假设等，计算精度对电离层CIT 来说还显得过于粗糙，需要进一步提高。近年来，三频卫星信标的成功在轨应用给TEC 精确测量带来了希望。2006 年COSMIC 卫星发射成功，该卫星携带三频信标（Tri-Band Beacon，简称TBB）探测仪，3 个载波分别为150，400，1 067 MHz。据报道该设备能够更加精确地获得射线路径上的TEC，更加有效地探测电离层小尺度扰动[7]。

1 双频信标测量TEC的方法

TEC 测量技术主要有法拉第旋转、差分多普勒和差分群时延等，目前的电离层CIT 试验主要采用差分多普勒技术测量TEC，文中采用TEC 的差分多普勒测量方法。差分多普勒技术基于相移或频移的测量，相位对时间的导数为频率，通常将频移称为多普勒频移，频移对时间的积分为相移。信号的相移和频移是由电波传播光程改变引起的，光程是介质折射指数沿路径的线积分，而折射指数包含电子密度的信息，因此由差分相位可获得有关TEC的信息。

设信标机天线发射两个谐和频率分别为f1和f2的载波，其基频为f0，且f1=，f2=n1n2f0，n1和n2为正整数，则在接收天线处两个频率的频移分别是：

式中：c 为光速；t 为卫星的位置；L1，L2为两个频率的光程。光程表达式为：

式中：μ为折射率；r为地面接收站位置；Ne为电子密度。归一后的差分多普勒频移为：

在实际的卫星接收设备中，接收并经过运算电路得到的差分多普勒频移信号往往要经过一个时间积分运算，以给出两个频率的差分多普勒相位数据。对式（4）进行时间积分得到接收天线处的差分多普勒相位为：

式中：tL为接收机锁定卫星信号的时刻；Φ0为相位积分常数，包含锁定时刻相位的整周模糊度以及发射天线处两个频率信号的初始相位差。Φ0未知，因此接收机给出的φD（t） 实际上是差分多普勒相位数据的相对值。

由于讨论的三频信标位于VHF，UHF和L波段，因此可应用高频近似来处理[8]。一般情况下只要电离层的扰动不是特别强，射线路径可以视作直线[9]，结合式（3）和式（5）可得到[10]：

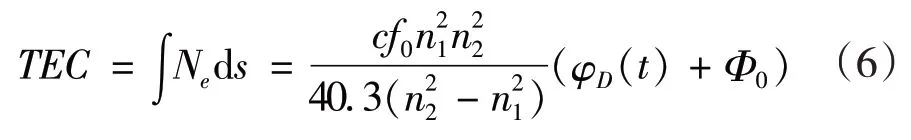
式中：φD（t） 由接收机给出；Φ0可由其他方法计算得到，文中采用多站法[6]求之。

2 三频信标测量TEC的方法

三频信标测量的基本原理见文献[11]。与双频信标相比多了1 个载波ω3将3 个频率载波两两差分可以得到3组双频载波，3组载波利用差分多普勒技术可以得到3个差分相位表达式[11]：

式中：ΔP12，ΔP13，ΔP23为差分相位的绝对值，包含接收机接收到的相对相位和相位积分常数。推导、整理（推导过程详见参考文献[11]）可得到：

式中：n1=3；n2=8；f0=16.668 MHz；mod1 为对1 取模。将其带入式（8）得[11]：

式中：8.316 5×1016为三频信标测量TEC的相位模糊系数；k′为三频相位积分常数，它与双频信标的相位积分常数一样，需要确定。

文中给出了k′的一个有效求解方法，将双频粗测和三频精测结合起来，有效求解了TEC。这种粗测和精测相结合的测量方法，在雷达测距、螺旋测微计测量等方面都有类似的应用。基于此原理设计k′的算法流程如图1所示。

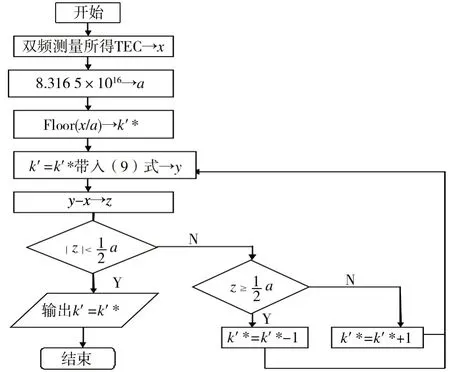
图1 k′计算流程Fig.1 Flow chart of k′calculation

流程图中Floor（x/a）函数为下取整函数。用k′值求得的三频TEC，可以修正误差小于4.16 TECU（TECU 为TEC 的常用单位，1 TECU=1.0×1016个电子/m2）的双频测量结果，双频法的TEC 测量误差在1～3 TECU 量级，可见使用该方法求解TEC 是有效的。下面分别利用双频法和三频法求解TEC，并把求解结果用于电离层CIT成像。

3 数值计算与仿真

无论是双频还是三频求解TEC，只要是用差分多普勒测量技术都无法回避确定相位积分常数的问题。文中采用多站法计算[6]，选取经度120°E，纬度20°～40°N 区域电离层作为测试场景，电离层电子密度由Chapman 模型产生。地面布设6 个接收台站，25°～35°间每2个纬度布设1个台站。卫星高度为500 km，在卫星沿轨道飞越20°到40°之间，每0.5°采1次样。

在仿真模拟时，把加入扰动的Chapman 模型的电子分布，然后按以下方法计算得到实际的TEC 测量值：

式中：TECreal，i为第i条射线的实际TEC值；aij为按照接收机与卫星位置计算得到的路径投影长度；Nej为模型给出的电离层电子密度分布值。

在得到实际的TEC 后，再找出各个地面台站对应所有射线的实际TEC 值的最小值，以此作为实际垂直TEC。将台站所有射线路径上的实际TEC减去实际垂直TEC，即可得到相对TEC 值。以相对TEC值作为实际观测量，按照多站法即可估算各台站的积分常数。计算结果见表1。

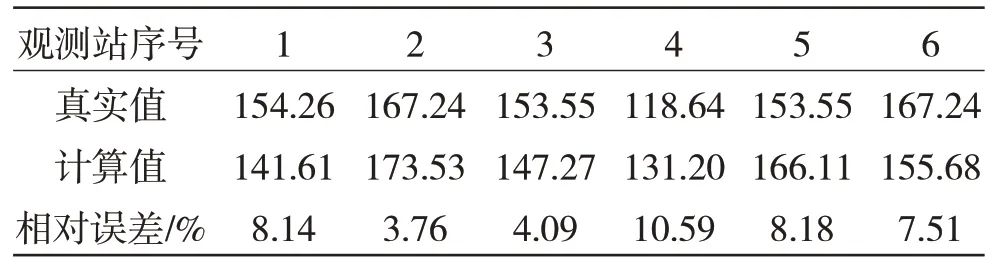
表1 多站法得到的相位积分常数计算值与真实值的比较Table 1 Comparison between the true value and calculated value of integral constant using multi-station method

将求得的相位积分常数带入式（6），可以得到双频信标的TEC，然后按照图1 给出的算法可以求得k′，将k′带入式（9）可以得到三频信标的TEC。将双频和三频得到的TEC，区分为加噪声和不加噪声2种情况，下面用目前最优的MART算法进行电离层CIT重建。

从图2可以看出：在不加噪声的情况下，用三频信标测得的TEC进行CIT反演的结果与模型吻合得很好，能完全重建出模型加入的2个扰动；而双频信标仿真结果失真较为严重，对大尺度扰动，基本可以得到重建；对小尺度虽然还能看出来，但是已无法确定该扰动是由模型引起的还是噪声引起的，甚至在某些局部区域出现了虚假的扰动结构。

图2 不考虑相位测量误差的仿真结果比较Fig. 2 Comparison of simulation results without considering the phase measurement error

以上结果是在不考虑相位测量误差的情况下得到的，而真实情况下由于码元对齐误差、接收机噪声等都可能使相位测量结果存在误差。相位测量误差引起的绝对 TEC 误差一般在 0.1 个 TECU 之内[12—13]，图3 给出的是加入0.1 个TECU 的相位测量误差（该误差在0～0.1 TECU之间随机产生）之后得到的比较结果。

从图3 可以看出加入噪声后，不管是双频还是三频其成像结果变化都不大，可见噪声对成像结果影响有限，说明TEC 的测量误差主要来自相位积分常数的计算误差。从图3 可以明显看出三频的CIT结果与原始扰动模型更为接近，为了进一步量化分析两者的误差情况，为进一步优化算法提供参考，分别将双频和三频的测量结果减去原始扰动模型，取绝对值[14]，其结果如图4所示。

图3 加入相位测量随机误差后的仿真结果比较Fig. 3 Comparison of simulation results with random phase measurement error

图4 误差比较结果Fig.4 Results of the errors comparison

与原扰动模型值相比，双频信标重建结果的电子密度均方根误差为6.934 8×1010，三频信标重建结果的电子密度均方根误差为1.083×1010，从而大大提高了测量精度。

4 结论

在前人给出的三频信标测量绝对TEC原理的基础上，提出了有效的三频信标相位积分常数的求解方法，并用该方法对双频信标计算的TEC 结果进行了修正。采用该方法可以修正误差小于4.16 TECU的双频测量结果。分别将双频和三频得到的TEC作为输入，用MART算法针对不加噪声和加噪声2种情况进行电离层CIT 模拟，结果显示三频信标的成像结果远优于双频信标。特别对小尺度扰动的探测上，三频信标的优势非常明显，这将为地震电磁试验卫星的核心任务之一——用三频信标测量电离层异常变化并较为准确地确定扰动位置打下技术基础。

三频信标测量技术的产生，必将为电离层CIT成像这一新兴的探测技术再次注入活力，未来努力的方向是用实测数据对相关的算法作进一步的研究和分析，逐步形成较高精度的三频信标测量技术，以满足地震电磁试验卫星测量的初步需求。

致谢：感谢中国电波传播研究所的佘承莉和欧明给予的帮助和有益讨论。

[1]TSAI L C，LIU C H.Tomographic Imaging of the Ionosphere Using the GPS/MET and NNSS Data[J]. Atmos Sol Terr Phys,2002，64（18）：2003—2011.

[2]ROGERS N C，MITCHELL C N，HEATON J.Application of Radio Tomographic Imaging to HF Oblique Incidence Ray Tracing[J].Radio Sci，2001，36（6）：1591—1598.

[3]KUNITSYN V E.Tereshchenko Ionospheric Tomography[M].New York：[余不详]，2003.

[4]CANNON P S.Mitigation and Exploitation of the Ionosphere：A Military Perspective[J]. Radio Sci，2009，44：154—158.

[5]LEITINGER R，SCHMIDT G，TAURIAINEN A.An Evaluation Method Combining the Differential Doppler Measurement from Two Stations that Enables the Calculation of the Electron Content of the Ionosphere[J]. Geophys，1975，41：201—213.

[6]叶怡君. 赤道异常区三维电离层之断层扫描模拟研究[D].台湾：国立中央大学太空科学研究所，2001.

[7]ZHAO H S，Z W，XU J.Ionospheric Tomography of Smallscale Disturbances with a Tri-band Beacon：a Numerical Study[J].Radio Sci，2010，45：1029—1031.

[8]KUNITAKE M K，OHTAKA T，MARUYAMA M.Tomographic Imaging of the Ionosphere over Japan by the Modified Truncated SVD Method[J]. Ann Geophys，1995，13：1303—1310.

[9]徐继生，邹玉华，马淑英.GPS地面台网和掩星观测结合的时变三维电离层层析[J].地球物理学报，2005，48（4）：759—767.

[10]吴雄斌.低纬电离层CT试验与算法[D].武汉：武汉大学，1999.

[11]BERNHARDT P A，SIEFRING C L. New Satellite-based Systems for Ionospheric Tomography and Scintillation Region Imaging[J].Radio Sci，2006，41：1029.

[12]闻德保.基于GPS 的电离层层析算法及其应用研究[D].武汉：中国科学院测量与地球物理研究所，2007.

[13]FRIDMAN S V，NICKISCH L J，HAUSMAN M.Personalcomputer-based System for Real-time Reconstruction of the Three-dimensional Ionosphere Using Data from Diverse Sources[J].Radio Sci，2009，44（3）：1256—1261.

[14]PAGE D L. Comparison of Tomographic and Conventional Methods for Resolution of the Constant of Integration[J].Radio Sci，1997，32（4）：1645— 1656.