基于向量通用生成函数的多性能参数多态系统可靠性分析

李春洋，陈循，易晓山，陶俊勇

(国防科技大学 机电工程与自动化学院，长沙410073)

0 引言

系统除了正常工作和完全失效两种状态外，还具有多种工作(或失效)状态，或系统能够在多个性能水平下运行，这样的系统被称为多态系统［1-3］。多态系统一些部件的失效或者性能衰退会导致系统性能的下降，同时引起整个系统呈现出多个性能水平。多态系统可靠性能够详细地、广泛地定义部件和系统的可靠性，能够透彻地分析部件性能的变化对系统性能和可靠性的影响，以及系统失效的渐变过程。

20世纪70年代多态系统的概念被提出之后［4-5］，多态系统可靠性的研究得到了国外学者的广泛关注。多态系统可靠性的相关理论已经应用到电力［6-7］、网络［8-9］和机械［10-11］等领域。我国对多态系统可靠性的研究相对较少，起步也比较晚，主要集中在多态系统可靠性分析［12-14］，多态系统共因失效分析与优化［15-17］等方面。

多态系统可靠性分析主要有4 种方法:布尔模型扩展法［2，18］、随机过程［2，12，14］、Monte Carlo 仿真［19-20］和通用生成函数［1-2，6-8，15-17］。其中，通用生成函数是解决多态系统可靠度计算问题应用较好的方法，它能够明确地表达部件状态性能和对应概率与系统状态性能和对应概率的关系，并且可以通过简单的运算由部件的通用生成函数得到系统的通用生成函数，它具有计算速度快，适用范围广等特点［21］。

Ushakov［22-23］首先介绍了通用生成函数的概念，随后Levitin［1-2］和Lisnianski［2］等学者将通用生成函数引入多态系统可靠性领域，使得通用生成函数在多态系统可靠性分析［1-2，8，15，17，24］和多态系统可靠性优化［1-2，6-7，16，21，25-26］等方面获得了广泛应用。此外，An 和Huang 等利用通用生成函数建立了离散的应力-强度干涉模型［27］，分析了V 带传动的可靠性［28］。

在以上文献中，通用生成函数都是针对离散随机变量，在通用生成函数中体现为单一变量，在利用该通用生成函数分析多态系统可靠性时，部件性能和系统性能都只有一个参数。但在实际工程中，不少系统具有多个性能参数，特别是机电系统。对于具有多个性能参数的多态系统，在利用通用生成函数进行可靠性分析时，需要对离散随机变量的通用生成函数进行改进，以适应实际需要。

针对多性能参数多态系统可靠性分析的需要，本文通过对变量通用生成函数［1-2，21-28］进行改进，提出向量通用生成函数，定义其相应的运算符和基本性质，并且分析利用向量通用生成函数估算多态串-并联系统可靠度的计算方法和详细流程，最后利用由性能退化部件组成的串-并联系统进行应用研究。

1 向量通用生成函数的定义

假设G =(G1，G2，…，Gm)为m 维离散随机向量，其概率分布可以用2 个集合g 和q 描述。其中，g 表示离散随机向量G 的M 个可能取值，有如下形式:

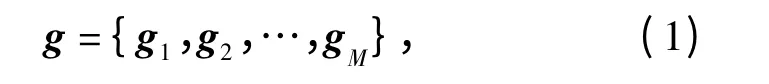
其中，

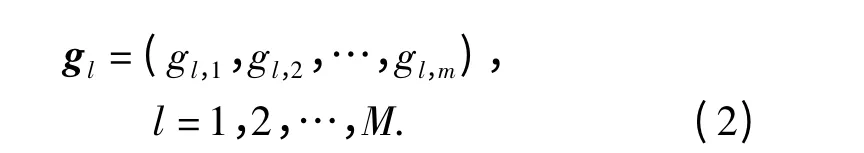
q 表示M 个取值分别所对应的概率，有如下形式:

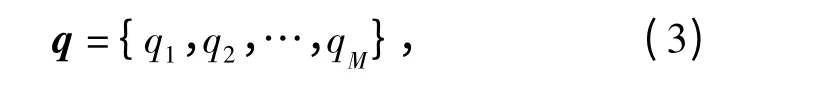
其中，

且满足

则定义离散随机向量G 的向量通用生成函数为

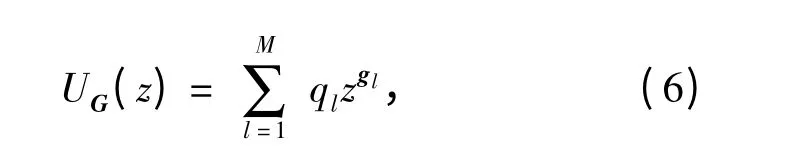
式(6)所定义的向量通用生成函数与变量通用生成函数［1-2，21-28］相比，其最大不同在于式(6)中gl为向量，而变量通用生成函数中gl为变量。在对向量通用生成函数进行计算时，其计算相对比较复杂，特别是当多个离散随机向量的维数不同，且相互之间的关系较为复杂时。

2 向量通用生成函数的运算

2.1 2 个随机向量的函数的向量通用生成函数

定义H =(H1，H2，…，Hm')为m'维离散随机向量，其概率分布可以用2 个集合h 和p 描述。其中，h={h1，h2，…，hM'}表示H 所有可能的M'个取值，且hk=(hk，1，hk，2，…，hk，m')，p ={p1，p2，…，pM'}表示每个取值所对应的概率。则由式(6)知，其向量通用生成函数为

定义m″维离散随机向量D =(D1，D2，…，Dm″)为G 和H 的函数，即D=f(G，H).其中，

式(8)表示Di为Gri(1)，…，Gri(ai)，Hsi(1)，…，Hsi(bi)的函数，即Di为离散随机向量G 的第ri(1)，…，ri(ai)个分量与离散随机向量H 的第si(1)，…，si(bi)个分量的函数。其中，1≤ri(1)＜…＜ri(ai)≤m，ai∈{1，2，…，m}，1≤si(1)＜…＜si(bi)≤m'，bi∈{1，2，…，m'}，i=1，2，…，m″.

则D 的向量通用生成函数可以通过如下复合运算获得

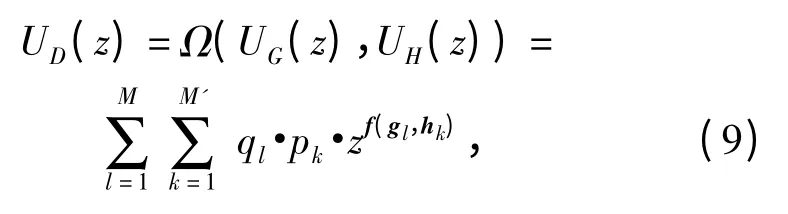
其中，

在计算式(9)时，向量通用生成函数中的同类项可以合并。比如，如果f(g1，h1)=f(g2，h2)，则为了简化计算过程，可以将q1p1zf(g1，h1)和q2p2zf(g2，h2)合并为(q1p1+q2p2)zf(g1，h1).合并同类项之后可以减少离散随机向量的可能取值数，从而减少计算量。

介绍一种常用的特殊情况，当m =m' =m″时，即随机向量维数相同，且式(8)为Di=fi(Gi，Hi)时，则式(10)可以简化为

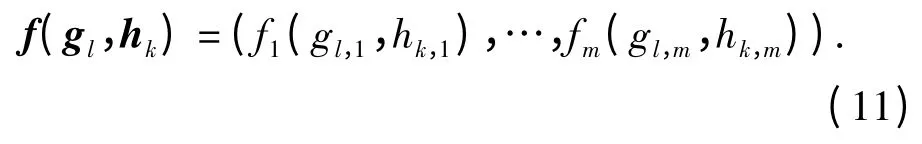
此时，定义如下几个比较常用的算子

2.2 多个随机向量的函数的向量通用生成函数

定义N 个离散随机向量G1，G2…，GN，其对应的向量通用生成函数分别为U1(z)，U2(z)，…，UN(z).则向量函数f(G1，G2，…，GN)的向量通用生成函数为U1(z)，U2(z)，…，UN(z)的复合运算

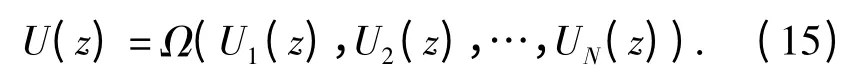
对式(15)进行运算时，要用到向量通用生成函数的如下性质［1-2，27］:

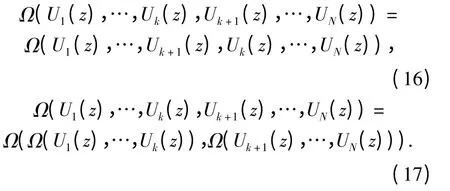
利用以上性质，可以最终得到向量函数f(G1，G2，…，GN)的向量通用生成函数为

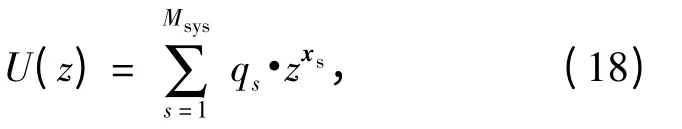
式中，Msys为向量函数f(G1，G2，…，GN)的可能取值数，由于可以合并同类项，故为向量函数f(G1，G2，…，GN)的可能取值，qs为对应的概率。

3 多性能参数多态系统可靠性分析

图1所示的多态串-并联系统由N 个分系统串联组成，其中分系统i 并联ni个部件。设该多态串-并联系统的部件和系统具有多个性能参数。

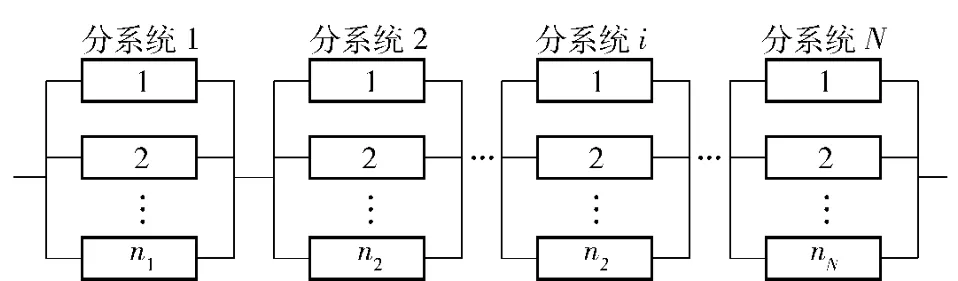
图1 多态串-并联系统Fig.1 Multi-state series-parallel system

计算该系统的可靠度时，有以下几个步骤。

3.1 计算部件的向量通用生成函数

分系统i 的部件j 有Mij个状态，t 时刻部件的状态性能为gij(t)={gij1(t)，gij2(t)，…，gijMij(t)}，对应的状态概率为qij(t)={qij1(t)，qij2(t)，…，qijMij(t)}.则由式(6)，其向量通用生成函数为

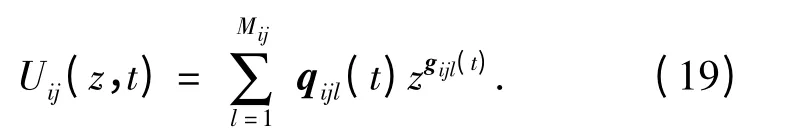
对于离散多态系统，部件的状态性能gij(t)和状态概率qij(t)可以直接得到［1-2］，对于多态退化系统，需要对性能分布进行离散化，离散化时状态数可以根据需要来确定，具体情况在算例中分析。

3.2 计算分系统的向量通用生成函数

分系统i 由ni个部件并联组成，分系统性能可以表示为

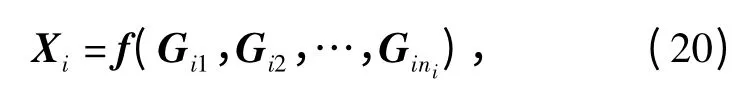
式中，Xi为分系统i 的性能，Gi1，Gi2，…，Gini为部件性能。

式(20)为分系统结构函数，它表示分系统性能与部件性能的关系。

根据部件的向量通用生成函数(式(19))和分系统的结构函数(式(20))，利用式(15)、式(16)、式(17)计算分系统i 的向量通用生成函数为

式中:Mi为分系统i 的状态数;{xi1(t)，…xiMi(t)}为t 时刻分系统i 的状态性能;{qi1(t)，…，qiMi(t)}为对应的状态概率。

在得到了分系统的向量通用生成函数之后，对于并联部件较多的情况，分系统i 的状态数Mi会比较大，为了减少计算量，提高计算速度，采用状态重新划分法进行处理:

将Ui(z，t)的Mi个状态重新划分为M'i个状态，M'i＜Mi，M'i的大小可以根据计算精度和实际需要来确定。重新划分之后，分系统i 的状态性能变为

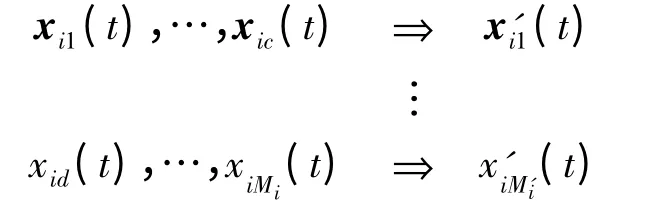
对应的状态概率变为

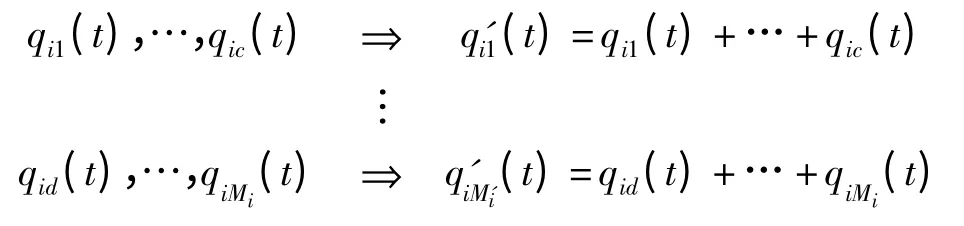
此时，分系统i 的向量通用生成函数为

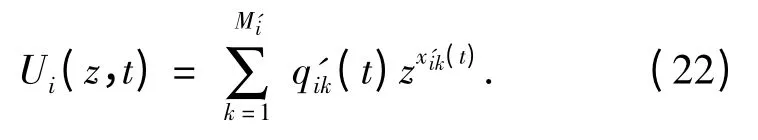
状态重新划分法的应用比较灵活，可以在计算分系统的向量通用生成函数过程中应用，也可以在计算系统的向量通用生成函数过程中应用。

3.3 估算多态系统可靠度

系统由N 个分系统串联组成，系统结构函数为:

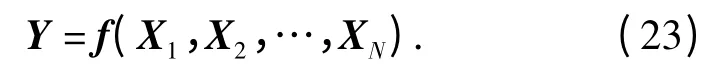
式中:Y 为系统性能;X1，X2，…，XN为分系统性能。

估算多态系统可靠度时，根据系统结构函数的特点，分3 种情况分析。

1)系统结构函数已知

如果系统结构函数已知，系统性能与分系统性能有明确函数关系，那么在得到各分系统的向量通用生成函数之后，利用式(15)、式(16)、式(17)可以得到系统的向量通用生成函数为

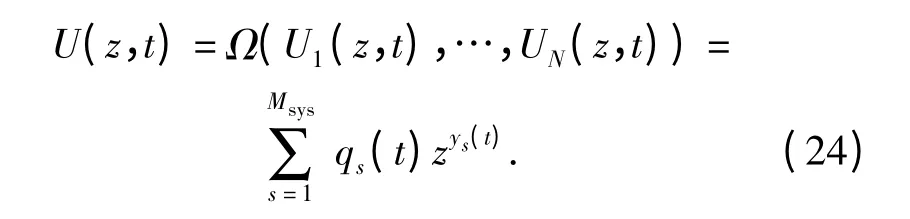
式中，Msys为系统的状态数;{y1(t)，…，yMsys(t)}为t时刻系统的状态性能;{q1(t)，…，qMsys(t)}为对应的状态概率。

不失一般性，设2 个向量Y=(Y1，Y2，…，Ym)和Z=(Z1，Z2，…，Zm)，如果对于所有的i，都有Yi≥Zi，则定义Y≥Z;如果对于所有的i，都有Yi≥Zi，且至少有一个i 使得Yi＞Zi，则定义Y ＞Z.

定义如下运算符

其中，

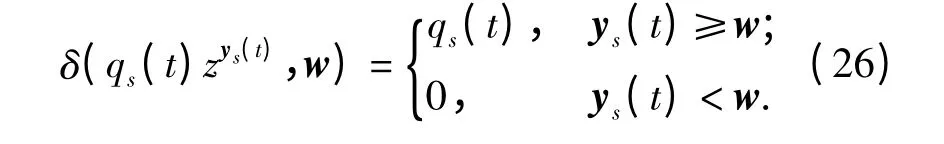
定义w 为系统的最小性能需求，当系统的状态性能不小于w 时，系统可靠，否则，系统不可靠。因此，t 时刻系统可靠度为

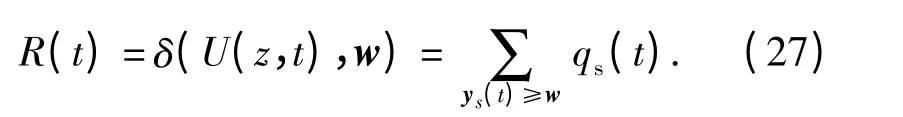
2)系统结构函数未知

如果系统结构函数未知，在得到分系统的向量通用生成函数之后，不能直接利用式(15)、式(16)、式(17)得到系统的向量通用生成函数。一般来说，对于串-并联系统，当各分系统都可靠时，系统可靠。因此可以根据各分系统的最小性能需求分别得到各分系统的可靠度，从而得到系统可靠度。

定义wi为分系统i 的最小性能需求，则t 时刻分系统i 的可靠度为

t 时刻系统可靠度为

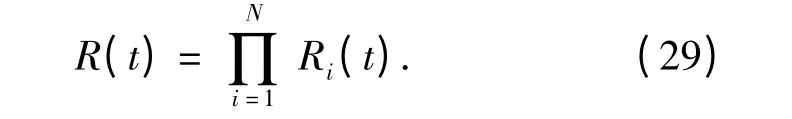
3)系统性能与部分分系统性能有函数关系

如果系统性能与部分分系统性能有明确的函数关系，不失一般性，设前d(d＜N)个分系统的性能与系统性能有明确函数关系，则t 时刻系统可靠度为

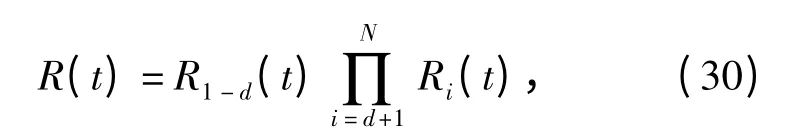
式中，R1-d(t)为前d 个分系统的可靠度，利用式计算;Ri(t)为t 时刻分系统i 的可靠度，利用式计算，i=d+1，…，N.

4 算例分析

性能退化系统在工作时呈现出多种性能状态，是一种比较典型的多态系统。通过性能退化分析可以得到性能退化系统的退化特性，从而得到其性能可靠性［29］。一个由性能退化部件组成的多态系统，如果各部件的性能退化特性已知，利用传统的可靠性分析方法很难得到系统的性能可靠性。从上面的介绍中知道，向量通用生成函数可以描述部件状态性能和对应概率与系统状态性能和对应概率的关系，从而得到系统的性能与可靠性。下面将利用本文的分析方法进行算例分析，以验证其有效性。

如图2所示的串-并联系统由3 个分系统组成，包含6 个性能退化部件。其中，部件1 和2 属于同种类型，部件3、4 和5 属于同种类型。假设6 个性能退化部件的退化特性已经比较了解，部件退化性能、分系统结构函数和系统结构函数见表1。系统的最小性能需求为w=(10.0，4.5).

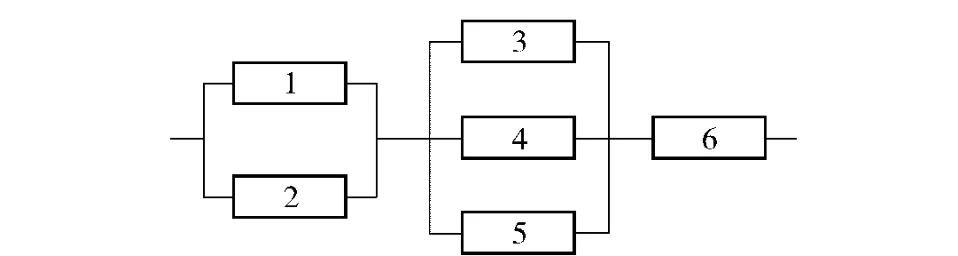
图2 多台串-并联系统Fig.2 An example of multi-state series-parallel system

从表1可以看出，如果定义G6(t)≥7.0 时部件6 正常，则系统性能可以根据分系统1 和2 的性能得到，而分系统3(即部件6)的性能与系统性能没有明确的函数关系，因此，在采用向量通用生成函数进行分析时，可以采用式进行计算，其中，d=2.

当t=10 000 h 时，如果采用Monte Carlo 仿真方法进行分析，则系统的可靠度约为0.812 7.下面的分析中，以Monte Carlo 仿真方法所得到的结果为参考值。

表1 部件退化性能及分系统结构函数、系统结构函数Tab.1 Performance of degraded components andstructure functions of subsystems and the system

如果采用传统可靠性分析方法，每个部件只有两个状态，对于部件1 和2，当部件性能不小于(5.0，4.5)时，部件1 和2 正常，分系统1 正常。对于部件3、4 和5，当部件性能不小于(3.4，4.5)时，部件3、4 和5 正常，分系统2 正常。对于部件6，当部件性能不小于7.0 时，部件6 正常，分系统3 正常。此时，采用传统可靠性分析方法可以得到系统可靠度为0.470 5.

根据上面定义的2 个状态，采用向量通用生成函数进行分析，得系统可靠度为0.470 5;如果每个部件定义4 个状态，则系统可靠度为0.784 5;如果每个部件定义16 个状态，则系统可靠度为0.789 2.部件状态数与系统可靠度的对应情况见表2.

可以看出，随着部件状态数的增加，采用本文方法所得到的估算结果越来越与Monte Carlo 仿真得到的参考值接近。当部件状态数大于256 时，系统可靠度稳定在0.812 6.随着部件状态数的增加，所得到的估算结果越来越准确，但是计算量越来越大。

表2 部件状态数与系统可靠度Tab.2 Number of component states and system reliability

当部件状态数为256 时，如果不合并同类项，分系统1 有2562个状态，分系统2 有2563个状态，系统有2565个状态，计算量太大而难以计算。合并同类项之后，分系统1 有688 个状态，分系统2 有2 032个状态，系统有3 750 个状态，系统的可靠度为0.812 6，计算时间为7.5 s.如果采用状态重新划分法将分系统性能重新划分为64 个状态，则系统的可靠度为0.812 3，计算时间为4.7 s.可以看出，通过合并同类项和状态重新划分法，能够极大地提高计算效率，特别是当部件数较多时，效果会更加明显。

分别采用传统可靠性分析方法、Monte Carlo 仿真方法和本文方法，分析时间与系统可靠度关系，如图3所示。

从图3可以看出，传统可靠性分析方法在分析具有多种性能水平的多态系统可靠性时，所估算的可靠度与Monte Carlo 仿真方法所得到的结果相比十分保守，而本文方法与Monte Carlo 仿真方法所得结果粘合在一起，基本完全相同。

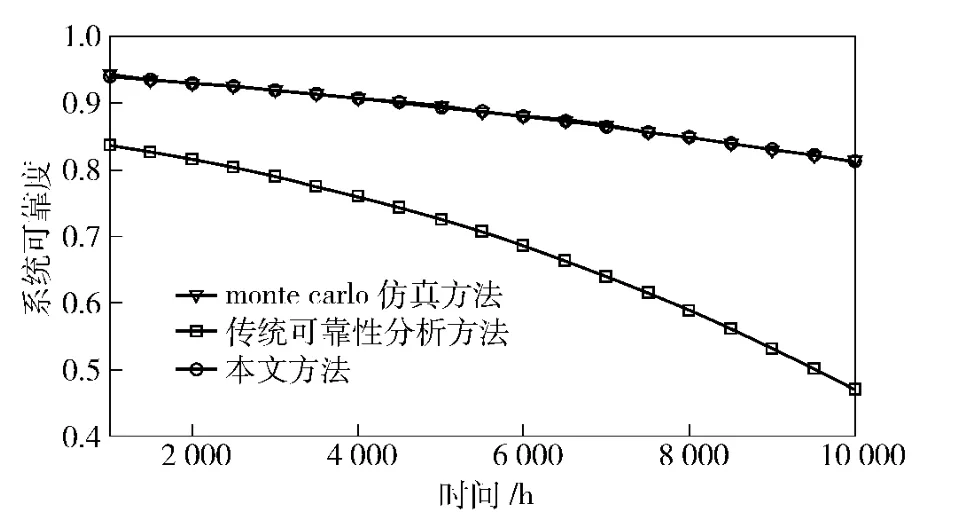
图3 3 种方法得到的时间与系统可靠度关系Fig.3 The relationship between system reliability and time obtained by the three methods

5 结论

1)提出了向量通用生成函数的定义和对应的运算方法，并且利用向量通用生成函数分析了多性能参数多态系统的可靠性问题。

2)向量通用生成函数能够快速地估算多性能参数多态系统的可靠度，与Monte Carlo 仿真方法的结果对比显示，其所得到的结果准确可信。

3)利用向量通用生成函数估算可靠度时，其估算的精度与状态数有关。对于性能退化系统，状态划分时定义的状态数越多，计算精度越高，但计算越复杂。采用合并同类项和状态重新划分法可以有效减少计算量。

4)多态系统可靠性考虑了部件性能与系统性能的关系，性能与可靠度的关系，从而可以利用性能进行可靠性分析与优化设计，这为可靠性设计的发展提供了新的思路，能够有效避免目前工程中性能设计与可靠性设计相脱离的情况。

References)

［1］Levitin G.The universal generating function in reliability analysis and optimization［M］.London:Springer，2005.

［2］Lisnianski A，Levitin G.Multi-state system reliability:Assessment，optimization and applications［M］.Singapore:World Scientific，2003.

［3］Huang J S，Zuo M J.Dominant multi-state systems［J］.IEEE Transactions on Reliability，2004，53(3):362 -368.

［4］Barton R M，Damon W W.Reliability in a multi-state system［C］∥Proceedings of the Sixth Annual Southeastern Symposium on Systems Theory.Louisiana:1974.

［5］Barlow R E，Wu A S.Coherent systems with multi-state components［J］.Mathematics of Operations Research，1978，3:275 -281.

［6］Massim Y，Zeblah A，Meziane R，et al.Optimal design and reliability evaluation of multi-state series-parallel power systems［J］.Nonlinear Dynamics，2005，40:309 -321.

［7］Taboada H A，Espiritu J F，Coit D W.Design allocation of multistate series-parallel systems for power systems planning:a multiple objective evolutionary approach［J］.Journal of Risk and Reliability，2008，222(3):381 -391.

［8］Yeh W C.A simple universal generating function method for estimating the reliability of general multi-state node networks［J］.IIE Transactions，2009，41:3 -11.

［9］Jane C C，Laih Y W.A practical algorithm for computing multistate two-terminal reliability［J］.IEEE Transactions on Reliability，2008，57(2):295 -302.

［10］Krzysztof K，Joanna S.On multi-state safety analysis in shipping［J］.International Journal of Reliability，Quality and Safety Engineering，2007，14(6):547 -567.

［11］Kolowrocki K，Kwiatuszewska-sarnecka B.Reliability and risk analysis of large systems with ageing components［J］.Reliability Engineering and System Safety，2008，93:1821 -1829.

［12］宋月，刘三阳，冯海林.相邻k-out-of-n :F 多状态可修系统的可靠性分析［J］.系统工程与电子技术，2006，28(2):310-316.SONG Yue，LIU San-yang，FENG Hai-lin.Reliability analysis of consecutive k-out-of-n :F repairable systems with multi-state component［J］.Systems Engineering and Electronics，2006，28(2):310 -316.(in Chinese)

［13］武月琴，周泓，官建成.一类多状态系统的可靠性计算［J］.北京航空航天大学学报，2007，33(8):968 -971.WU Yue-qin，ZHOU Hong，GUAN Jian-cheng.Reliability estimation of a multi-state system［J］.Journal of Beijing University of Aeronautics and astronautics，2007，33(8):968 -971.(in Chinese)

［14］原菊梅，侯朝桢，高琳，等.粗糙Petri 网及其在多状态系统可靠性估计中的应用［J］.兵工学报，2007，28(11):1373 -1376.YUAN Ju-mei，HOU Chao-zhen，GAO Lin，et al.Rough Petri net and its application in multi-state system reliability estimate［J］.Acta Armamentarii，2007，28(11):1373 - 1376.(in Chinese)

［15］周金宇，谢里阳，王学敏.多状态系统共因失效分析及可靠性模型［J］.机械工程学报，2005，41(6):66 -70.ZHOU Jin-yu，XIE Li-yang，WANG Xue-min.Analysis for common cause failure and reliability model in multi-state systems［J］.Chinese Journal of Mechanical Engineering，2005，41(6):66-70.(in Chinese)

［16］Li Chun-yang，Chen Xun，Yi Xiao-shan.Redundancy optimization for multi-state system in the presence of common cause failures［C］∥The 2008 International Conference on Risk and Reliability Management.Beijing:2008:632 -636.

［17］Li Chun-yang，Chen Xun，Yi Xiao-shan，et al.Heterogeneous redundancy optimization for multi-state series-parallel systems subject to common cause failures［J］.Reliability Engineering and System Safety，2010，95(3):202 -207.

［18］Zaitseva E，Levashenko V.Investigation multi-state system reliability by structure function［C］∥Proceedings of the 2nd International Conference on Dependability of Computer Systems.Poland，2007:81 -90.

［19］Ramirez-marquez J E，Coit D W.A Monte-Carlo simulation approach for approximating multi-state two-terminal reliability［J］.Reliability Engineering and System Safety，2005，87:253 -264.

［20］Zio E，Marella M，Podofillini L.A Monte Carlo simulation approach to the availability assessment of multi-state systems with operational dependencies［J］.Reliability Engineering and System Safety，2007，92:871 -882.

［21］Taboada H A，Espiritu J F，Coit D W.MOMS-GA:a multi-objective multi-state genetic algorithm for system reliability optimization design problems［J］.IEEE Transactions on Reliability，2008，57(1):182 -191.

［22］Ushakov I.Universal generating function［J］.Soviet Journal of Computer and Systems Sciences，1986，24(5):118 -129.

［23］Ushakov I.Optimal standby problems and a universal generating function［J］.Soviet Journal of Computer and Systems Sciences，1987，25(4):79 -82.

［24］Levitin G.A universal generating function approach for the analysis of multi-state systems with dependent elements［J］.Reliability Engineering and System Safety，2004，84(3):285 -292.

［25］Ouzineb M，Nourelfath M，Gendreau M.Tabu search for the redundancy allocation problem of homogenous series-parallel multistate systems［J］.Reliability Engineering and System Safety，2008，93(8):1257 -1272.

［26］Tian Z G，Levitin G，Zuo M J.A joint reliability redundancy optimization approach for multi-state series– parallel systems［J］.Reliability Engineering and System Safety，2009.

［27］An Z W，Huang H Z，Liu Y.A discrete stress-strength interference model based on universal generating function［J］.Reliability Engineering and System Safety，2008，93(10):1485 -1490.

［28］An Z W，Huang H Z，Lin D.An approach to reliability evaluation of multiple V-belt drives considering the deviation of belt length［J］.Journal of Risk and Reliability，2009，223(2):159-166.

［29］Wang P，Coit D W.Reliability prediction based on degradation modeling for systems with multiple degradation measures［C］∥Proceedings Annual Reliability and Maintainability Symposium.Los Angeles，2004:302 -307.