一类非完整链式系统的有限时间镇定控制
2010-02-21王轶卿李胜陈庆伟
王轶卿,李胜,陈庆伟
(南京理工大学 自动化学院,江苏 南京210094)
0 引言
近年来,随着自动控制技术的发展和人们对控制系统稳定性、快速性、准确性要求的不断提高,有限时间控制成为控制理论界研究的前沿课题之一。由于系统在有限时间控制律的作用下具有收敛速度快、稳态精度高、鲁棒性好的优点,有限时间控制问题自问世以来受到了各国学者的广泛关注。针对该问题目前人们提出的主要方法有:齐次系统方法[1-3]、有限时间Lyapunov 函数法[4-5]、终端滑模控制法[6-8]等,其中一些已成功地应用于一些实际对象的控制,如非完整移动机器人的控制[9]。但从目前的研究成果来看,非完整系统的有限时间镇定控制还存在一些问题,如所提控制器存在奇异性、不连续等问题[9-10],这主要是由于非完整系统自身的一些特性和控制器设计方法所造成的。
自非完整系统镇定控制问题被提出以来,人们就试图寻找一种反馈控制律,使得以非完整系统为对象的闭环系统在平衡点渐近稳定或指数稳定,但由于非完整系统不满足Brockett 定理[11]中提出的非线性系统在平衡点附近存在连续可微反馈镇定控制器的必要条件,所以理论上不存在光滑的、时不变状态反馈控制器,使非完整系统在平衡点稳定或渐近稳定。针对这一问题,众多学者分别提出了非连续时不变镇定控制器[12-14]、连续时变镇定控制器[15]、混杂控制器[16]三类控制器解决非完整系统的反馈镇定问题。其中非连续时不变镇定控制器只能实现非全局情况下,系统各状态指数稳定。连续时变镇定控制器虽然可以实现系统的全局指数稳定,但在反馈控制器中需要引入时间变量。混杂控制器则根据预先设定的时间序列在连续时不变控制器间切换,使得非完整系统各状态指数收敛。从所得结论可以看出,上述控制器虽然可以实现系统的指数稳定,但各状态均不能在有限时间内收敛到平衡位置。尤其是当各状态与平衡点之间偏差较小时,系统过渡时间较长。
本文针对一类三维非完整链式系统,提出了2种基于切换控制策略的有限时间镇定控制器,并分别应用齐次系统方法和终端滑模控制理论,证明了在所设计的有限时间镇定控制器的作用下,系统各状态能在有限时间内从任意的非平衡位置收敛至平衡点。与一些已有非完整系统有限时间镇定控制器相比,本文提出的2 种控制器均具有非奇异的特点。
1 问题描述
本文主要研究了非完整链式系统

的有限时间镇定问题,即设计反馈控制器

使得三维链式系统中3 个状态x1,x2,x3,能够在有限时间内收敛至平衡位置。其中:[x1,x2,x3]为三维非完整系统的状态向量;[u1,u2]为系统输入向量;实际中很多非完整系统可以通过适当的坐标变换转换成此类系统,如2 轮驱动的移动机器人、滚动的圆盘、独轮小车等系统。
定义1 非线性系统
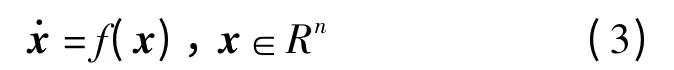
是有限时间稳定的是指系统满足Lyapunov 稳定性,且可在有限时间内收敛至平衡点[2]。其中:f(x)为连续的向量函数。
2 有限时间镇定控制器设计
2.1 基于齐次系统的有限时间控制器设计
在设计系统(1)的有限时间控制器之前,我们先给出一些相关的引理:
引理1[2]对Brunovsky 标准型的线性系统:

控制器:

可以在有限时间内将其各状态镇定至平衡位置。其中:ki>0,且使得多项式:

为Hurwitz 多项式;αi(i=1,2,…,n)之间满足:
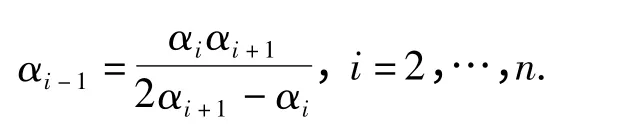
并且αn+1=1,αn=α,0<α<1;sign(x)表示符号函数,即:

在上述定义和引理的基础上,本文得到了如下定理。
定理1 非完整链式系统(1)在切换控制器
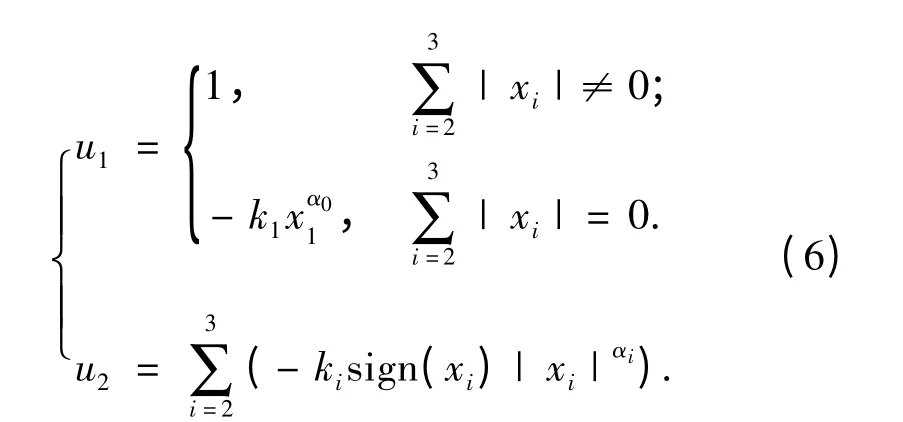
的作用下是有限时间稳定的。其中:ki>0,i =1,2,3,且使得多项式
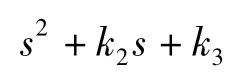
为Hurwitz 多项式;α0=p/q,p,q 为正奇数且p<q,α2,α3之间满足:

证明:首先由三维非完整链式系统(1)可知:
当u1(x)=1 时,系统的部分状态可表示为Brunovsky 标准型的线性系统:

其中:z1=x3,z2=x2,v =u2;由引理1 可知,系统(7)在控制器
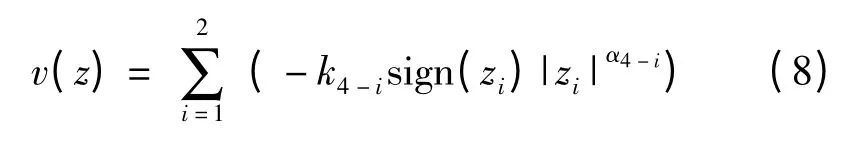
作用下是有限时间稳定的。其中:k2>0,k3>0,且使得多项式:
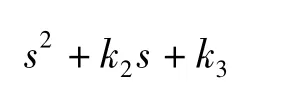
为Hurwitz 多项式; α2,α3之间满足:

并且α1=1,α2=α,0<α<1.
将z1=x3,z2=x2,v =u2代入控制器(8),可知,系统(1)在控制器
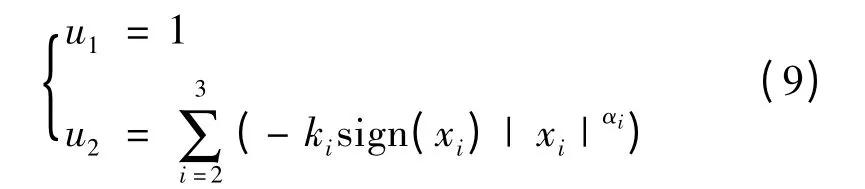
的作用下,状态x2,x3能在有限时间[0,t1]内从非平衡位置收敛至平衡位置x2=0,x3=0,并且由x·1=1可知,状态x1在这段时间内的变化有界,从初始值x10变化到(x10+t1).
而当状态x2,x3在t1时刻到达平衡位置后,由于x2=0,x3=0,因此u2=0,x2u1=0,故控制输入u1从u1=1 切换至u1=-k1xα01后,系统状态x2,x3可以保持在平衡位置不变,而求解微分方程x·1=-k1xα01,可得状态x1关于时间的方程:
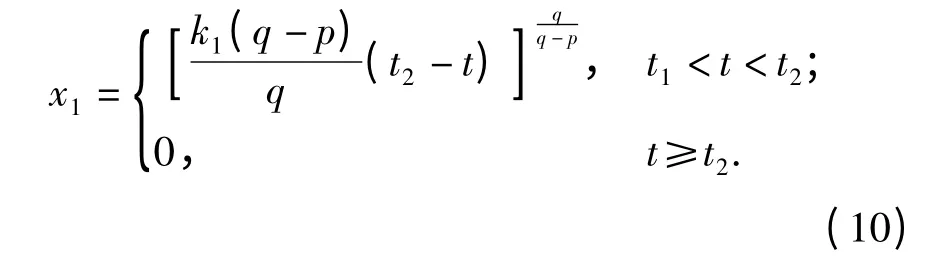
由此可知状态x1可以在有限时间段(t1,t2]内从(x10+t1)收敛至平衡位置x1=0,并且:

因此,3 维非完整链式系统(1)在切换控制器(6)的作用下是有限时间稳定的。定理得证。
2.2 基于终端滑模的有限时间控制器设计
定理2 非完整链式系统(1)在控制器

的作用下是有限时间稳定的。其中,k >0;γ=n0/m0,n0,m0为互质的正奇数且n0<m0;β >0;p =m/n,m,n 为互质的正奇数且n<m<2n;λ >0;q =n1/m1,m1,n1为互质的正奇数且n1<m1.
证明:当u1(x)=1 时,系统的状态方程可表示为

其中,子系统

为一个2 阶Brunovsky 标准型的线性系统。
首先证明子系统(14)可以在有限时间内到达滑动平面s:

对所选滑动平面式(15)求导得:

将式(12)中u2和式(14)代入式(16),得:

当p=m/n;m,n 为互质的正奇数且n<m<2n时,xp-12≥0:
1)若xp-12>0,则对于任意x2,总存在ε,使得λpx2p-1>ε >0,因此,子系统(14)可以在有限时间内收敛到滑动平面。
2)若xp-12=0,则x2=0,若此时x3=0,则s=0.若x3≠0,由=u2可推得:

由此可知,系统不会停留在x2=0 且x3≠0 的状态,而当x2≠0 时,xp-12>0,问题可归于1).
因此,子系统(14)在有限时间[0,t1]内到达切换平面。
由式(14)和s =x2p+βx3=0 可得:即求解该微分方程,可得状态x3关于时间的方程:
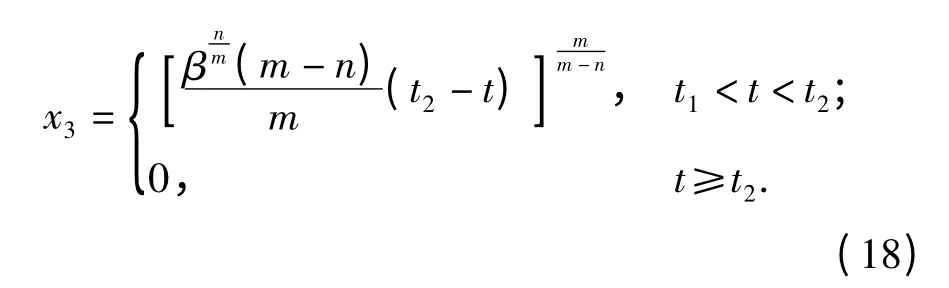
由此可知,子系统(14)各状态在到达滑模面s后,可在有限时间段(t1,t2]内沿滑模面s 收敛至原点,且所需时间为
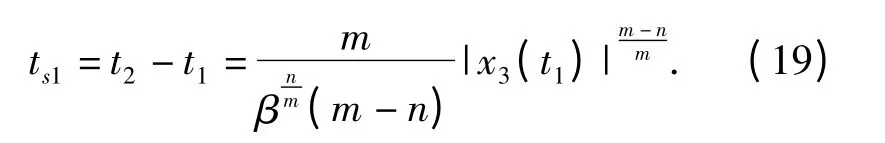
当系统状态x2和x3到达平衡位置后,由于x2=0,x3=0,因此u2=0,x2u1=0,故控制输入u1从u1=1切换至u1=-kxγ1后,系统其余状态x2和x3可以保持在平衡位置不变,而求解微分方程x·1=-kxγ1,可得状态x1关于时间的方程:
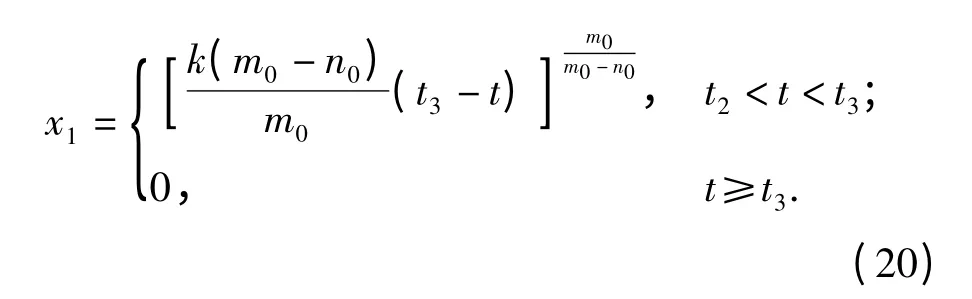
由此可知状态x1可以在有限时间段(t2,t3]内从(x10+t2)收敛至平衡位置x1=0,并且:

综合上述证明可知,非完整链式系统(1)各状态在控制器(12)的作用下在有限时间内收敛至原点。定理得证。
2.3 2 种有限时间控制器比较
从上述2 种有限时间控制器证明过程可知,上述两种控制器均可使系统(1)各状态在有限时间内收敛至平衡位置。但相比于控制器(6),控制器(12)的参数与系统各状态收敛至平衡状态时刻的关系更为清晰,当参数κ、β、λ、m0-n0、m1-n1、m -n 越大时,在控制器(12)的作用下,系统各状态能更快地到达平衡位置,否则系统各状态到达平衡位置的时间较长。
3 仿真
本节各图中,状态x1,x2的单位为red;x3的单位为rad2;控制输入u1、u2的单位为rad/s.
3.1 基于齐次系统的有限时间控制方法
由定理1 可知,3 维非完整链式系统(1)在如下控制器:

的作用下,系统各状态可以在有限时间内收敛至零点。在满足定理1 中参数选择条件下,控制器各参数分别选取为:k1=5,k2=2,k3=1,α0=1/3,α2=3/5,α3=3/7.
当系统各状态初始值分别为:x1(0)=1,x2(0)=2,x3(0)=3 时,在控制器(22)的作用下,系统各状态的变化曲线和控制输入曲线分别如图1和图2所示。
当系统各状态初始值分别为:x1(0)=10,x2(0)=20,x3(0)=30 时,在控制器(22)的作用下,系统各状态的变化曲线和控制输入曲线分别如图3和图4所示。
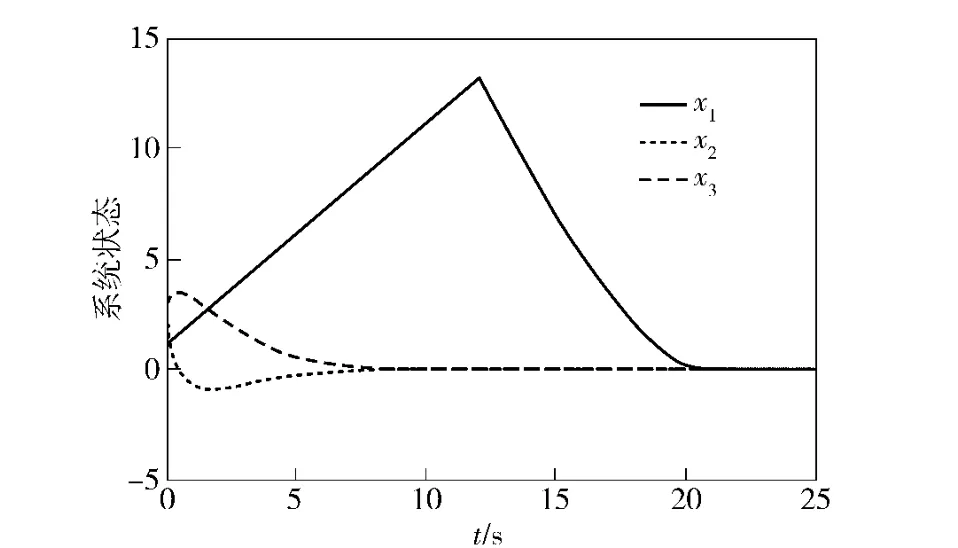
图1 系统(1)在控制器(22)的作用下,各状态的时间响应曲线Fig.1 The curves of states of the system (1)under the controller (22)

图2 系统(1)在控制器(22)的作用下,各控制输入曲线Fig.2 The curves of inputs of the system (1)under the controller (22)

图3 远离平衡状态时,系统(1)在控制器(22)的作用下,各状态的时间响应曲线Fig.3 The curves of states of the system (1)under the controller (22)when the initial states are far away from the equilibrium
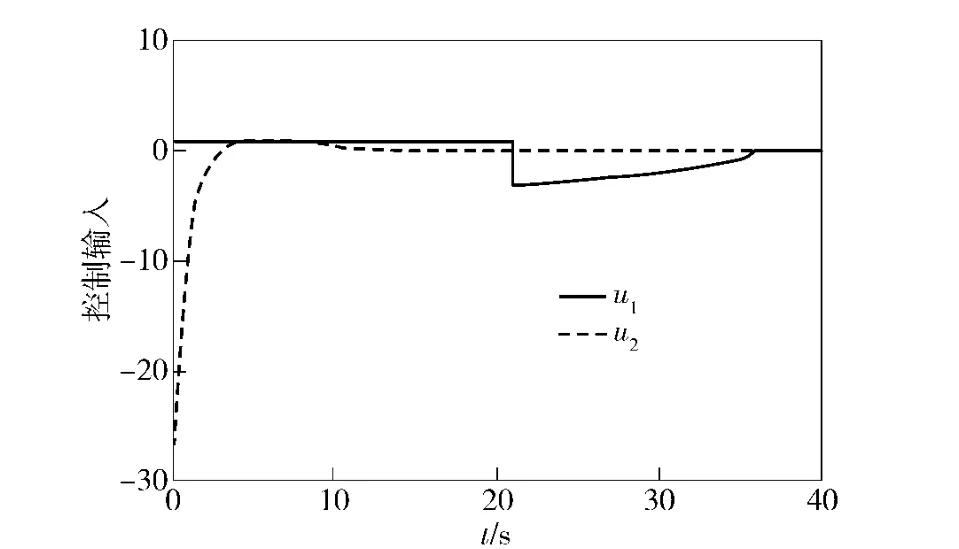
图4 远离平衡状态时,系统(1)在控制器(22)的作用下,各控制输入曲线Fig.4 The curves of inputs of the system (1)under the controller (22)when the initial states are far away from the equilibrium
从图1和图3可以看出,不论三维非完整系统各状态的初始位置是否远离平衡状态,系统(1)均可以在控制器(22)的作用下收敛于平衡状态,但当初始位置远离平衡状态时,各状态到达平衡位置的时间较长,同时从图2和图4可以看出控制器的切换时刻也较晚,主要是由于状态x2、x3的初始位置远离平衡位置所致。
3.2 基于终端滑模的有限时间控制方法
由定理2 可知,3 维非完整链式系统(1)在如下控制器:
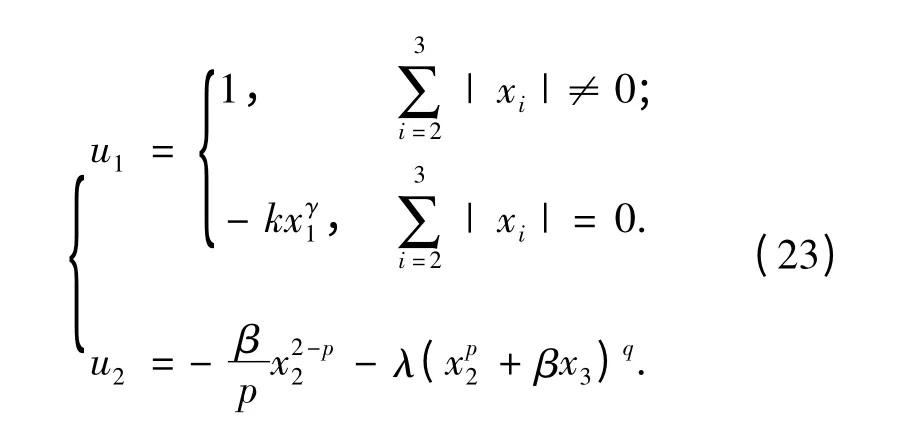
的作用下,系统各状态可以在有限时间内收敛至零点。在满足定理2 中参数选择条件下,控制器各参数分别选取为:k =1,γ =1/3,β =1,λ =1,p =5/3,q=1/3.
当系统各状态初始值分别为:x1(0)=1,x2(0)=2,x3(0)=3 时,在控制器(23)的作用下,系统各状态的变化曲线和控制输入曲线分别如图5和图6所示。
当系统各状态初始值分别为:x1(0)=10,x2(0)=20,x3(0)=30 时,在控制器(23)的作用下,系统各状态的变化曲线和控制输入曲线分别如图7和图8所示。
从图5和图7可以看出,与控制器(22)相似,不论系统(1)各状态的初始位置是否远离平衡状态,该系统均可以在控制器(23)的作用下收敛于平衡状态,但当初始位置远离平衡状态时,各状态到达平衡位置的时间较长,同时从图6和图8可以看出控制器的切换时刻也较晚,主要是由于状态x2、x3的初始位置远离平衡位置所致。

图5 系统(1)在控制器(23)的作用下,各状态的时间响应曲线Fig.5 The curves of states of the system (1)under the controller (23)

图6 系统(1)在控制器(23)的作用下,各控制输入曲线Fig.6 The curves of inputs of the system (1)under the controller (23)
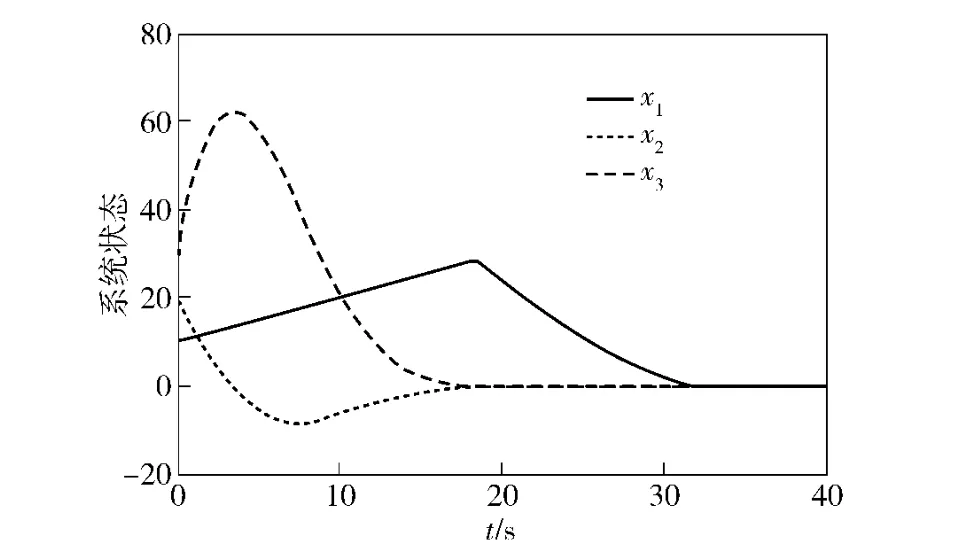
图7 远离平衡状态时,系统(1)在控制器(23)的作用下,各状态的时间响应曲线Fig.7 The curves of states of the system (1)under the controller (23)when the initial states are far away from the equilibrium
综合以上2 种控制方法,可以看出,基于齐次系统方法的有限时间控制器和基于终端滑模方法的有限时间控制器均可以在有限时间内使得三维非完整链式系统(1)的所有状态由任意初始位置收敛至平衡状态。同时,对比图1和图5、图3和图7,可以发现,系统(1)各状态在相同初始位置下,控制器(23)比控制器(22)能够使系统各状态在更短的时间内到达平衡位置,即系统(1)在基于终端滑模方法的有限时间控制器的作用下收敛速度更快一些,且这一优势在系统的初始状态偏离平衡位置较近时尤为明显。从图2、图4、图6和图8可以看出,系统的控制输入均为有界输入,但同时也可以看到,由于本文所提控制器的控制输入采用了切换控制策略,因此在控制过程中控制输入出现了较大幅度的变化,还有待利用无扰动切换技术予以改进。

图8 远离平衡状态时,系统(1)在控制器(23)的作用下,各控制输入曲线Fig.8 The curves of states of the system (1)under the controller (23)when the initial states are far away from the equilibrium
4 结论
本文针对一类三维非完整链式系统的有限时间镇定问题,提出了2 种基于切换控制策略的有限时间控制器,并基于齐次系统方法和终端滑模控制理论进行了证明:当所设计控制器各参数满足给定条件时,在所设计控制策略的作用下,系统各状态可在有限时间内从任意非平衡位置收敛于平衡位置。最后利用仿真示例验证了所设计控制器的有效性,并对两种控制器的性能进行了比较,从仿真结果可以看出,本文所提控制策略均能较好的解决三维非完整链式系统的有限时间镇定问题。
References)
[1]李世华,丁世宏,田玉平.一类二阶非线性系统的有限时间状态反馈镇定方法[J].自动化学报,2007,33(1):101 -103.LI Shi-hua,DING Shi-hong,TIAN Yu-ping.A finite-time state feedback stabilization method for a class of second order nonlinear systems[J].Acta Automatica Sinica.2007,33(1):101 -103.(in Chinese)
[2]Bhat S P,Bernstein D S.Geometric homogeneity with applications to finite-time stability[J].Mathematics of Control,Signals,and Systems,2005,17 (2):101 -127.
[3]Bhat S P,Bernstein D S.Finite-time stability of continuous autonomous systems[J].SIAM Journal of Control and Optimization,2000,38(3):751 -766.
[4]Bhat S P,Bernstein D S.Lyapunov analysis of finite-time differential equations[C]∥Proceeding of American Control Conference Seattle,1995:1831 -1832.
[5]Hong Y G.Finite-time stabilization and stabilizability of a class of nonlinear systems[J].Systems Control Letters,2002,46(2):231 -236.
[6]Hong Y G,Yang G W,Cheng D Z,et al.Finite time convergent control using terminal sliding mode[J].Journal of Control Theory and Applications,2004,(2):69 -74.
[7]Hong Y G,Yang G W,Cheng D Z,et al.A new approach to terminal sliding mode control design[J].Asian Journal of Control,2005,7(2):177 -181.
[8]Feng Y,Yu X H,Man Z H.Nonsingular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38:2159 -2167.
[9]祝晓才,董国华,胡德文.轮式移动机器人有限时间镇定控制器设计[J].国防科技大学学报,2006,28(4):121 -127.ZHU Xiao-cai,DONG Guo-hua,HU De-wen.Finite-time stabilization controller for wheeled mobile robot[J].Journal of National University of Defense Technology,2006,28(4):121 -127.
[10]Jammazi C.Finite-time partial stabilizability of chained systems[J].Comptes Rendus Mathematique,2008,346(17 -18):975-980.
[11]Brockett R W.Asymptotic stability and feedback stabilization[C]∥Differential Geometric Control Theory.Boston,1983:181-191.
[12]Astolfi A.On the stabilization of nonholonomic systems[C]∥Proceedings of the 33rd IEEE Conference on Decision and Control.Lake Buena Vista,1994:3481 -3486.
[13]Tayebi A,Tadjine M,Rachid A.Invariant manifold approach for the stabilization of nonholonomic systems in chained form:application to a car-like mobile robot[C]∥Proceedings of the 36th IEEE Conference on Decision and Control.San Diego,1997:4038 -4043.
[14]Urakubo T.Discontinuous feedback stabilization of a class of nonholonomic systems based on Lyapunov control[C]∥Proceedings of the Fifth International Workshop on Robot Motion and Control.2005:91 -96.
[15]马保离,霍伟.非完整链式系统的时变光滑指数镇定[J].自动化学报,2003,29(2):301 -305.MA Bao-li,HUO Wei.Smooth time-varying exponential stabilization of nonholonomic chained systems[J].Acta Automatica Sinica,2003,29(2):301 -305.(in Chienes)
[16]Isatada Matsune,Guisheng Zhai,Tomoaki Kobayashi,et al.A study on hybrid control of nonholonomic systems [C]∥2005 SICE Annual Conference.Sapporo,2005:211 -214.
