基于偏最小二乘法的两栖突击车风扇泵故障分析

董玉才，何国良，易良海，鞠桂玲，王素云

（装甲兵工程学院，1.非线性科学研究所；2.科研部研究所，北京100072）

液压技术具有功率大、响应快、精度高等特点，随着科学技术的发展，已广泛应用于工业、工程机械、航空航天、舰船、军事等领域的设备中，并成为设备中不可缺少的重要组成部分。目前，液压系统在装甲新装备中应用越来越广，对整车性能的影响也越来越大，尤其是大量应用液压技术的新型装备，液压系统往往处于动力传输的核心地位[1]。与电气、机械系统相比，装甲装备液压系统存在着故障率高、故障检测定位困难等问题，这些问题已成为影响武器装备战斗力发挥的重要因素之一[2]。液压系统故障诊断技术，是随着液压设备不断高度自动化以及对液压系统工作可靠性要求越来越高而发展起来的，是建立在液压控制理论、信息理论和电子技术、传感器技术、人工智能技术等基础上的一门综合性新技术，前人做了大量研究工作[3~11]。某两栖突击车的风扇泵为柱塞式，随着使用时间的增加，柱塞与柱塞孔和缸体端面与配油盘两摩擦副的磨损间隙，会逐渐增大，导致油液泄漏增加，容积率下降[2]，当泄漏量达到允许的极限值时，就要进行更换或者大修。

偏最小二乘回归，是一种新的多元数据分析方法，1983年由S.Wold和C.Albano等人首次提出。其集多元线性回归、典型相关分析和主成分分析的基本功能为一体，将建模预测类型的数据分析方法，与非模型式的数据认识方法有机地结合起来。因此，偏最小二乘回归较传统的回归分析、主成分分析具有更大优势，从而使模型精度、稳健性、实用性得到提高[13]。本文研究影响两栖突击车风扇泵泄漏量的相关因素，利用偏最小二乘回归方法的模型对泄漏量进行的预测，为维修人员掌握元件的性能变化趋势，提供科学合理的决策依据。

1 偏最小二乘回归模型

1.1 建模原理

在第一个成分t1和u1被提取后，分别实施X对t1的回归以及Y对u1的回归。如果回归方程已经达到满意的精度，则算法终止；否则，将利用X被t1解释后的残余信息以及Y被t1解释后的残余信息进行第二轮的成分提取。如此往复，直到能达到一个较满意的精度为止。若最终对X共提取了m个成分t1，…，tm，偏最小二乘回归将通过实施yk对t1，…，tm的回归，然后再表达成yk关于原变量x1，…，xm的回归方程（k=1，2，…，q）。

1.2 交叉有效性检验

在偏最小二乘回归建模中，究竟应该选取多少个成分为宜，可通过考察增加一个新的成分后，能否对模型的预测功能有明显的改进来考虑。采用类似于抽样测试法的工作方式，把所有n个样本点分成两部分：第一部分除去某个样本点i的所有样本点集合(共含n-1个样本点)，用这部分样本点并使用h个成分拟合一个回归方程；第二部分是把刚才被排除的样本点i代入前面拟合的回归方程，得到yj在样本点i上的拟合值hj（-i）。对于每一个i=1，2，…，n，重复上述测试，则可以定义yj的预测误差平方和为PRESShj。

定义Y的预测误差平方和为PRESSh，有

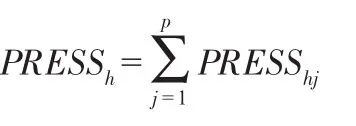
显然，如果回归方程的稳健性不好，误差就很大，它对样本点的变动就会十分敏感，这种扰动误差的作用，就会加大PRESSh的值。

1.3 精度分析

在偏最小二乘回归计算过程中，所提取的自变量成分th一方面可以尽可能多地代表X的变异信息，另一方面又尽可能与Y相关联，解释Y中的信息，定义th的各种解释能力，其中r（xi，xj）表示两个变量之间的相关关系。

成分 t1，t2，…，th对自变量 Xj的累计解释能力

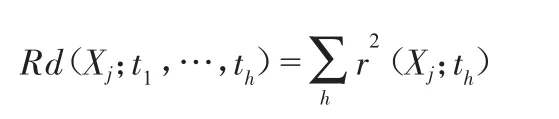
对自变量X的累计解释能力

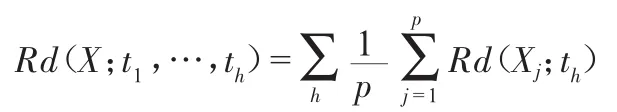
对自变量Y的累计解释能力

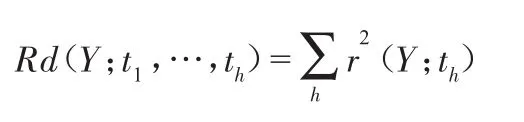
2 试验结果及分析

2.1 试验结果

实车试验以14台不同摩托小时且未换油的某两栖突击车为对象，测得风扇水温、冷却水温以及风扇泵泄露量，结果如表1[2]。风扇泵实时泄漏量极限标准评估模型为[2]

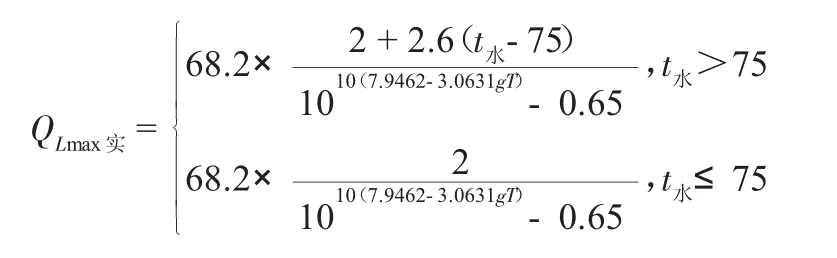
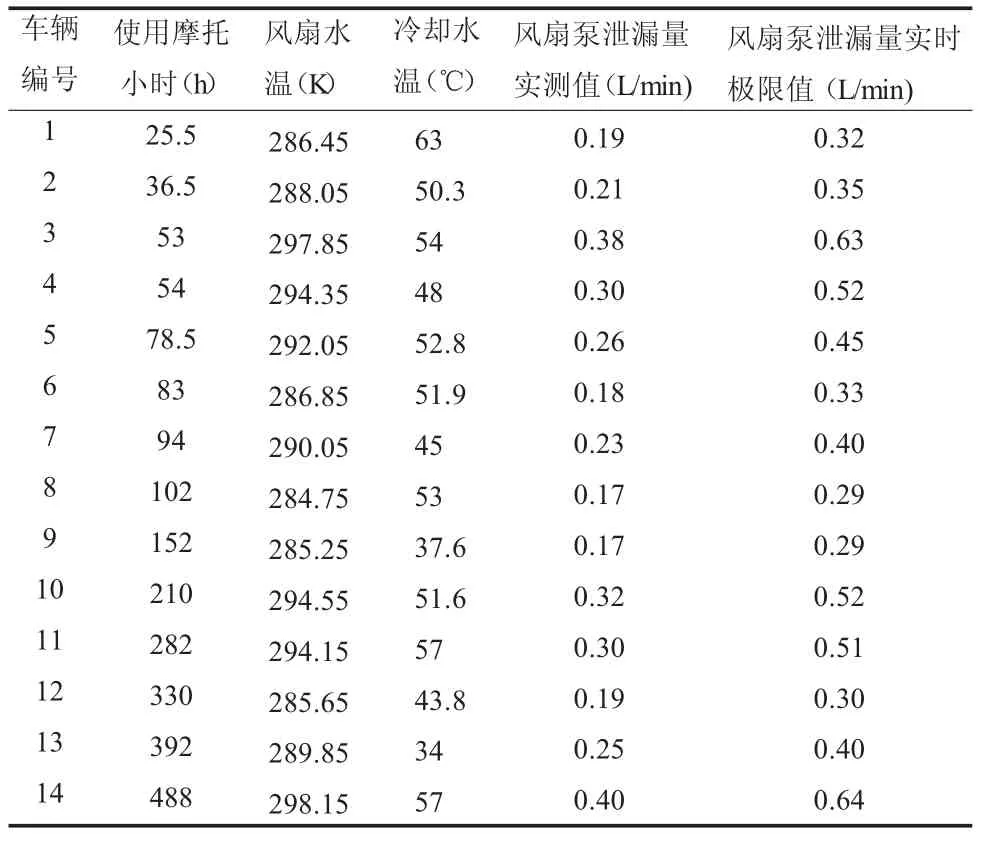
表1 实车测试各因素指标与评估模型实时极限值

记使用摩托小时为x1，风扇水温为x2，冷却水温为x3，风扇泵泄露量实测值为y，考察因变量y与自变量x1，x2，x3的关系。

2.2 偏最小二乘回归模型

经交叉有效性检验，PRESSh= [0.010910.00272 0.00274]，因此h=2时，PRESSh达到最小，模型的预测能力最好，因此取2个主成分t1，t2建立模型，得到风扇泵泄露量的偏最小二乘回归标准化变量模型

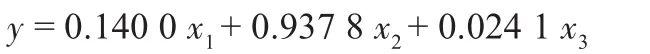
转化为原始变量回归方程为

2.3 模型评价

（1）累计解释能力分析。成分t1，t2，…，th对自变量Y的累计解释能力为。当取 1 个主成分时，t1对y的解释能力为93.97%，当取2个主成分时，t1，t2对y的累计解释能力达到98%以上，能很好地解释了因变量。

（2）偏最小二乘回归成分。图1给出了t1、t2与u1的平面图。从图中可以看出，t1与u1存在明显的线性关系，t2与u1也存在着一定的线性关系，但相对较弱。

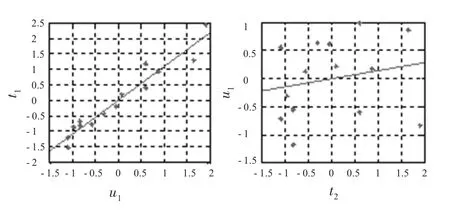
图1 t1/u1、t2/u1平面图

（3）风扇泵泄露量拟合结果。风扇泵泄漏量的实测值与拟合值的对比情况如表2所示。从表中可以看出，最大相对误差不超过7%。风扇泵泄漏量实测值与拟合值对比图如图2所示。

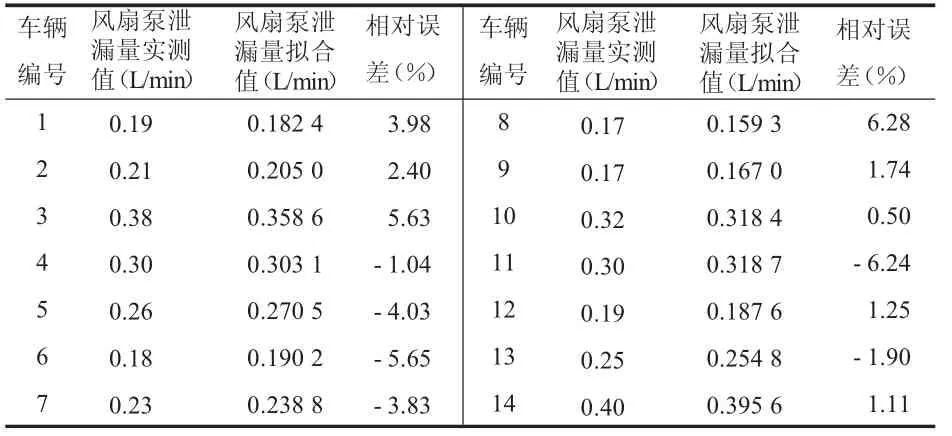
表2 风扇泵泄露量的实测值与拟合值对比结果

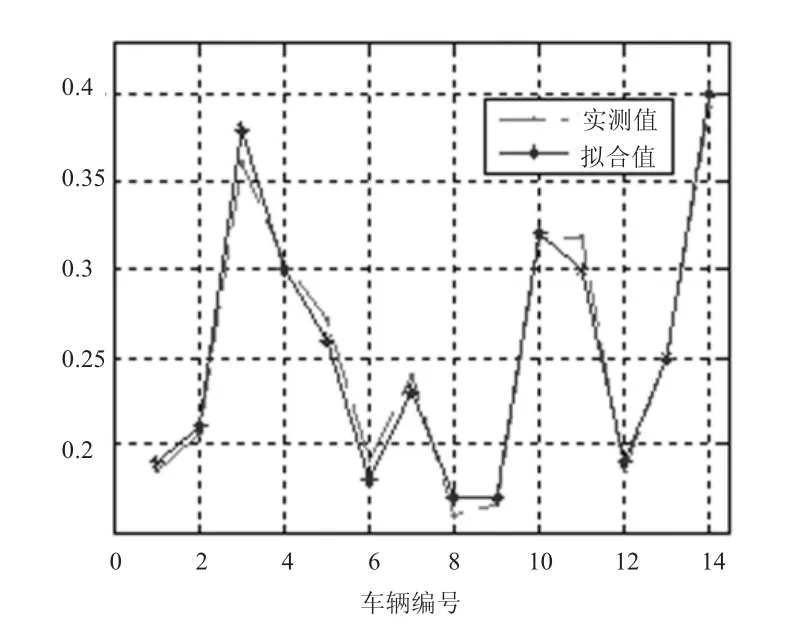
图2 风扇泵泄露量实测值与拟合值对比图

2.4 风扇泵大修期预测

根据偏最小二乘回归模型，在风扇油温为313.15 K、冷却水温为75℃条件下，当使用摩托小时为10 047 h时，将超过风扇泵允许的泄漏量极限1.363 0 L/min。因此，可预测马达的更换期或大修期为10 050 h左右。在实际使用中，还要充分考虑各种环境条件的影响，更换期或大修期应小于预测值，以确保风扇泵的正常运转。

3 结束语

液压设备往往是结构复杂而且是高精度的机、电、液一体化的综合系统，液压泵是液压系统的重要输出执行元件之一，是将原动机输出的机械能转换成液体压力的一种能量转换装置。本文利用偏最小二乘回归方法，经交叉有效性检验，建立了风扇泵泄露量的偏最小二乘回归模型，经分析，主成分对自变量和因变量的累计解释能力较高，模型的拟合值与实测值相对误差较小，并利用该模型对风扇泵泄漏量进行了预测，对于确定合理的风扇泵更换期或大修期具有重要意义。

[1]晁智强，韩寿松，江鹏程.某两栖装甲装备液压系统不解体状态检测与故障诊断[J].中国工程机械学报，2008，(3)：359-369.

[2]盛 锋，程卫红，晁智强，等.某两栖装甲装备液压系统非介入式原位检测方法[J].装甲兵工程学院学报，2009，23(4)：40-44.

[3]刘泽华，陆 清，谷立臣.基于包络-灰色理论的液压系统故障诊断方法研究[J].液压与气动，2008，(1)：77-80.

[4]赵亮培.基于故障数分析的液压系统故障诊断研究[J].液压气动与密封，2008，(6)：19-20.

[5]贺湘宇，何清华，郭 勇，等.基于主元回归模型的挖掘机液压系统故障诊断[J].江苏大学学报，2008，(3)：106-110.

[6]周汝胜，焦宗夏，王少萍，等.基于专家系统的导弹发射车液压系统故障诊断[J].航空学报，2008，29(1)：197-203.

[7]潘 伟，王汉功.基于多传感器信息融合的工程机械液压系统在线状态检测与故障诊断[J].工程机械，2004，(7)：42-45.

[8]虞军胜.轧机液压AGC系统故障智能诊断的研究[D].武汉：武汉科技大学，2006.

[9]姜万录，张焰明，王海军.基于Lyapunov指数分析的液压泵故障诊断方法研究[J].液压与机床，2008，(3)：183-184.

[10]刘泽华.基于小波理论的液压系统诊断特征提取与故障分类方法研究[D].西安：西安建筑科技大学，2007.

[11]潘 兵，熊静琪.多传感器信息融合在液压系统智能诊断中的应用[J].机床与液压，2006，(5)：190-192.

[12]晁智强，刘相波，孟爱红.装甲车辆液压传动[M].北京：兵器工业出版社，2005.

[13]王惠文.偏最小二乘回归方法及其应用[M].北京：国防工业出版社，1999.