燃气负荷组合预测中贝叶斯权重法的应用

陈 贝,臧子璇

(重庆大学城市建设与环境工程学院,重庆400045)

在燃气的中、长期负荷预测中,数据记录不完善、统计信息缺失等是影响预测精度的重要因素,而灰色系统理论正是针对此类“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统的研究,它通过对“部分”已知信息的生成、开发实现对现实的确切描述和认识[1-2]。灰色模型仅利用已知负荷数据达到对未来负荷的预测,但事实上,燃气的年度负荷受到多种因素的影响,如国民经济发展情况、产业结构调整、能源政策、人口和燃气价格等[3]。因此,在利用历史负荷值探寻负荷发展规律的同时考虑其他因素的影响更符合人类对事物发展的认知规律。研究表明,年度负荷与影响因素间具有较高的线性相关性,而各种可以量化的因素之间存在着严重的多重相关性,采用传统的回归分析方法会产生比较大的偏差,而偏最小二乘回归分析方法对此类情况有出色的解决能力。在进行预测模型的组合时,建立基于贝叶斯理论的动态权重模型可保证模型的有效精度。本文采用基于GM(1,1)模型和偏最小二乘回归的贝叶斯组合模型对某市燃气负荷进行了预测。

1 预测方法介绍

1.1 贝叶斯理论

贝叶斯理论的核心是当不能准确知悉一个事物的本质时,可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。用数学语言表达就是：支持某项属性的事件发生得愈多,则该属性成立的可能性就愈大。本文的负荷预测正是基于这种不确定性及可能性思想的理论。在预测领域,Bates等人于1969年首先提出组合预测方法[4]。贝叶斯权重法是根据前期的预测表现,应用贝叶斯组合定理计算出来的条件概率,即模型的信用值。信用值越大,表示这一模型此前的预测表现越好,它就将在下一期的预测中担当主要角色,从而使模型在整个预测区间内始终保持良好的预测精度[5]。

1.2 GM(1,1)模型原理[1-2]

累加生成能够弱化数列随机性,将任意非负的数列、摆动的与非摆动数列转化成为非减的、递增的数列,增强数列的规律性。

将原始数列{x(0)}中的数据x(0)(k)进行一次累加生成处理,则原始数列

记为数列x(1)：

模型的其一阶微分方程形式为：

其中,a,u—模型参数。

将⑷式进行离散化处理得到：

记

得

由最小二乘法解方程组⑺,得到模型参数：

得到离散化微分方程的解为：

累减还原即为GM(1,1)模型的时间相应函数：

2 新型预测方法介绍

2.1 偏最小二乘回归法[6]

偏最小二乘法是一种多自变量对多因变量的建模回归方法,集多元线性回归分析、典型相关分析和主成分分析等功能为一体。它可以解决样本数据较少及变量集合内部存在较高程度的相关性的问题。

数据的标准化处理：

xi—自变量;

Sxi—自变量的均方差;

y＊—因变量的标准化向量;

y—因变量;

Sy—因变量的均方差。

经主成分提取得标准化变量的回归方程：

其中,yˆ＊—标准化自变量的拟合值;αi—标准化方程的系数

由式(12)、(13)得还原为原始变量的回归方程：

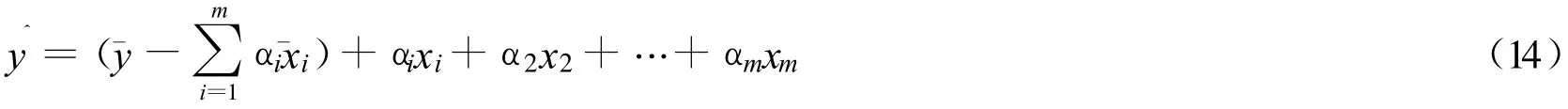
2.2 组合模型[7-8]

将某一特定燃气负荷时间序列表示为函数：

其中,yt—时间序列在时段t的实际值;

式(15)在某一预测时刻只对k个时间序列中的某一值成立或接近,通常这个k值无法事先获知。根据k值的随机性与不确定性的特点,引入一个变量Z表示k的不确定性,Z可以取k中任何值,则可定义条件概率为=Prob(Z=k/yt,yt-1,…,y)。

根据贝叶斯定理可知：

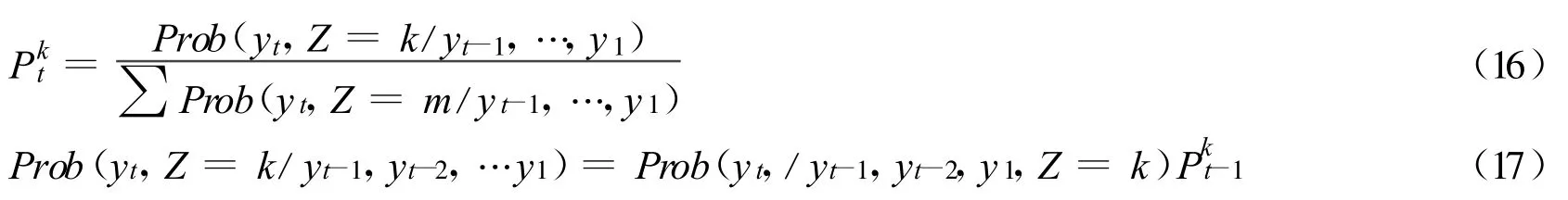
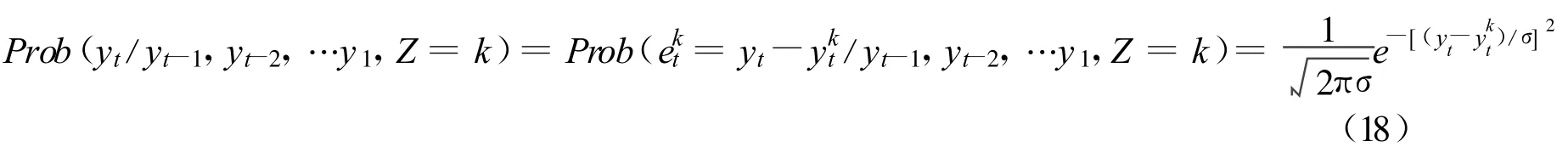
合并得：

式(19)得到的是由模型k产生实际时间序列的概率,称为模型的信用值,即被用做模型k在当前T时间组合预测模型中所拥有的权重,这一权重也将应用于下一时间的组合模型中。可以看出：该模型是一种自适应和启发式算法,能够根据前期实际值及预测误差自动调整各模型的权重,保证预测精度。第t+1时间的预测结果为：

2.3 实例应用

文中选取国内生产总值(x1,亿元)、第二产业产值(x2,亿元);第三产业产值(x3,亿元)、人均国内生产总值(x4,万元)和城市非农业人口数(x5,万人)等5个影响因素对城市燃气年度负荷(y,亿m3)进行偏最小二乘回归分析建模[7]。

表1 某市燃气负荷及各项因素的原始数据

由表1数据得灰色GM(1,1)模型方程：

及偏最小二乘回归模型方程：

由式(19)-(22)即可得出组合模型。拟合结果见表2,实测数据与拟合值的比较,相对误差比较见图1、图2。

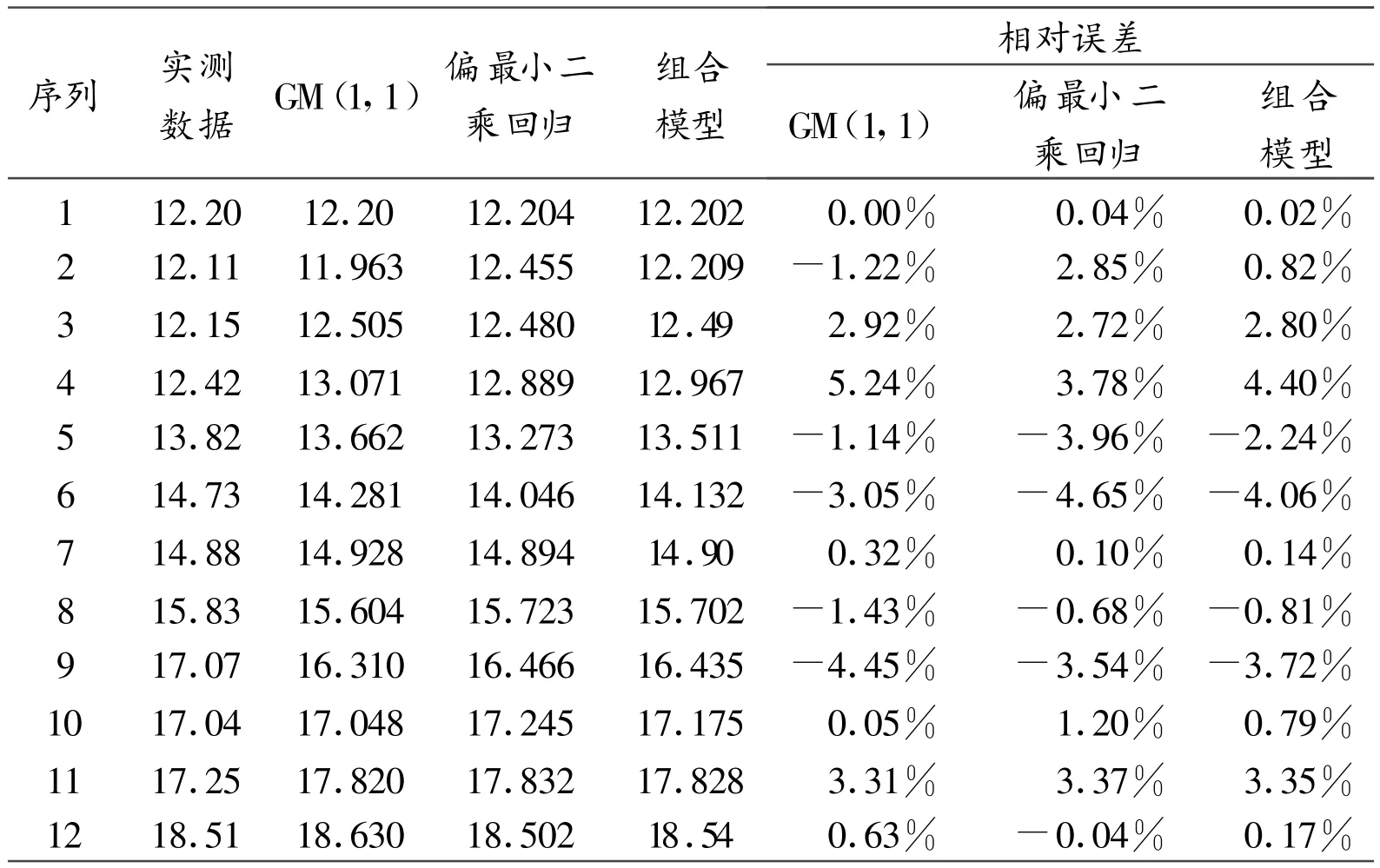
表2 三种模型的预测值与相对误差

由模拟结果可以看出：GM(1,1)模型最大相对误差为5.24%,最小相对误差为0.00%;偏最小二乘回归模型的最大相对误差为-4.65%,最小相对误差为0.04%;组合模型的最大相对误差为4.4%,最小相对误差为0.02%;组合预测模型的平均误差为最小。通过精度检验,模型等级为一级(好)。

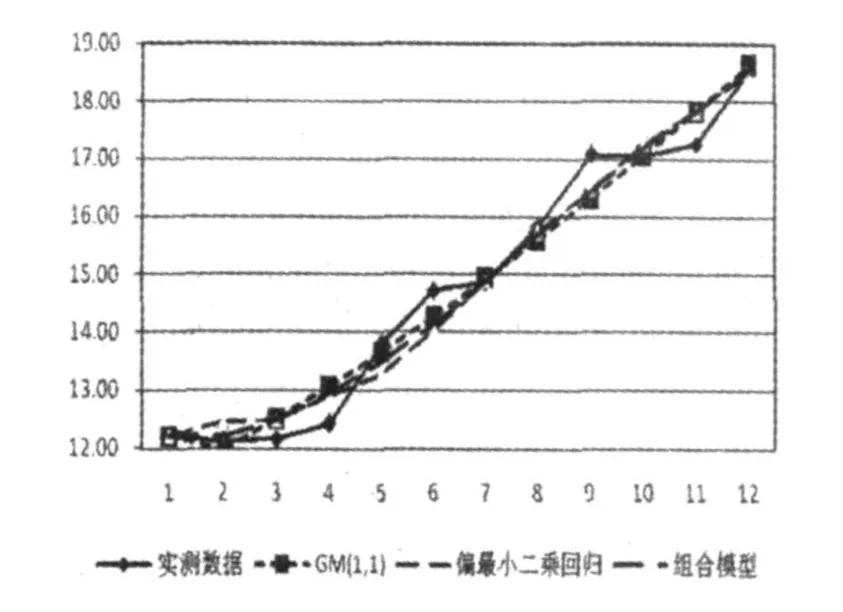
图1 实测数据与拟合值的比较

图2 相对误差的对比

3 结论

基于GM(1,1)模型及偏最小二乘回归分析模型的组合模型采用自适应和启发式算法,具有较强的动态适应性,用贝叶斯概率理论解决了模型中权重分配的不确定性。通过实例分析,此方法应用于燃气负荷预测中能有效地减小模型误差,因此可以用于燃气负荷预测领域。

[1] 傅立.灰色系统理论及其应用[M].北京：科学技术文献出版社,1992.

[2] 焦文玲,严铭卿,廉乐明.城市燃气负荷的灰色预测[J].煤气与热力,2001,21(5)：387-389.

[3] 严铭卿.燃气负荷中长期预测的方法[J].燃气技术,2009(10)：13-18.

[4] Bates J M,Granger C W J.Combination of forecasts[J].Operational Re-search Quarterly,1969,20(4)：451-468.

[5] 郑中为,史其信.基于贝叶斯组合模型的短期交通量预测研究[J].中国公路学报,2005,18(1)：85-89.

[6] 王惠文.偏最小二乘回归方法及其应用[M].北京：国防工业出版社,1999.

[7] 苗艳姝,段常贵.燃气年度负荷预测的偏最小二乘回归分析法[J].哈尔滨商业大学学报：自然科学版,2008,24(1)：95-96.

[8] 刘志谦,宋瑞,孙丽明.基于贝叶斯组合模型的物流预测与分析[J].技术与方法,2009,28(12)：116-117.