采用非线性变换的MPSK/MQAM符号速率盲估计

张海瑛，袁超伟

(1. 中国电子科技集团公司第五十四研究所 石家庄 050081; 2. 北京邮电大学信息与通信工程学院 北京 海淀区 100876)

采用非线性变换的MPSK/MQAM符号速率盲估计

张海瑛1，袁超伟2

(1. 中国电子科技集团公司第五十四研究所 石家庄 050081; 2. 北京邮电大学信息与通信工程学院 北京 海淀区 100876)

提出了一种采用非线性变换的MPSK/MQAM类信号符号速率盲估计方法，充分利用了MPSK/MQAM数字信号相邻符号的相位变化信息，通过对零中频信号进行非线性处理，构造一个非线性变换的复数函数，生成含有符号速率的离散谱线。利用四阶累积量的方法实现在强背景噪声下提取符号速率的基频分量。该方法运算简单，适应性好，对MQAM和MPSK调制的不同阶数、不同成形滤波器系数的信号均适用，低信噪比下仍具有很好的测量性能。

延时相乘; 四阶累积量; MPSK/MQAM信号; 非线性变换; 相位跳变; 符号速率估计

符号速率是解调器的重要参数，在电子对抗或智能接收系统中需要进行精确的估计。目前，符号速率的盲估计算法需要解决两个问题：(1)利用相位的跳变信息或信号的循环平稳特性提取符号速率的基频或谐频分量[1]；(2)利用信号的循环平稳特性抑制符号速率估计中的背景噪声[2]，以降低符号速率的检测门限。近年来，有许多文献提出了基于小波变换[3-4]、周期谱[5-6]、FFT变换[7-8]实现符号速率盲估计的算法，但这些方法存在无法适应低信噪比的要求、运算复杂度大等问题。

本文针对上述问题，提出了一种采用非线性变换的符号速率盲估计方法。该方法利用零中频变换和非线性变换，生成含有与符号速率相关的离散谱线信号，再利用四阶累积量一维切片提取符号速率的谐频分量。该方法运算简单、适应性好、抗噪声能力强，对MQAM和MPSK类中不同调制阶数、不同成形滤波器的信号均适用，在信噪比为5 dB时，对于高阶调制信号仍具有很好的性能。

1 符号速率离散谱线的生成

式中 Tb为符号周期；g(t)为长度为Tb的单位脉冲函数；fc为载波频率，该参数无需先验已知；nα、分别为星座映射的幅度值和相位值。

2 符号速率的提取

本文通过非线性变换产生含有信号符号速率的脉冲信号，在信噪比较高时，通过功率谱分析即可提取信号的符号速率，但功率谱方法不能有效地抑制高斯白噪声的影响。为了在低信噪比条件下精确地提取符号速率，可采用四阶累积量实现噪声的抑制。

假设接收机信号r(t)的背景噪声为高频带限复高斯噪声，其实部和虚部为相互独立且具有均值为0和方差为的窄带高斯过程，设

将信号经过零中频下变频和非线性变换，去掉加噪信号中的幅度项影响，留下其相位噪声；经过延迟相乘的变换，对于相位项的噪声也仅是相减的运算，此时仅需分析加噪信号的相位分布。为简化推导过程，通过分析正弦信号加高斯噪声的联合概率密度p(ρy, ϕy)分析相位分布。设信号幅度为a，则有：

3 算法流程

4 计算机仿真及性能分析

4.1 加性噪声的影响分析

本文进行的第一种试验条件如下：以16QAM信号为例，成形滤波器系数 =0.5、fs=1、fc=0.25、fb=0.062 5。共进行500次独立试验，每次试验的符号个数为1 000。通过对四阶累积量的一维切片进行FFT计算，可以检测出功率谱上的离散谱线，从而判断出信号的符号速率。在SNR=−3 dB时，其四阶累积量的一维切片 c4,x(τ,τ, 0 )的功率谱如图1所示，仍可以准确地检测出信号的符号速率。

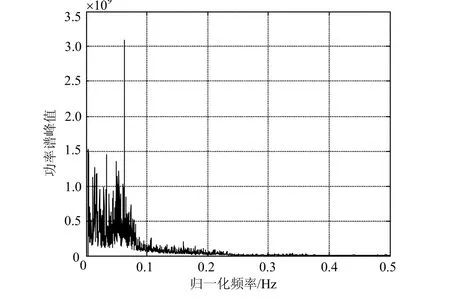
图1 SNR=−3 dB时， c4,x(τ,τ, 0 )的功率谱

本文进行的第二种试验条件如下：成形滤波器系数 =0.5、 fs=1、 fc=0.25、 fb=0.062 5。QPSK、8PSK、16QAM 和64QAM 四类信号随信噪比的变化估计性能的结果如图2所示。QPSK和16QAM的性能曲线比较接近，在SNR=0 dB时，估计正确率可以达到90%以上；8PSK和64QAM的性能曲线比较接近，当SNR＞5 dB时，估计正确率可以达到95%以上。由此可见，该算法对高阶 MPSK/MQAM 调制也具有较强的适应能力。本文定义符号速率的相对估计误差在0.1%内为估计正确。

图2 不同信噪比下不同信号的符号速率的估计正确率曲线

4.2 成形滤波器系数的影响分析

以16QAM信号为例， 0.5、fs=1、fc=0.25、fb=0.062 5，选择升余弦成形滤波器。成形滤波器系数 分别取0、0.25、0.50、0.75、1.00，随信噪比变化的估计性能结果如图3所示。在α=0的极限情况下，该算法无法生成离散的符号速率的谱线峰值，因为信号此时由离散相位变成了连续相位，即便信噪比很好，也很难实现符号速率的正确估计。当α> 0 .1时，可估计出信号的符号速率，且系数越大，估计性能越好。

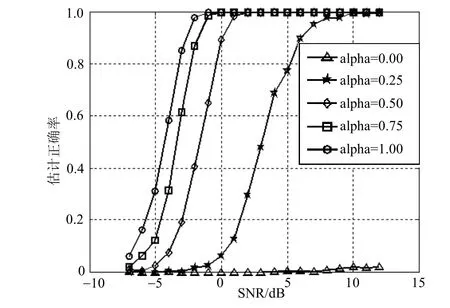
图3 成形滤波器系数不同时符号速率的估计正确率曲线

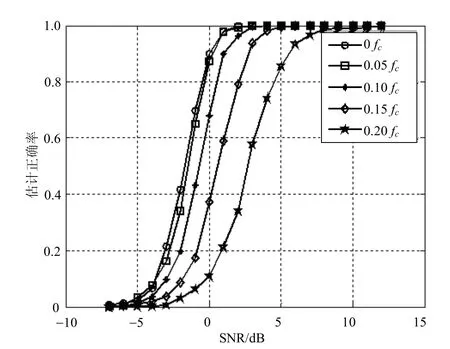
图4 载频偏差不同下16 QAM符号速率的估计正确率曲线

4.3 载频偏差对估计精度的影响分析

以16QAM信号为例， =0.5、fs=1、fc=0.25、fb=0.062 5。载频偏差Δf分别为0、0.05fc、0.1fc、0.15fc、0.2fc时，随信噪比变化的估计性能结果如图4所示。由图可知，该算法在载波估计偏差20%以内时，性能都很好。该算法中通过数字下变频和去均值等运算，能够有效地校正由频率偏差而造成的直流分量，理论和实验仿真都证明了该方法的有效性。

4.4 几种算法的性能比较

为了评估本文算法的性能，通过计算机仿真文献[6](基于循环相关方法cyclo)和文献[4](基于小波变换方法wavelet)两种符号速率盲估计算法。以8PSK信号为例，α=0.5、 fs= 1 、 fc=0.25、fb= 0 .062 5、L= 1 000。文献[6]方法中，循环谱计算时Δf = 0 .062 5、 Δ α = 1 /102 4；文献[4]方法中，小波变换的尺度选为20。在500次独立实验中得到SNR在0～15 dB范围内符号速率估值相对误差的均值结果，如图5所示。

图5 不同估计方法的性能对比

实验表明，本文算法的性能明显优于其他两种算法，主要是由于该算法通过对中频信号的下变频和非线性处理还原出信号的相位信息，又通过延迟相乘获得相邻符号之间相位差的绝对值，在幅度谱上产生了与符号速率相对应的离散频率分量，有利于对相位跳变信息的提取和窄带噪声的抑制。另外，利用四阶累积量一维切片能够有效抑制高斯背景噪声的特点，进一步抑制了噪声的影响，提高了测量的精度。

5 结 论

本文算法通过非线性变换产生出对应于符号速率的基频分量和谐波分量，利用高阶谱处理技术在抑制高斯背景噪声的同时，有效地检测出MPSK和MQAM信号的相位跳变信息，即信号的符号速率。理论分析和计算机仿真均验证了该算法的正确性和有效性。仿真结果表明本文算法无须知道信号的调制方式和精确的载频等先验条件，运算简单，适应性好，对MQAM和MPSK调制的不同阶数、不同成形滤波器系数的信号均适用。

[1]LOPEZ-VALCARCE R, SCALISE S, MOSQUERA C.Non- data-aided symbol rate estimation of linearly modulated signals[J]. IEEE Transaction on Signal Processing, 2008, 56(2): 664-674.

[2]刘双平, 闻 翔, 金 梁. 一种抑制符号速率估计背景色噪声的非线性滤波算法[J]. 电子学报, 2007, 35(1):95-99.

LIU Shuang-ping, WEN Xiang, JIN Liang. A new nonlinear filtering algorithm for colored background self-noise suppressing of symbol rate estimation[J]. Acta Electronica Sinica, 2007, 35(1): 95-99.

[3]HO K C, PROKOPIW W, CHAN Y T. Modulation identification of digital signals by the wavelet transform[J].IEE Proceedings on Radar, Sonar and Navigation, 2000,147(4): 169-176.

[4]YOUSSEF O A S. New algorithm to phase selection based on wavelet transforms[J]. IEEE Transactions on Power Delivery, 2002, 17(4): 908-914.

[5]刘世刚. 基于循环相关的符号速率盲估计[J]. 信号处理,2004, 20(4): 356-359.

LIU Shi-gang. Cyclocorrelation based symbol rate estimation [J]. Signal Processing, 2004, 20(4): 356-359.

[6]JIN Yan, JI Hong-bing. Statistical characteristics of stationary processes in cyclic autocorrelation based PSK symbol rate estimation[C]//Control Conference, CCC 2007.[S.l.]: [s.n.], 2006.

[7]FLOHBERGER M, KOGLER W, GAPPMAI W, et al.Symbol rate estimation with inverse fourier transforms[C]//2006 International Workshop on Satellite and Space Communications. Madrid: IWSSC, 2006.

[8]XU Hai-yuan, ZHOU Yi-yu, HUANG Zhi-tao. Blind roll-off factor and symbol rate estimation using FFT and least squares estimator[C]//2007 International Conference on Wireless Communications, Networking and Mobile Computing. [S.l.]: [s.n.], 2007.

[9]鞠德航, 林可祥, 陈 捷. 信号检测理论导论[M]. 北京:科学出版社, 1977.

JU De-hang, LIN Ke-xiang, CHEN Jie. Introduction on signal detection theory[M]. Beijing: Science Press, 1977.

[10]畅艺峰, 李存永. 不同注入脉冲信号的功率谱计算[J].电子与信息学报, 2007, 29(5): 1250-1253.

CHANG Yi-feng, LI Cun-yong. New approach to the power spectrum calculation of several injection signals[J].Journal of Electronics & Information Technology, 2007,29(5): 1250-1253.

[11]周 围, 林 云, 张德民, 等. 智能天线中一种上行信号空间特征盲估计算法[J]. 北京邮电大学学报, 2006,29(6): 32-35.

ZHOU Wei, LIN Yun, ZHANG De-min, et al. A blind estimation algorithm for spatial signature of uplink signals in smart antenna[J]. Journal of Beijing University of Posts and Telecommunications, 2006, 29(6): 32-35.

编 辑 黄 莘

Blind Estimation of MPSK/MQAM Symbol Rate with Nonlinear Processing

ZHANG Hai-ying1and YUAN Chao-wei2

(1. China Electronics Technology Group Corporation No.54th Research Institute Shijiazhuang 050081;2. Institute of Information and Communication, Beijing University of Posts and Telecommunications Haidian Beijing 100876)

A blind method for symbol rate estimation of MPSK/MQAM signals by using the nonlinear process is presented. Utilizing the phase changing between inter-symbols and through the nonlinear transforming of zero IF signals, the spectral lines corresponding to the symbol rate can be extracted. The fourth-order cumulant is used for suppressing the strong background noise of symbol rate spectral lines in this paper. This method is robust to Gaussian noise and can achieve good estimation results with lower SNR. At the same time, it has lower computational complexity and is applicable to different shaping filters and different modulation orders of MPSK/MQAM signals.

delay multiplication; fourth-order cumulant; MPSK/MQAM signals; nonlinear transform;phase change; symbol rate estimation

TN911.72

A

10.3969/j.issn.1001-0548.2010.06.004

2009- 06- 10;

2009- 11- 20

国家自然科学基金(60672132)

张海瑛(1973- )，女，博士，研究员级高级工程师，主要从事通信对抗和信号处理等方面的研究.