泛函网络模型及应用研究综述

周永权，赵 斌

(1. 广西民族大学数学与计算机科学学院 南宁 530006; 2. 中央民族大学理学院 北京 海淀区 100083)

泛函网络模型及应用研究综述

周永权1，赵 斌2

(1. 广西民族大学数学与计算机科学学院 南宁 530006; 2. 中央民族大学理学院 北京 海淀区 100083)

回顾了近年来泛函网络模型及应用的研究进展，首先根据泛函网络模型结构的特点，将现有的泛函网络模型归结为两类典型的泛函网络模型；其次，给出一般泛函网络模型的学习过程；然后从时间序列分析、差分方程、CAD、非线性回归、数值优化计算、非线性系统辨识、检测和预测、复杂系统建模8个方面，介绍了泛函网络的应用现状；最后评述了泛函网络今后的研究方向和研究内容。

泛函网络; 学习过程; 优化问题; 典型泛函网络

泛函网络(functional network，FNt)[1]是人工神经网络(artificial neural network，ANN)的一种拓展，它处理的仅是一般实泛函模型。与ANN不同，泛函网络神经元之间无联接权值，神经元函数不固定，是可学习的。泛函网络通常是一些给定的基函数簇的线性组合，在实际应用中可根据所求问题的物理背景知识和结构学习评价准则，选择不同的基函数簇(如多项式、三角函数、Fourier函数等)实现用较小的网络规模获得更满意的泛化特性。

学者们提出的多种类型泛函网络，归结起来，可分为可分离泛函网络模型和可结合泛函网络模型，这些模型在应用方面都取得了较大的成功。例如，文献[2-5]将泛函网络应用于线性及非线性回归、非线性系统辨识和混沌时间序列预测，以及泛函方程求解等领域；文献[6-7]将泛函网络应用于B样条曲面重构问题及海洋捕鱼技术；文献[8]将泛函网络应用于实时洪水预测；文献[9]将泛函网络应用于故障检测；文献[10]将泛函网络和不变性分析结合用应于特征选择问题；文献[11]将泛函网络应用于分类及回归问题；文献[12]将泛函网络、最小均方差逼近和遗传算法结合形成一种混合算法，并将其用于求解三维点集的Bézier曲线和曲面拟合问题；文献[13]提出了复杂泛函网络的进化工程；文献[14]将可结合泛函网络应用于植物生长动态建模；文献[15]将泛函网络应用于软件可靠性分析；文献[16]又将泛函网络应用于矿山机械参数的优化设计。

在国内，文献[17]提出基于泛函网络的数值近似方法；文献[18]给出了非线性系统辨识的一种泛函网络方法，其基本原理是网络参数利用梯度下降法进行学习，该辨识方法具有较快的收敛速度和较优的性能；文献[19-22]提出了层次泛函网络整体学习算法、复值可分离的泛函网络学习算法、基于泛函网络的多项式Euclidean算法和新型Sigma-Pi泛函网络模型，这些方法能够快速地获得所求问题的精确解；文献[23]提出了基于多输入泛函网络的构造和学习策略，将泛函网络拓扑结构看成是若干子泛函网络模型的集成，分别对各个子泛函网络进行研究；文献[24]提出了fuzzy插值及其fuzzy泛函网络构造理论，从理论上证明了泛函网络能够以任意精度逼近任意定义在有界闭集上的连续函数；文献[25]用递归泛函网络、序列泛函网络模型及其学习算法解决了传统的数值方法难以求解泛函方程这个难题；文献[26]提出基于遗传规划实现泛函网络神经元的函数类型优化方法，可实现对神经元函数类型的优化；文献[27]提出了泛函网络与模糊逻辑推理及支持向量机之间的等价关系。

研究表明，泛函网络不仅表现在ANN可以解决的问题泛函网络同样可以解决，而且对于某些ANN不能解决的问题泛函网络也可解决，泛函网络的性能在很多方面优于人工神经网络。目前，泛函网络以其独特的拓扑结构和处理信息方法，已在混沌时间序列预测、微分、差分方程求解、曲面重构、线性、非线性回归、故障诊断、工程结构优化设计、水资源预测、生物医学工程等许多应用领域中展现出了卓越性能。

本文首先根据泛函网络模型结构的特点，将现有的泛函网络模型归结为2类典型的泛函网络模型，然后从时间序列分析、差分方程、CAD、非线性回归、数值优化计算、非线性系统辨识、检测和预测、复杂系统建模8个方面，介绍了近年来泛函网络的应用现状；最后评述了泛函网络今后的研究方向和研究内容。

1 典型的泛函网络模型

1.1 泛函网络基本组成

图1是一个典型的泛函网络模型[2]。

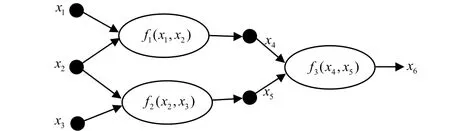
图1 一个典型的泛函网络拓扑结构模型

一般泛函网络组成包括：(1)输入层是输入数据的一层单元，如图1中的 { x1,x2,x3} ；(2)神经元中的每一个神经元是一个计算单元，计算一组来自前一层神经元或输入单元的输入值，为给下一层神经元或输出单元提供一组输入数据，如图1中的 { f1,f2}和{f3}；(3)中间存贮单元层存储由神经元产生的信息，用于存储神经元 { f1,f2}产生的信息，如图1中的{x4, x5}，即 x4=f(x1,x2)、x5= f(x2,x3)；(4)有向连接线将输入层、第一层神经元、第二层神经元、……、最后一层神经元及输出单元连接起来，箭头表示信息流动的方向；(5)输出层最后一层单元，输出网络的结果数据，比如图1中的{x6}，输出信息 x6= f3( x4, x5)= f3( f1(x1,x2), f2( x2, x3))。

所有这些元素组合在一起就形成了泛函网络结构，确定了网络的泛函能力。网络的结构是指神经元的组织及包含的连接。

1.2 泛函网络拓扑结构类型

1.2.1 一般泛函网络模型

一般地，n层泛函网络的模型可表示为：

对应的网络结构如图2所示：

图2 一般泛函网络的拓扑结构

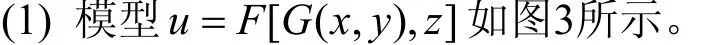
图3 模型 u =F[G(x,y),z ]

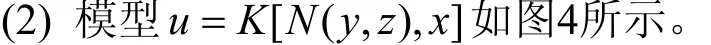
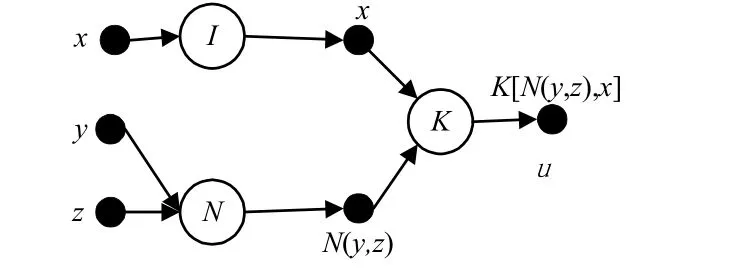
图4 模型 u =K[N(y,z),x]

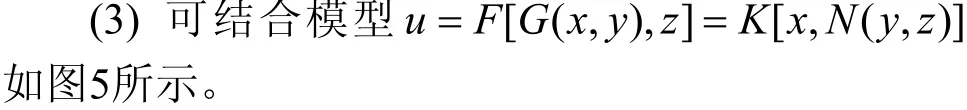
图5 可结合泛函网络模型

该网络模型表示的泛函方程为：

1.2.3 可分离泛函网络模型

可分离泛函网络是在泛函网络中应用最为广泛的一种模型，它的泛函表达式是各输入变量分离作用效果的组合，其网络模型如图6所示。

图6 可分离泛函网络模型

该网络表示的泛函方程为：

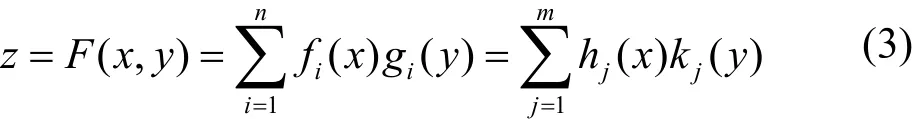
2 泛函网络学习过程

人工神经网络是对权值的学习，而泛函网络是对网络结构和参数的学习。学习方法可分为精确学习和近似学习两种。精确学习就是确定泛函网络所表示的泛函方程的解函数，近似学习就是依据给定样本数据评价神经元函数。其基本方法是线性组合基函数簇的函数，并优化线性组合的系数。以下介绍泛函网络的学习步骤。

(1)确定网络初始结构。根据问题本身的知识和信息(已知数据、问题的先验知识及函数的某些特性等)，设计出初始的泛函网络拓扑结构。

(2)简化网络结构。每一初始网络结构对应一泛函方程，利用泛函方程解的特性找出与初始网络结构等价的泛函网络类，并从中选择与其等价的简单网络结构。

(3)表达式的唯一性。在泛函网络学习之前，确保网络输出表达式的唯一性，即对于一给定的泛函网络拓扑结构，在相同的初始条件，使得对于任意的输入值，网络都有相同的输出值。

(5)模型选择。对泛函网络学习需要考虑选取何种类型的基函数簇，一旦选定了基函数，考虑在基函数中如何选取函数项。关于问题，即泛函网络结构学习评价问题，能否找到一行之有效方法来评价泛函网络结构学习的性能，至今还没有彻底解决。文献[2]虽给出了5种方法，但在实际应用中，存在着计算量大、使用不方便等不足。

(6)模型测试。对网络学习效果进行测试，学习样本数据一部分用于学习，一部分用于测试。

下面通过一简单例子说明泛函网络学习过程。

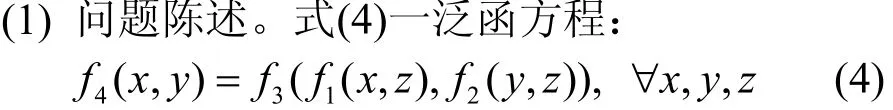
(2)初始拓扑结构：其对应的网络结构如图7所示。

图7 对应于(4)式的泛函网络结构

(3)结构学习。式(4)给出了函数 f1、f2、f3和 f4的约束条件，可简化其泛函结构。泛函方程式(4)在实数矩阵连续的一般解为：

式中1F、F2、、F6是任意连续且严格单调函数。将式(5)代人式(4)，得到泛函方程(5)的最简单表达式

简化后的泛函网络如图8所示。

图8 式(4)简化后的泛函网络

(4)表达式唯一性。泛函方程式(4)在实数矩形连续的一般解为式(5)，式(4)给出了函数 f1、f2、f3和f4的约束条件，经过式(5)的形式转换，无论初始条件为保，式(4)与式(6)得出的函数表达式是一样的，即简化后的泛函网络与初始的泛函网络是等价的，所以初始条件不是必需的。

式中 系数aji是泛函网络的参数。当选定了合适的基函数簇后，对神经元函数的学习便转化为对网络参数aji的学习。以下我们用线性学习方法：

对于图8的网络结构，假设对于输入 、y和输出u，构造的函数为：

3 泛函网络应用进展

尽管泛函网络的类型不同，但在自适应性、学习能力、线性与非线性、容错性、并行性等方面有一定的共性。本文从以下8个方面介绍泛函网络的应用现状。

3.1 时间序列分析

时间序列分析是根据系统观测得到的时间序列数据，通过曲线拟合和参数估计建立数学模型的理论和方法，一般采用曲线拟合和参数估计方法(如非线性最小二乘法)进行。而传统的曲线拟合和参数估计方法普遍存在着在人为给定所拟合曲线结构的基础上，对参数进行确定，所获得结果要么误差过大；要么不符合客观实际。泛函网络提供一种新的曲线结构拟合方法，结构和参数共同学习，最终实现结构和参数最优。文献[2]基于泛函网络的结构特点建立学习模型，针对一元Box-Jenkins 时间序列模型、多元Box-Jenkins时间序列模型、经济预测问题、混沌时间序列模型等，给出了一系列泛函网络求解时间序列的方法，取得了较大的成功。

3.2 差分、泛函方程

差分方程反映的是关于离散变量的取值与变化规律。差分方程就是针对要解决的目标，引入系统或过程中的离散变量，根据实际背景的规律、性质、平衡关系，建立离散变量所满足的平衡关系等式，从而建立差分方程，求出和分析方程的解，或者分析得到方程解的。差分方程模型有着非常广泛的实际背景，在经济金融保险领域、生物种群的数量结构规律分析、疾病和病虫害的控制与防治、遗传规律的研究等许许多多的方面都有着非常重要的作用。可以说，只要牵涉到关于变量的规律、性质，就可以适当地用差分方程模型来表现与分析求解。

基于泛函网络结构特点，建立学习模型，文献[2]给出了一种泛函网络求解差分方程新方法；针对泛函方程求解目前还没有行之有效的方法，文献[25]提出了序列泛函网络模型和学习算法，针对经典的9类泛函方程，给出了一求解的新方法，该方法也可用于求解一般泛函方程。

3.3 CAD

曲面重构是逆向工程的关键，也是当前研究的热点，如何解决曲面重构的速度和精度，是曲面重构技术的核心和关键，也是各种算法所追求的最终目的。基于泛函网络结构特点建立学习模型，文献[2]针对所构造曲线方程 f (x,y,z)= 0 ，提出了一种基于泛函网络曲面重构方法；该方法最大的特点是通过学习训练，能获得 f (x,y,z)= 0 的显示函数的近似表达式；基于同样的思想，文献[6]将泛函网络应用于B样条曲面重构问题。

3.4 线性、非线性回归

对于非线性模型的回归问题，一般先将其化为线性模型，然后再用最小二乘法求出参数的估计值，最后再经过适当的变换，得到所求回归曲线。传统确定曲线类型的方法是一般从两个方面考虑；(1)根据专业知识，从理论上推导或凭经验推测；(2)在专业知识无能为力的情况下，通过绘制和观测散点图确定曲线大体类型。但传统方法给人们的应用带来了新的困难。于是，文献[2]给出了基于泛函网络的线性、非线性回归方法，克服了目前传统非线性回归问题所存在的不足。

3.5 数值优化计算

随着计算机技术的飞速发展，计算数学也得到了很大的发展。随着研究的深入，人们发现传统的数值方法存在着许多不足。比如，传统的数值方法是一种串行结构的算法，相对于并行结构算法，其效率会低很多。而且，传统算法的优化结果依赖于初值，如果初值选取不当，算法收敛速度慢，甚至可能发生不收敛现象。于是，文献[17]提出基于泛函网络的数值近似方法。文献[29-30]针对在科学计算、工程技术应用领域中常用的数值积分、级数展开等问题，提出了一种基于泛函网络模型的数值积分方法，该方法可以求解任意函数的数值积分，且积分求解结果优于其他方法。针对多重数值积分，在构造性地证明了层次泛函网络具有全局逼近性的基础上，将层次泛函网络应用于求解多重数值积分，得到比较高的计算精度。另外，提出了一种基于泛函网络的函数级数展开方法，并分别就一元和多元函数的级数展开，给出了对应的泛函网络模型和学习算法。

3.6 非线性系统辨识

系统辨识是控制理论研究的主要内容之一。近年来,非线性系统的辨识问题受到广泛关注，人们在努力寻找一种本质上能够描述任意非线性系统的模型以及相应的逼近算法。神经网络、小波和模糊等是目前研究得比较多的内容。神经网络由于具有较好的逼近能力和内在的自适应特征而被广泛用于系统辨识。但由于实际中神经网络存在结构过于复杂、结点过多，并且在学习过程中容易陷入局部极小点而导致逼近能力有限等问题，因而在对一些复杂系统建模时，常存在较大的建模误差。文献[18]提出了一种基于泛函网络的非线性系统的辨识方法，而网络参数利用梯度下降方法进行学习。该基于泛函网络的辨识方法具有收敛速度快，逼近能力强等优点，为非线性系统辨识提供了一种新方法。

3.7 检测与预测

目前常用的预测方法有基于神经网络的预测算法和基于自适应滤波器的预测算法。基于神经网络的预测算法，其优点是可任意逼近非线性，缺点是计算复杂、运算量大，不宜于数字化实现。因此，寻找一种计算模型简单、运算量少的检测与预测方法，有着极为重要的应用价值。文献[7]提出一种基于泛函网络的预测鱼群模型及方法，并与和神经网络技术作比较表明。泛函网络模型简单、计算量小。文献[15]将泛函网络应用于软件可靠性分析；文献[16]将泛函网络应用于矿山机械参数设计；文献[8]将泛函网络应用于实时洪水预测等。

3.8 复杂系统建模

系统仿真技术正面临着新的挑战，即如何建立基于演化的复杂系统动力学的建模与仿真方法。该领域的工作主要内容包括：复杂性问题的提出；主要命题；复杂系统的动力学特征；复杂系统建模与仿真的理论研究、方法和软件。文献[14]将广义可结合泛函网络应用于植物生长动态建模，提出了一种新的统计技术——Bayesian广义可结合泛函网络，给出了在温室条件下的植物生长动态模型，该模型能将知识和数据有机地结合起来，通过对网络的学习和训练，完成植物生长动态建模。

4 结 束 语

泛函网络作为计算智能学科一个崭新的研究方向，其一些理论和应用基础并不完善，需要人们不断地完善基础理论和提出更适于所要解决的问题的新的网络结构及新的算法。关于泛函网络今后的研究方向和研究内容，笔者认为可从以下几方面进行深入探讨：

(1)尽管泛函网络在多方面应用均取得了比神经网络更优的效果，但仍受到神经网络一些固有缺陷的限制，需要将问题的解映射成合适的泛函网络描述，还需考虑网络结构和参数的影响，使泛函网络问题比较复杂。应进一步研究简化泛函网络结构，以易于其算法计算和硬件实现。

(2)由于每一泛函网络对应着一泛函方程，泛函方程的解用于简化泛函网络的拓扑结构，因此，寻找一种高效的泛函方程求解算法，有着重要的理论意义。

(3)在泛函网络应用的多个方面，注重将泛函网络与现有的其他群智能技术相结合，如分形、小波、进化计算、群智能算法等，以便形成智能泛函网络。

[1]CASTILLO E. Funetional networks [J]. Neural Proeessing Letters, 1998, 7: 151-159.

[2]CASTILLO E, COBO A, GUTIERREZ JM, et al.Functional networks with applications[M]. Boston: Kluwer Aeademic Publishers, 1999.

[3]CASTILLO E, HADI A S, et al. Semi-parametric nonlinear regression and transformation using functional networks[J].Computational Statistics & Data Analysis, 2008, 52:2129-2157.

[4]CASTILLO E, GUTIérrez J M. Nonlinear time series modeling and prediction using functional networks.Extracting Information M asked by Chaos[J]. Physics Letter Apply, 1998, 244: 71-84.

[5]CASTILLO E, COBO A, GutiÉrrez J M. Working with differential, functional and difference equation using functional networks[J]. Applied Mathematical Modeling,1999, 23: 89-107.

[6]IGLESIAS G A. ECHEVARR´ıa, A. G´Alveza. Functional networks for B-spline surface reconstruction[J]. Future Generation Computer Systems, 2004, 20: 1337-1353.

[7]ALFONSO I, BERNARDINO A, CTOS J M, et al. A comparison between functional networks and artificial neural networks for the prediction of fishing catches[J].Neural Computer & Applied, 2004, 13: 24-31.

[8]MICHAEL B, YANG Jian-qing. Functional networks in real-time flood forecasting—a novel application[J].Advances in Water Resources, 2005, 28: 899-909.

[9]OSCAR F R, CASTILLOB E, AMPARO A B, et al. A measure of fault tolerance for functional networks[J].Neurocomputing, 2004, 62: 327-347.

[10]NOELIA S M, MARía C F, CASTILLO E. Functional networks and analysis of variance for feature selection[J].IEEE Press, 2006, 4224: 1031-1038.

[11]BEATRIZ L, ANA P P. Functional networks for classification and regression problems[C]//International Conference on Mathematical and Statistical Modeling in Honor of Enrique Castillo, Department of Statistical Methods. Manama, Bahrain: [s.n.], 2006: 28-30.

[12]AKEMI G, ANDRés I, ANGEL C. Bézier curve and surface fitting of 3D point clouds through genetic algorithms[J]. Lecture Notes in Computer Science, 2007,4706: 680-693.

[13]PABLO K, HIROSHI K, MIKHAILOV A S. Evolutionary engineering of complex functional networks[J]. IEEE Press,2007, 4308: 1011-1019.

[14]QU Han-bing, HU Bao-gang. Variational learning for generalized associative functional networks in modeling dynamic process of plant growth[J]. Ecological Informatics,2009, 4: 163-176.

[15]EMAD A E. Functional networks as a novel data mining paradigm in forecasting software development efforts[J].Expert Systems with Applications, 2010.

[16]EMAD A E, ASPAROUHOV O, ABDULRAHEEM A. On utilizing functional networks computational intelligence in forecasting rock mechanical parameters for hydrocarbon reservoirs: methodology and comparative studies[C]//AAPG GEO 2010 Middle East Geoscience Conference &Exhibition, Innovative geoscience solutions-meeting hydrocarbon demand in changing times. Manama, Bahrain:[s.n.], 2010: 7-10.

[17]王东平, 周尚波, 虞厥邦. 基于泛函网络的数值近似方法[J]. 四川大学学报(自然科学版), 2001, 38(5): 658-661.

WANG Dong-ping, ZHOU Shang-bo, YU Jue-bang.Numerical approximation based on a functional network[J].Journal of Sichuan University (Natural Science Edition).2001, 38(5): 658-661.

[18]李春光, 廖晓锋, 何松柏, 等. 非线性系统辨识的一种泛函网络方法[J]. 系统工程与电子技术, 2001, 23(l): 50-53.

LI Chun-guang, LIAO Xiao-feng, HE Song-bai, et al.Functional network method for the identification of nonlinear systems[J]. Systems Engineering and Electronics,2001, 23(l): 50-53.

[19]周永权, 焦李成. 层次泛函网络整体学习算法[J]. 计算机学报, 2005, 28(8): 1277-1286.

ZHOU Yong-quan, JIAO Li-cheng. Universal learning algorithm of hierarchical function networks[J]. Chinese Journal of Computer, 2005, 28(8): 1277-1286.

[20]周永权, 赵 斌, 焦李成. 一种复值可分离的泛函网络学习算法[J]. 系统工程与电子技术, 2006, 28(8): 1244-1248.

ZHOU Yong-quan, ZHAO Bin, JIAO Li-cheng. Learning algorithm for separable complex-valued functional networks[J]. Systems Engineering and Electronics, 2006,28(8): 1244-1248.

[21]周永权, 焦李成, 李陶深. 一种基于泛函网络的多项式Euclidean算法[J]. 计算机科学, 2006, 33(9): 131-134.

ZHOU Yong-quan, JIAO Li-cheng, LI Tao-shen. A learning algorithm of euclidean based on functional networks[J].Computer Science, 2006, 33(9): 131-134.

[22]周永权, 陈东用, 李陶深. 新型Sigma-Pi泛函网络模型[J]. 计算机工程, 2006, 32(19): 196-198.

ZHOU Yong-quan, CHEN Dong-yong, LI Tao-shen. New sigma-pi functional networks model[J]. Computer Engineering, 2006, 32(19): 196-198.

[23]崔明义, 张新祥. 基于多输入泛函网络的构造和学习策略[J]. 计算机科学, 2006, 33(10): 169-191.

CUI Ming-yi, ZHANG Xin-xiang. Strategy of structuring and learning based on multi-Input and single output functional network[J]. Computer Science, 2006, 33(10):169-191.

[24]周永权, 焦李成, 李陶深. Fuzzy插值及其Fuzzy泛函网络构造理论[J]. 计算机科学, 2007, 34(7): 5-9.

ZHOU Yong-quan, JIAO Li-cheng, LI Tao-shen. Fuzzy interpolation and fuzzy functional network constructive theory[J]. Computer Science, 2007, 34(7): 5-9.

[25]周永权, 赵 斌, 焦李成. 序列泛函网络模型及其学习算法与应用[J]. 计算机学报, 2008, 31(7): 1073-1081.

ZHOU Yong-quan,ZHAO Bin, JIAO Li-cheng, Serial function networks method and learning algorithm with applications[J]. Chinese Journal of Computer, 2008, 31(7):1073-1081.

[26]周永权, 焦李成. 基于遗传规划实现泛函网络神经元的函数类型优化[J]. 计算机科学, 2007, 34(2): 7-9.

ZHOU Yong-quan, JIAO Li-cheng. Optimizing neuron function types based on GP in functional network design[J].Computer Science, 2007, 34(2): 7-9.

[27]周永权, 李陶深, 张显全. 泛函网络与模糊逻辑推理及支持向量机之间的等价关系[J]. 计算机学报(已录用).

ZHOU Yong-quan, LI Tao-shen ZHANG Xian-quan.The relationship among functional network and fuzzy logic systems with SVM[J]. Chinese Journal of Computer,2010(Accept).

[28]周永权. 泛函网络理论及其学习算法研究[D]. 西安: 西安电子科技大学, 2006.

ZHOU Yong-quan. Functional network theory and learning algorithms[D]. Xi’an: Xidian University Press, 2006.

[29]韦修喜, 周永权, 蓝晓玲. 一种基于泛函网络求数值积分方法研究[J]. 计算机科学, 2009, 36(4): 224-226，238.

WEI Xiu-xi, ZHOU Yong-quan. LAN Xiao-ling.Numerical integration method study based on function network[J]. Computer Science, 2009, 36(4): 224-226, 238.

[30]韦修喜, 周永权, 李陶深. 层次泛函网络构造理论及其在多重数值积分中的应用[J]. 计算机应用, 2008, 28(10):2711-2714.

WEI Xiu-xi, ZHOU Yong-quan, LI Tao-shen. Construct theory of hierarchical functional networks and its application in multiple numerical integral[J]. Journal of Computer Applications, 2008, 28(10): 2711-2714.

编 辑 蒋 晓

Progress of Functional Networks and Their Applications

ZHOU Yong-quan1and ZHAO Bin2

(1. College of Mathematics and Computer Science, Guangxi University for Nationalities Nanning 530006;2. School of Science, Central University for Nationalities Haidian Beijing 100081)

The research progress and applications of functional networks (FNt)models in recent years are reviewed. At first, according to the functional network model structure characteristics, FNt models are classified into two typical types in accordance with the functional networks. Secondly, recent applications of FNt are introduced in many fields, such as times series analysis, differential equations, CAD, nonlinear regression,numerical optimize computation, nonlinear system identification, detection and prediction, complex system modeling, etc. Finally, some remarks on the further research and directions of FNt are presented.

functional networks; learning process; optimization problem; typical type functional networks

TP18

A

10.3969/j.issn.1001-0548.2010.06.001

2010- 09- 15

国家自然科学基金(60461001)；广西自然科学基金(0991086)；国家民委科研资助项目(08GX01)

周永权(1962- )，男，博士，主要从事计算智能、神经网络及应用方面的研究.

·通信与信息工程·