标准模型下可证安全的一种新的CL-PKE加密方案
2010-02-08徐秋亮
杨 勇,徐秋亮
(山东大学计算机科学与技术学院 济南 250101)
标准模型下可证安全的一种新的CL-PKE加密方案
杨 勇,徐秋亮
(山东大学计算机科学与技术学院 济南 250101)
该文在标准模型下构建了一个实用的无证书公钥加密体制(CL-PKE),相比于其他的CL-PKE加密体制,该体制在加密时没有椭圆曲线上的对运算,而且所基于的难解性问题假设是自然的双线性Diffie-Hellman(BDHP)问题。为提高安全性,该文的安全模型选用了标准模型下的选择性身份(Selective-ID)模型,在提高效率的同时也增强了安全性。
算法; 双线性Diffie-Hellman问题; 无证书公钥加密; 公钥密码学; 标准模型
文献[1]提出了CL-PKE(certificateless encryption scheme)无证书加密体制,该体制的目的在于增强基于身份的加密体制,使基于身份的加密体制可以阻止密钥生成中心KGC的伪造攻击。CL-PKE加密体制就集成了传统PKE加密体制和基于身份加密体制的优势,具有阻止KGC伪造攻击和无公钥证书的特点。
最初的CL-PKE加密体制都是基于Random Oracle模型的[1-2],之后有学者提出了基于标准模型的加密算法,但基于标准模型的加密算法大都有着复杂的运算和经过变形的困难性问题假设[1-3]。在具体算法发展到一定程度后,有的学者又提出了基于各种模型的通用算法[2,4-5],但有些通用算法在某些模型下被证明是错误的[6],因此,需要进一步研究构建基于一定模型的好的通用算法。
相对于本文来讲,在[JCH07]方案中,虽然加密时没有对运算,但在检验用户公钥时有两个对运算[7],[BSN05]的方案虽然没有椭圆曲线上的对运算,效率较高,但要求在产生用户公钥前必须先产生一个部分用户公钥[6],使得这个方案更像自生成证书方案,而不是基于身份的方案。另外有一些方案[AP03]和[BSN05]提出的CL-PKE用的是安全性较低的Random Oracle模型[1,6]。
最近有学者提出了一种更严格的模型,该模型下的KGC能够在创建体制时在公共参数中留下只有其知道的后门[8]。而且已经有很大一部分CL-PKE加密体制被证明在该模型下是不安全的[1]。所以构造一个在这种模型下安全的加密体制是当前研究的一个热点[9]。本文在标准模型下构建的体制在加密时没有对运算,而且保持了基于身份的特点[10]。
1 基础知识
1.1 对运算
本文中,G1表示一个加群,G2表示一个有着同样阶的乘群,p表示G1的生成元,对运算表示为。对运算有以下一些性质。
(1)双线型性:
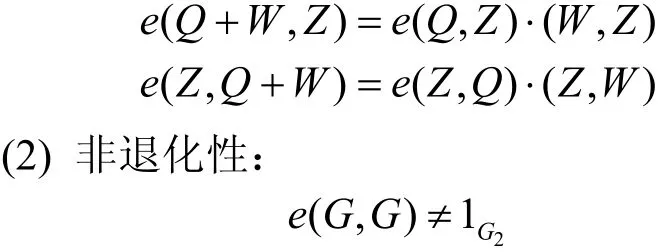
(3)可计算性:对运算是可计算的。
1.2 困难性问题假设
本文使用椭圆曲线上的点构成的对运算的困难性问题假设BDHP(binlineary diffie-hellman problem),定义如下。

式中 A是任意多项式时间的概率算法。
定义 1 如果对于任何多项式时间的概率算法A,都至多有 的优势概率在群G1中解决BDHP困难性问题假设,则BDHP困难性问题假设在群G1中是安全的,表达为:
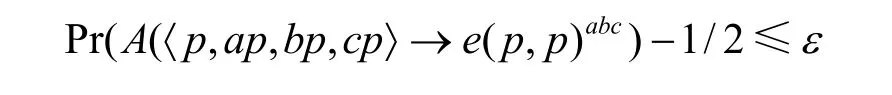
2 算法组成
CL-PKE加密体制有密钥生成中心KGC、系统内用户以及使用系统的外部参与者共3类参与者。最初,文献[1]定义的CP-PKE加密体制由7个算法组成[1],后来被简化成为5个算法[7],分别描述如下。
(1)Setup(K)= ( Params,Master-Key):该算法由KGC执行,目的是由KGC生成密码体制的系统参数和主密钥。算法输入安全参数 K ∈ 1n;输出CL-PKE加密体制的系统参数Params和Master-key。
(2)Partial-Private-Key-Extract (Params,Private-key,ID)=DA:该算法由KGC执行,目的是为每一个系统内的用户生成一个系统范围内的部分私钥。算法输入Params和Master-key以及系统内任意用户的身份ID;输出相应用户的部分私钥DA。通常情况下,该用户的部分私钥DA通过安全的秘密信道交给用户。
(3)Set-User-Key (DA,S,Params)=(Upk,Usk):该算法由系统内用户执行,目的是系统内用户生成一个只有自己知道的用户私钥。算法输入KGC交给用户的部分密钥DA和用户均匀选择的一个随机数S ∈ Z∗p;输出用户的公钥Upk和私钥Usk,其中Upk在系统内公开,Usk由用户秘密保存。
(4)Encrypt(m,Params,ID,s)=C:该算法由系统外任意参与者执行,目的是用相应的系统内用户公钥加密要保密的明文信息m。算法输入要加密的信息m、公共参数Params、用户ID、均匀选择的随机数 S ∈和用户公钥Upk;输出密文C。
(5)Decrypt(C,Usk,Params,ID)=m:该算法由相应的系统内用户执行,目的是用相应的私钥解密密文C。算法输入密文C、用户私钥Usk、公共参数Params和用户ID;输出相应的明文m。
3 安全模型
安全模型可以用一种由两方参与的游戏模拟,一方为攻击者,用A表示,另一方为挑战者,用C表示。在游戏中,攻击者可以向挑战者发出各种不同的Oracle询问,挑战者模拟回答相应的询问。如果挑战者能够正确回答攻击者的各种询问,挑战者就成功模拟了安全模型;而且,如果攻击者赢得了游戏,攻击者就攻破了相应的加密体制[11]。
以下首先对选择性身份模型下CL-PKE的安全模型进行定义,如在引言中所述,CL-PKE加密体制可能遭受到如传统PKE的外部攻击,以及如IBE的内部密钥生成中心KGC的攻击,因此下面针对这两种攻击定义了两种安全模型。
Game 1:外部攻击者和挑战者之间的游戏,攻击者定义为Type1型。
Init:攻击者给挑战者一个要攻击的目标ID∗。
Setup:挑战者根据自己的参数模拟公共参数Params,并把Params交给攻击者。
Phase 1:攻击者可以向挑战者进行Extract Partial Private Key(提取用户的部分密钥)、Extract Private Key(提取用户私钥)、Request Public Key(询问用户公钥)、Replace Public Key(置换公钥)、Decryption Query(解密询问)多项式次询问。挑战者分别进行回答,当攻击者同意时,第一阶段结束。该阶段的目的是让挑战者用模拟得到的公共参数回答攻击者的询问,证明用一定的问题假设模拟的加密体制可以满足攻击者相应的询问。而询问本身就隐含着相应的攻击,为下一步的安全性归约做好了准备。
Challenge:攻击者提供两条明文m1、m2,挑战者均匀选择其中一条加密为Cb,其中b在(1,2)中均匀选择,并交给攻击者,让其辨别是那条明文的加密密文。该阶段的目的是把相应的困难性假设问题归约为辨别密文的困难性。
Phase 2:攻击者继续询问多项式次挑战者在Phase 1中同样的Oracle,并由攻击者决定何时结束。该阶段的目的和第一阶段相似,只是为了使安全模型拥有更高的安全性。
Guess:攻击者输出猜测b′,如果b′=b,那么攻击成功。这一阶段攻击者如果成功那么就辨别了密文,也就解决了相应的难解性问题。然而,实际上难解性问题在当前理论范围内不可解,所以攻击者不可能辨别密文,因而攻击者不可能成功,这就反证了加密体制的安全性。
Type1型攻击者在Phase 1和Phase 2阶段进行询问时,有以下一些限制:
(1)不能询问目标ID∗的用户私钥Usk;
(2)不能询问由目标ID∗加密、要求辨别的加密密文(ID∗, mb);
(3)提交询问密文前,不能置换目标ID∗的用户公钥;
(4)如果询问的加密密文的相应公钥已经被替换过,必须向挑战者提供相应用户私钥中的秘密值。
Game 2:内部攻击者KGC和挑战者之间的游戏,攻击者定义为 T ype2型。该安全模型与Game 1相似。
定义 2 如果任何一个多项式时间攻击者都不能在不可忽略的时间内赢得Game 1(或Game 2),则无证书加密体制(CL-PKE)是 T ype1(或 T ype2)型安全的,CL-PKE加密体制就是IND-CCA安全的。
4 新的CL-PKE加密体制和证明
4.1 新的CL-PKE加密体制
本文介绍的加密体制由5个算法组成,分别定义如下。
Setup:KGC输入参数K,分别输出mpk和msk,mpk由KGC公开,msk由KGC自己秘密保存。其中:


在加密算法中,因为e(g,g)、e(g,h)两个对运算可以提前预计算,所以只需要计算一次就可以被所有用户共享,因而在加密时实际上不需要对运算。
Decrypt:用户输入密文C和自己的私钥,解密如下:

4.2 新的CL-PKE的形式化证明
如果能够用BDHP难解问题的参数模拟新的CL-PKE加密体制的系统参数,并且挑战者可以回答攻击者的相应询问,把难解性问题BDHP归约为辨别密文的困难性,则挑战者模拟成功,新的CL-PKE加密体制符合安全模型的安全性要求。对方案的形式化证明是在攻击者A和挑战者C之间进行的。



5 结 束 语
本文选用自然的困难性假设BDHP构建了加密体制,同时为了获得更好的安全性选用了安全性较高的标准模型,所以本文的基础更加自然,安全性更可靠。如何在保证安全性的前提下提高效率是下一步的工作目标。
[1]Al-RIYAMI S S, PATERSON K. Certificateless public key cryptography[C]//Advances in Cryptology Asiacrypt 2003.Taibei: Springe Verlagr, 2003: 452-473.
[2]GENTRY C. Practical identity-based encryption without random oracle[C]//Advances in Cryptology Eurocrypt 2006.Saint Petersburg: Springe Verlag, 2006: 445-464.
[3]AU M H, CHEN J, LIU J K, et al. Malicious KGC attack in certificateless cryptography[C]//ACM Symposium on Information, Computer and Communications Security 2006.Taibei: ACM Press, 2007.
[4]HUANG Q, WONG D S. Generic certificateless encryption in the standard model[C]//Advances in Information and Computer Security, IWSEC 2007. Nara: Springe Verlag,2007: 278-291.
[5]DENT A W, LIBERT B, PATERSON K G. Certificateless encryption schemes strongly secure in the standard model[C]//11th International Conference on Public Key Cryptography. Barcelona: Springe Verlag , 2007.
[6]ONG H, CHOI K Y, HWANG J Y, et al. Certificateless public key encryption in the selective-ID security model(Without Random Oracles)[C]//Pairing-Based Cryptography-Pairing 2007. Tokyo: Springe Verlag , 2007:60-82.
[7]BAEK J, SAFAVI, NAINI R, SUSILO W. Certificateless public key encryption without pairing[C]//Information Security. Singapore : Springe Verlag , 2005:. 134-148.
[8]CHENG Zhao-hui, CHEN Li-qun, LING Li, et al. General and efficient certificateless public key encryption constructions[C]//Pairing-Based Cryptography-Pairing 2007. Tokyo: Springe Verlag , 2007: 83-107.
[9]WATERS B. Efficient identity-based encryption without random oracles[C]//Advances in Cryptology EUROCRYPT 2005. Aarhus: Springe Verlag, 2005: 114-127.
[10]DENT A W. A survey of certificateless encryption schemes and security models[J]. International Journal of Information Security, 2008,7(5): 349-377.
[11]CHENG Z, COMLEY R. Efficient certificateless public key encryption[R/OL]. [2009-03-14]. http://eprint.iacr.org/2005/012/
编 辑 黄 莘
New Provable Security CL-PKE Encryption Scheme in the Standard Model
YANG Yong and XU Qiu-liang
(Department of Computer Science and Technology, Shandong University Jinan 250010)
A certificateless public key encryption (CL-PKE)algorithm is presented. The proposed CL-PKE algorithm is based on the nature BDHP difficulty assumption and therefore avoids paring computation on elliptic curves, which is the most expensive operation in the encryption algorithm. In CL-PKE algorithm, the selective-ID model is applied instead of the random oracle model. The security and efficiency of the algorithm can be improved compared with some other CL-PKE schemes.
algorithm; BDHP; CL-PKE; public key cryptography; standard model
TP309.7
A
10.3969/j.issn.1001-0548.2010.06.021
2009- 05- 05;
2010- 09- 14
山东省自然科学基金(Y2007G37、2007G10001012);
杨 勇(1980- ),男,博士生,主要从事密码学、信息安全方面的研究.
