小波采样的滤波算法研究
2010-02-08张治国黄建国
张治国,黄建国,刘 震
(电子科技大学自动化工程学院 成都 610054)
小波采样的滤波算法研究
张治国,黄建国,刘 震
(电子科技大学自动化工程学院 成都 610054)
针对经典小波采样理论不能如同香农定理应用采样值对连续信号进行滤波,该文在小波采样存在条件下,提出一种基于采样值的小波滤波算法。该算法突破经典小波采样理论仅研究单个Hilbert空间信号重构的局限性,从多分辨分析逼近出发,基于采样值构建信号逼近准则函数,进而计算信号在小波空间的正交投影,实现小波滤波。仿真试验证明该算法能够有效地基于采样值,对连续信号进行小波滤波。
离散信号处理; 采样理论; 信号滤波; 小波分析
随着计算机和数字化技术的发展,采样理论成为现代信号处理的关键技术和重要基础。目前,实践中普遍采用的 Whittaker-Kotel’nikov-Shannon定理(香农定理)难以处理频域非紧支集(非频段有限)和非均匀采样信号,应用受到极大限制。为解决上述问题,广义采样理论得到迅速发展,其中小波采样理论成为广义采样研究的重要分支[1]。
由于小波采样(基于小波理论实现信号离散化)基于任何L2(R)子空间的理论[2],因此可以有效处理非频段有限采样问题。文献[3-5]分别利用核函数理论,在不同的小波空间中,提出小波采样存在(可以在相应小波空间实现信号离散化)的充要条件。此后,小波采样的非均匀采样[6-7]、平移不变性和多空间理论[8-9]迅速发展,并产生了针对各类特殊小波的采样理论[10-13]。
尽管小波采样理论研究取得了许多重要成果,然而与经典采样理论——香农定理相比,小波采样理论依然有许多值得深入研究的问题,如香农采样的滤波性质。Possion定理说明香农采样等同于信号的低通滤波,因此香农采样不仅可以如同广义采样实现信号重构,而且可以利用采样值,实现信号特征提取和正交分解。该性质与香农函数作为特殊小波父函数,具有多分辨分析性质有密切关系,因此小波采样完全可以具备同样性质。针对上述问题,本文探讨小波采样的多空间性质,提出一种快速计算方法,在小波采样中利用采样值对信号进行小波滤波,实现香农采样的类似性质。
1 小波采样的滤波问题
多分辨分析就是指L2(R)中满足稠密性、平移不变性等 6个性质的一组嵌套空间{Vj}j,其中j∈Z[14]。本文以逼近空间V0中的信号作为讨论的对象,但对于其他多分辨分析逼近空间,本文算法具有相同的有效性。由于香农函数张成的Paley-Wiener空间(P空间)满足多分辨分析条件,因此香农采样本质上是小波采样,使得香农采样与普通小波采样存在许多共性。基于此,本文通过香农采样分析小波采样滤波问题。
设信号fs是P空间V0中的元素,其采样序列表示为:

2 小波采样滤波算法准则函数
尽管基于Possion表达式,香农采样能够实现信号在多分辨分析的正交分解,但对于普通的小波采样,却没有与其相对应的理论,与经典小波采样理论仅从单空间信号重构角度讨论小波采样理论存在密切关系。本文从信号逼近角度出发,基于信号逼近准则函数,获得信号的正交分解量。
2.1 准则函数表达形式


2.2 准则函数合理性分析

因此双无穷矩阵Q是线性有界可逆变换。由式(8)可知, 也是线性有界可逆变换,因此根据Hermitian矩阵性质, 是正定矩阵。证毕。


3 小波采样滤波计算
引理3还证明,信号逼近误差可以通过准则函数转换为采样值误差。基于引理3,定理1将证明,信号在V0子空间上的正交投影是V0子空间Vj中使准则函数减为最小的元素。
基于该重要结论,本文提出相应算法,基于采样值计算信号在Vj上正交分量的级数表达式式(4),实现小波采样滤波。



4 算法仿真试验
4.1 仿真对象
仿真试验选用5阶样条小波多分辨分析作为仿真对象,其对应的小波父函数φ(t)和小波ψ(t)分别如图1a和图1b所示。由G G Walter相关理论可知5阶样条小波多分辨分析存在小波采样,所以可以运用本文的相关算法对信号进行正交分解。

图1 5阶样条小波父函数及小波

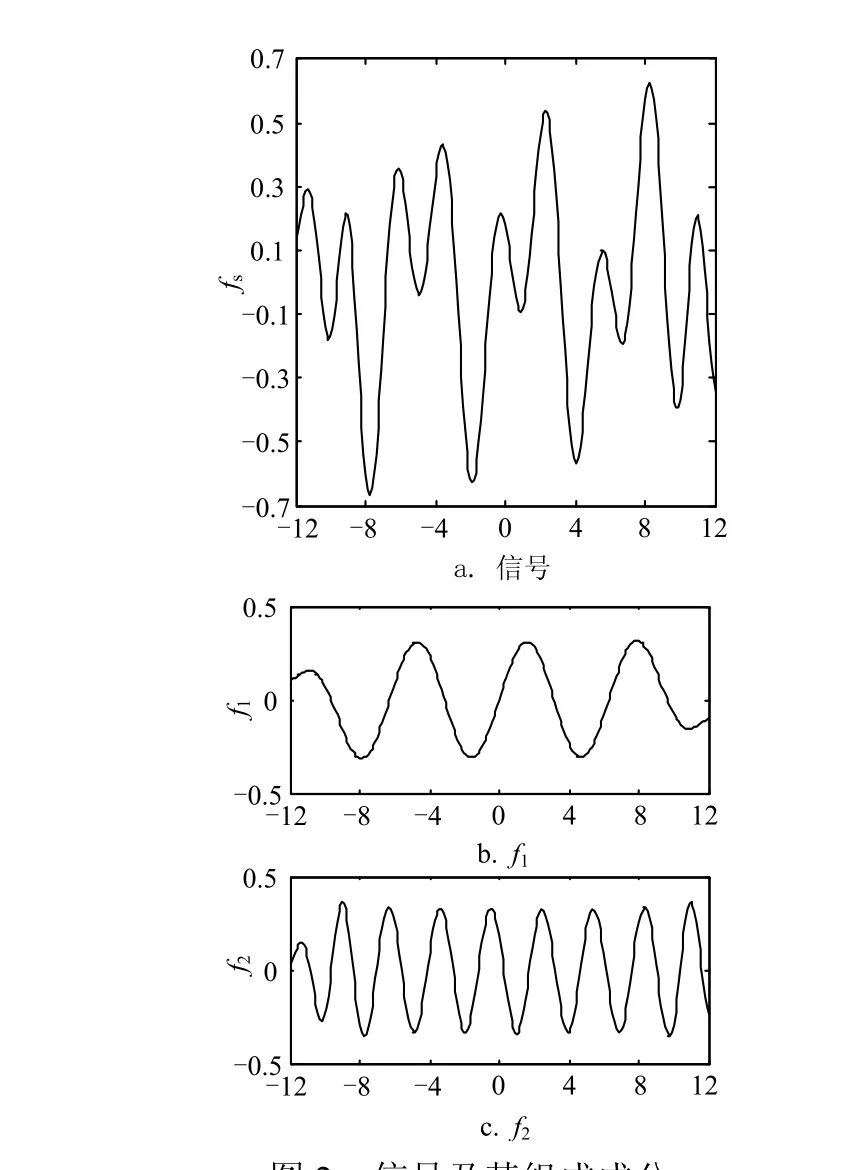
图2 信号及其组成成分
4.2 信号分解仿真结果

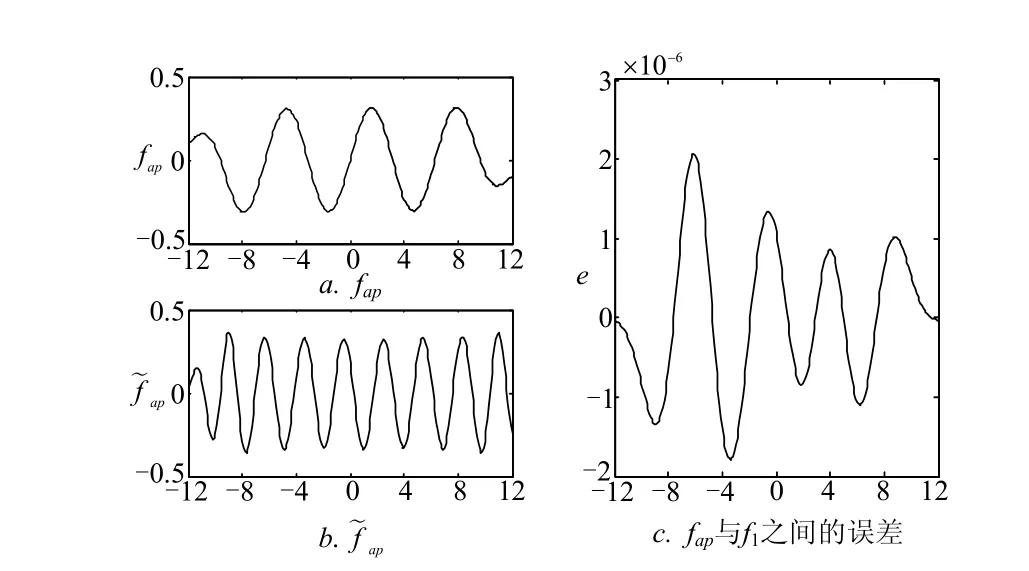
图3 信号分解结果
5 结 论
基于小波采样的存在条件,本文从多分辨分析逼近角度出发,运用插值Riesz基与正交基之间的映射关系,构建小波空间信号逼近准则函数,利用采样值衡量信号逼近误差,进而利用该准则函数提出相应的信号小波正交分解算法,使得小波采样能够如同香农采样那样,进行小波滤波。
由于该算法通过准则函数,间接利用了小波采样的存在性条件和插值Riesz基,因此该算法同样适用于普通的小波和小波父函数基,使该算法与经典小波采样算法相比,具有更大的适用性。
[1]VAIDYANATHAN P P. Generalizations of the sampling theorem: Seven decades after nyquist[J]. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 2001, 48 (9): 1094-1108.
[2]ZHANG Yao. A method to reconstruct nth-order periodically nonuniform sampled[J]. Journal of Electronic Science and Technology, 2006, 2 (2): 15-18.
[3]WALTER G G. sampling theorem for wavelet subspaces[J].IEEE Transaction on Information Theory, 1992, 38(2):881-884.
[4]NAOKI SAITO, BEYLKIN G. Multiresolution representations using the auto-correlation functions of compactly supported wavelets[C]//Proceedings of the International Conference on Wavelets and Applications.Toulouse, France: Frontiesr, 1992: 381-384.
[5]NAOKI SAITO, BEYLKIN G. Multiresolution representations using the autocorrelation functions of compactly supported wavelets[J]. IEEE Transactions on Signal Processing. 1993, 41(12): 3584-3590.
[6]LIU You-ming. Irregular sampling for spline wavelet subspaces[J]. IEEE Transactions on Information Theory.1996, 42(2): 623-627.
[7]CHEN Wen, ITOH Shui-chi. Irregular sampling theorems for wavelet subspaces[J]. IEEE Transaction on Information Theory. 1998, 44 (2): 1131-1142.
[8]WANG Qiao, WU Le-nan. Translation invariance and sampling theorem of wavelet[J]. IEEE Transaction Signal Processing. 2000, 48(5): 1471-1474.
[9]LU Y M, MINH N D. A theory for sampling signals from a union of subspaces[J]. IEEE Transactions on Signal Processing. 2008, 56 (6): 2334-2345.
[10]DEVORE R A, KONGYAGIN S V, TEMLYAKOV V N.Hyperbolic wavelet approximation. Constructive Approximation, 1998, 14: 1-26.
[11]SARDY S, DONALD B P, ANDREW G, et al. Wavelet shrinkage for unequally spaced data[J]. Statistics and Computing. 1999, 9: 65-75.
[12]WANG Jian-zhong. Interpolating cubic spline wavelet packet on arbitrary partitions[J]. Journal of Computational Analysis and Applications. 2003, 5(1): 179-193.
[13]ZHAO Chun, ZHAO Ping. Sampling theorem and irregular sampling theorem for multiwavelet subspaces[J]. IEEE Transactions on Signal Processing. 2005, 53(2I): 705-713.
[14]MALLAT S. A wavelet tour of signal processing[M]. 2nd ed. Beijing: China Machine Press, 2003.
编 辑 张 俊
Wavelet Filtering Algorithm of Wavelet Sampling
ZHANG Zhi-guo, HUANG Jian-guo, and LIU Zhen
(School of Automation Engineering, University of Electronic Science and Technology of China Chengdu 610054)
A new algorithm of wavelet sampling is proposed since the typical wavelet sampling lacks the capacity to filter the continuous signal by the samples as Shannon sampling does. From the viewpoint of Multiresolution approximation, a new cost function based on the samples is introduced to estimate the approximation of signal in this algorithm, so that the signal is decomposed into the orthogonal components, which has break through the limit of typical wavelet sampling that only considers the construction of signal in one Hilbert space.
discrete signal processing; sampling theorem; signal filtering; wavelet analysis
TP301.6
A
10.3969/j.issn.1001-0548.2010.05.020
2009- 04- 08;
2010- 01- 29
国家自然科学基金(60474069)
张治国(1977- ),男,博士,高级工程师,主要从事小波采样及系统仿真方面的研究.
