起落架磁流变减振系统的特性分析研究

黄 琦，李华琳，陈 勇，李 坚

(电子科技大学自动化工程学院 成都 611731)

起落架磁流变减振系统的特性分析研究

黄 琦，李华琳，陈 勇，李 坚

(电子科技大学自动化工程学院 成都 611731)

大型飞机的安全研究，起落架是保障飞机起飞与降落安全的关键部件，该文根据起落架的减振系统对其进行动力学特性分析。由于磁流变阻尼力的出现，导致了起落架磁流变减振系统成为了非线性系统，为了研究系统特性，通过对其非线性部分线性化，构造出起落架磁流变减振系统的动力学数学模型，分析不同阻尼比下机身位移、机身加速度、起落架位移和起落架动载荷的频率响应，并对跑道的随机路面激励时域特性分析，这对起落架磁流变减振系统结构设计和减振系统优化控制具有重要意义。

频域响应; 起落架; 磁流变减振系统; 时域分析

飞机起飞和降落时会受到地面巨大的冲击力，为了减少路面冲击对飞机造成的不良振动，起落架上安装了减振的装置，小型飞机用弹簧减振，大型飞机则用液压减振器减振。但是现在飞机安全事故中，因起落架故障造成的事故占相当比例，因此，急需一种新型智能减振器可调节、自适应地缓解路面的冲击力。

近年来，磁流变减振器已经成为国内外的研究热点[1-5]，磁流变减振器可以根据路面作用力的大小和飞机的运动状态，在毫秒级的时间内自适应改变减振器参数使其性能达到最优。目前，磁流变减振器已经应用到了高端车上，如凯迪拉克的赛威和奥迪的“TT”跑车等，但飞机上的应用我国还处于空白。国内有中国民航大学、西北工业大学、重庆大学等，对磁流变减振器进行了一些磁流体特性分析。磁流变减振器在起落架中的推广和应用需要解决的关键技术就是减振器的结构设计、控制策略两部分，这两个关键技术是建立在起落架磁流变减振系统特性分析基础上的。

因此，本文在起落架的动力学特性基础上建立起落架磁流变减振系统的非线性数学模型，并对其进行线性化，分析不同阻尼比下机身位移、机身加速度、起落架位移和起落架轮子动载荷的频率响应，并对跑道的随机路面激励时域特性进行分析，为起落架磁流变减振系统的结构设计和优化控制提供依据。

1 起落架磁流变减振系统动力学分析

在起落架的动力学特性基础上建立的起落架磁流变减振系统的非线性数学模型[6-8]如图1所示，其中Mu是机身质量，Md是起落架质量，Ks为弹簧刚度，Kt为起落架轮子刚度，Xu为机身垂直位移，Xd为起落架垂直位移，Xr为跑道路面输入垂直位移，C0是零磁场磁流体的粘滞系数。

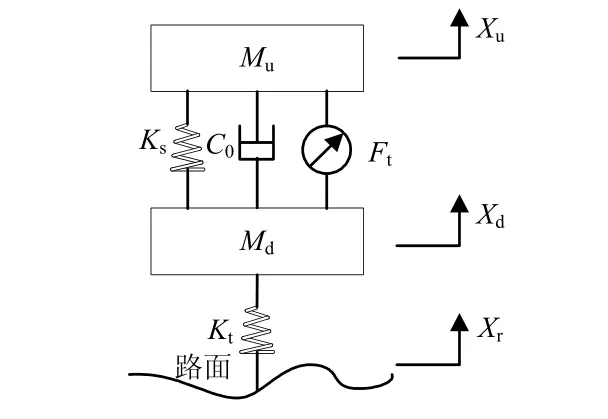
图1 起落架磁流变减振系统

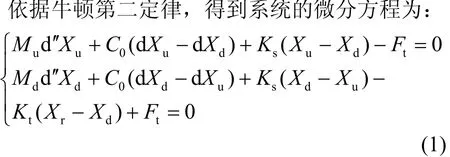
起落架磁流变减振系统通过改变减振器的阻尼系数产生相应的可调阻尼力Ft，它是非线性的，其非线性的影响主要是由于磁流变液在外加磁场下的非线性、回滞性和饱和性引起的。为了能够使减振器的可调范围大，往往选择性能优越的磁流变液，尽可能使磁流变减振器工作范围在磁流变液的线性区间。

通过实验分析，可调阻尼力Ft与磁流变液的励磁电流i之间的函数关系为：

式中 Ct为磁流变液粘滞系数，由磁流变液的励磁电流来调节，其变化能够有效地反映磁流变液阻尼力的变化。

将磁流变减振器的可调阻尼力Ft分段线性化：

当Ct=0时，模型为一般起落架的力学模型，将其代入式(1)，得：

通过对起落架磁流变减振器的可调阻尼力线性化，得到相对于路面激励的机身位移、机身加速度，起落架位移和起落架动载荷的传递函数，为分析不同阻尼比下起落架减振器的特性提供了方便，同时也有利于磁流变起落架控制策略的优化。

2 起落架磁流变减振系统的频率响应分析

考虑式(5)系统的传递函数，略去阻尼和外加激励，得到系统的无阻尼微分方程为：

依据起落架磁流变减振系统的传递函数，通过设置系统不同的阻尼比，利用Matlab仿真得到机身位移、机身加速度、起落架动位移和起落架轮子动载荷在不同阻尼比下的幅频特性曲线，如图2所示。

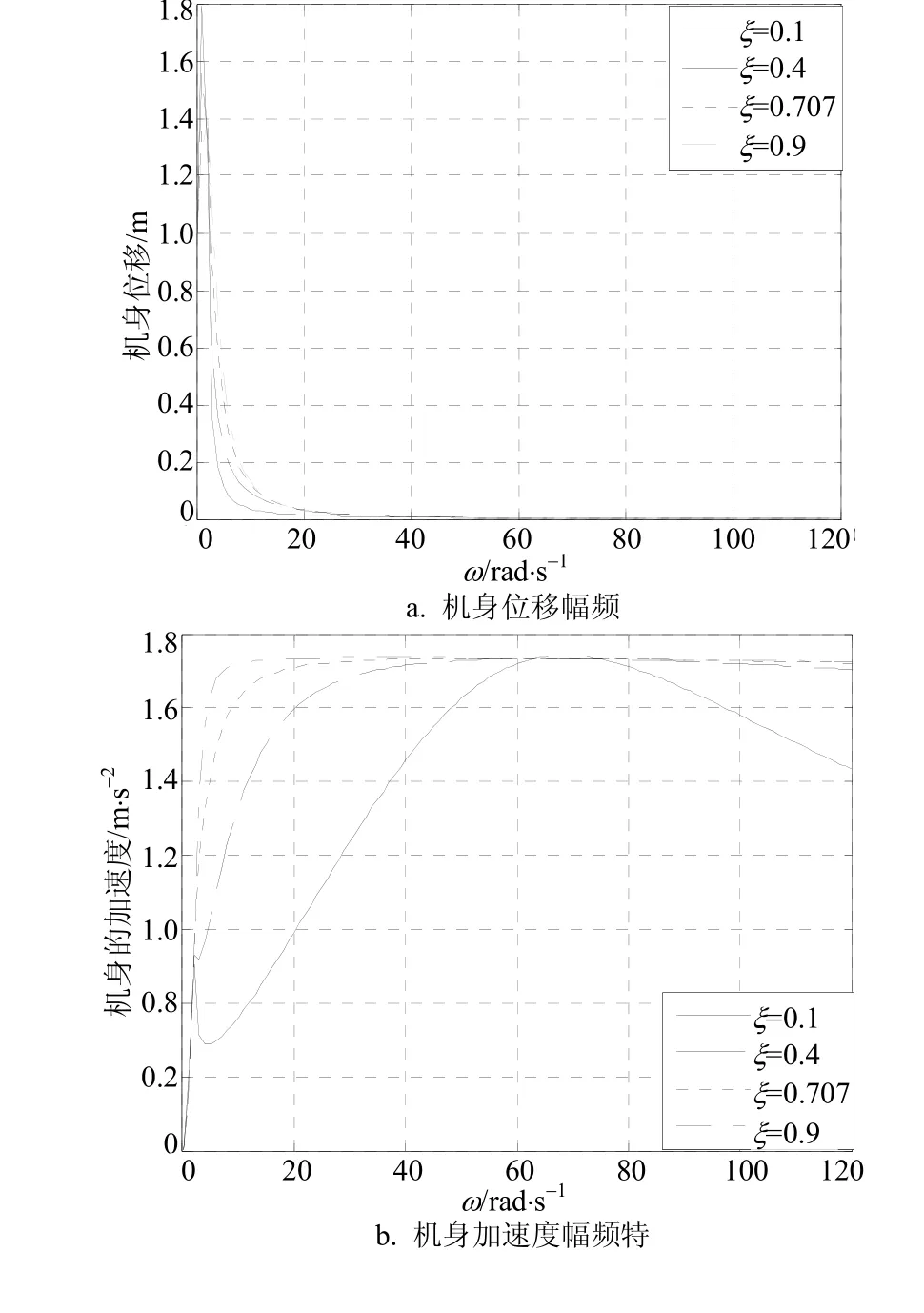
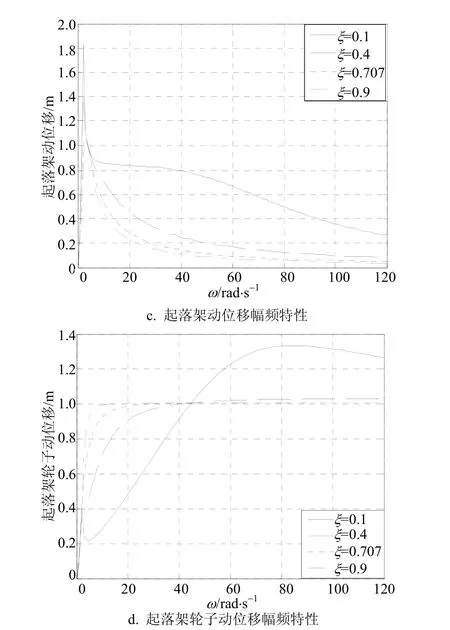
图2 起落架的幅频特性

由图2可以看出，在阻尼比ξ=0.1时波形的两个尖峰，即为起落架减振系统的两个固有共振频率，因此，将横坐标按照其固有的共振频率分为低频段(0到第一共振频率)、中频段(第一共振频率与第二共振频率之间)和高频段(大于第二共振频率)。从图2a可以看出，在系统低频段，随着起落架减振系统阻尼比的增大，机身位移迅速减小；而在中高频段，随着阻尼比的变化，机身位移变化不大，且随着频率的增大，机身位移逐渐减小，在第二共振频率处不出现波峰，机身位移比较平稳，趋近于零。从图2b可以看出，在低频段，随着阻尼比的增大，机身加速度减小；在中频段和高频段，随着阻尼比的增大，机身加速度增大，机身加速度变化量不大，加速度基值较大；在第二共振频率处，且阻尼比ξ=0.1时，有个尖峰，随着路面输入频率的增大而减小并趋于稳定。从图2c可以看出，在整个频段内，起落架动位移随着阻尼比的增大而减小，尤其是在低频段起落架动位移减小很明显。从图2d可以看出，在低频段，随着阻尼比的增大，起落架轮子动位移减小；在中频段，随着阻尼比的增大，起落架轮子动位移增大；在高频段，随着阻尼比的增大，起落架轮子动位移减小程度变缓。

由此可知，在低频段，机身位移、机身加速度、起落架动位移和起落架轮子动位移都随着阻尼比的增大而减小，因此，在低频段应设置较大的阻尼比。在中频段，由于机身的加速度和起落架的动位移随着阻尼比的增大而增大，考虑到中频段是人体的敏感频段，应设置小的阻尼比以提高飞机的舒适性和安全性。在高频段，机身加速度随着阻尼比的增大而增大，起落架的动位移随着阻尼比的增大而减小，因此，高频段阻尼比的设定由具体情况而定，考虑乘坐的舒适性要求，应设置小的阻尼，考虑操纵的稳定性要求，应设置较大的阻尼比。

3 跑道随机路面激励时域特性分析

3.1 跑道路面输入仿真

跑道路面输入大致可以划分为随机路面和冲击路面两类[9-10]。随机路面是指沿道路方向的连续激励。对于连续型随机路面，一般采用空间频率功率谱密度函数以及相应的时域表示形式加以描述。冲击路面是指在较短时间内的离散事件，并且有较高的强度，如平坦道路上的凸包和凹坑。一般采用脉冲信号、阶跃信号和半波正弦信号进行描述，把测量得到的随机数据Xr，经数据处理得到路面功率谱密度[11-13]，本文采用滤波白噪声作为随机路面的输入模型，其数学模型为：

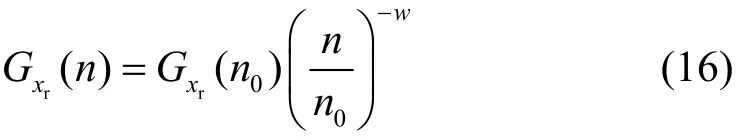
0xr0平度系数；w为频率指数，确定每段功率谱斜线的斜率，取值由路面谱的频率结构确定，分级路面谱的频率指数w=2。

为了分析研究起落架时域的动态特性，需要进一步把频域内的统计特性转变为时域内的时间序列。于是路面轮廓可以由功率谱密度为的白噪声通过一个积分器产生，建立其Simulink仿真模型，如图3所示。

图3 随机路面的输入仿真

xr 0 72 m/s，其生成的随机路面轮廓如图4所示：

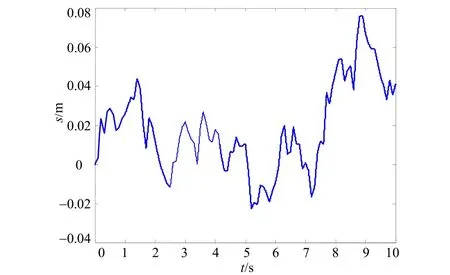
图4 随机路面输入的时域模型仿真

3.2 起落架系统仿真

利用起落架动力学微分方程和随机路面输入模型建立仿真模型如图5所示。

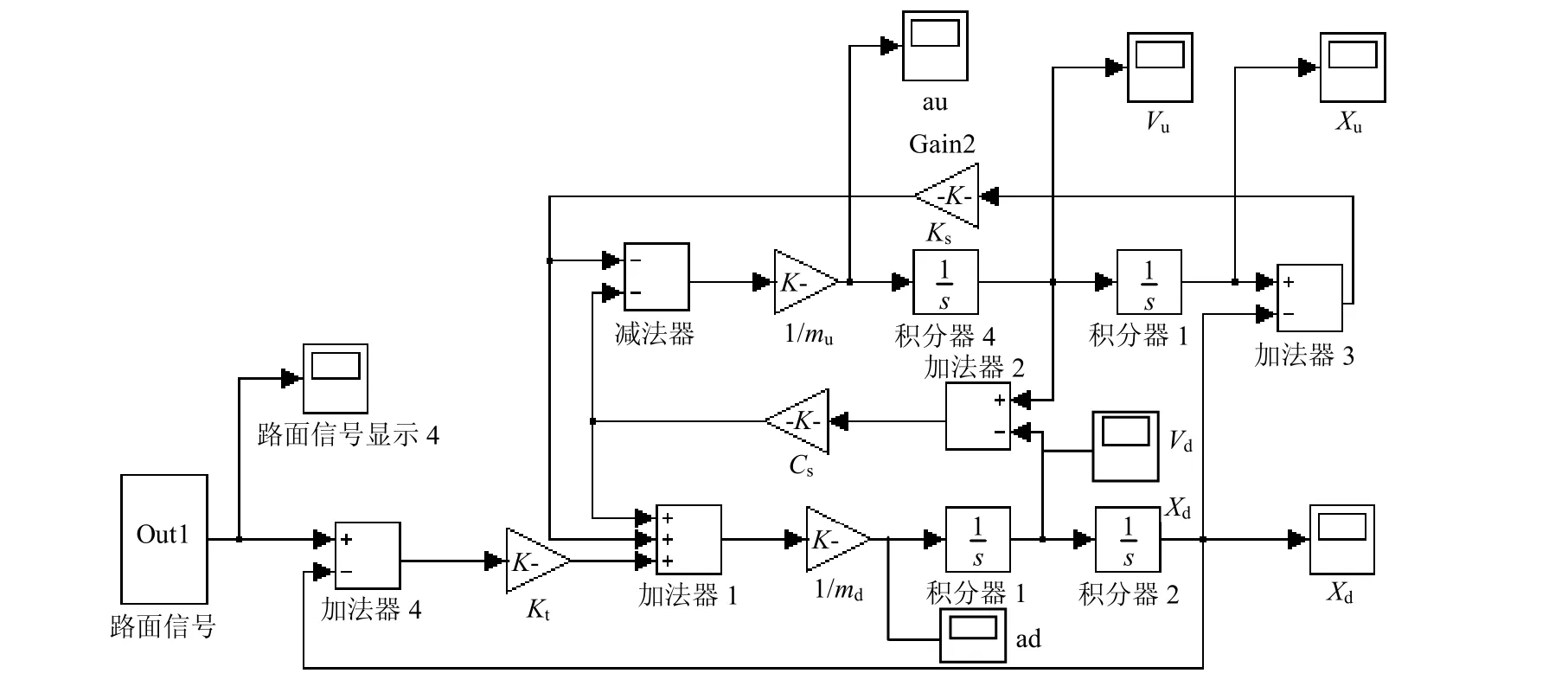
图5 起落架系统仿真模型

考虑到人体对飞机着陆过程的平顺性和舒适 性，最主要是通过感觉机身振动的频率和强度评价的。参考C级路面，飞机着陆后某一时刻速度为72 m/s，通过改变起落架的阻尼参数，得到系统不同阻尼比下机身振动的加速度如图6所示。

从图6可以看出，在C级路面，飞机速度为72 m/s时，调节起落架的阻尼比，得到起落架阻尼比在ξ=0.1时，机身的加速度幅值最小，证明此时机身的平顺性和舒适性最好。通过调节不同的路面输入激励和系统不同的阻尼比能够得到不同级别路面的最佳阻尼比，从而为起落架磁流变减振系统的结构设计和优化控制提供依据。

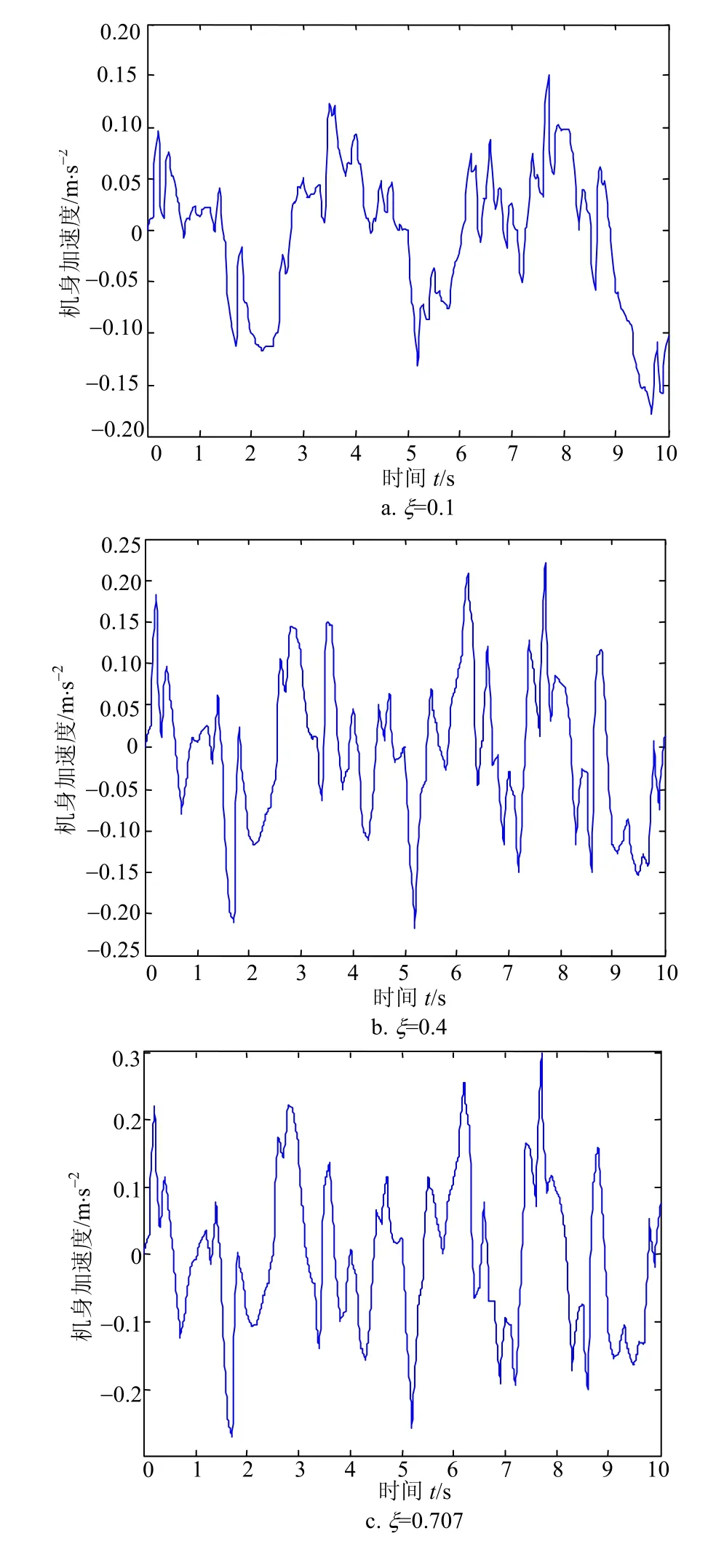
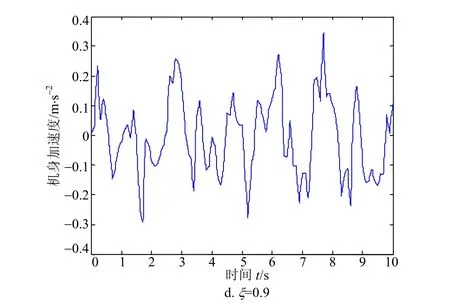
图6 不同阻尼比下的机身加速度

4 总 结

本文从起落架的动力学特性分析出发，分析不同阻尼比下机身位移、机身加速度、起落架动位移和起落架轮子动位移的幅频特性，建立了随机路面输入的时域模型和起落架减振器模型，并在一定速度下，得到不同阻尼比下机身加速度的时域特性。

针对起落架减振器的固有共振频率，详细分析了不同频段改变系统的阻尼比对起落架减振器特性的影响，针对不同的路面激励，通过可调阻尼力得到最优的阻尼比，兼顾飞机操纵稳定性和舒适性，提高飞机的安全性。

[1]徐冬苓, 李玉忍. 飞机起落架数学模型的研究[J]. 系统仿真学报, 2005, 17(4): 831-833.

XU Dong-ling, LI Yu-ren. Mathematical model research on aircraft landing gear[J]. Journal of System Simulation, 2005,17(4): 831-833.

[2]CHOI Young-tai, WERELEY N M. Vibration control of a landing gears ystem featuring[J]. Journal of Aircraft, 2003,40(3): 432-439.

[3]CARLSO J D, CATANZARITE D M, St CLAIR K A.Commerctal Agneto-Rhellogical Fluid Devices[C]//Proceedings of the 5th International Conference on ER Fluids, MR Suspensions and Associated Technology.Singapore: [s.n.], 1996.

[4]CARLSO J D, CATANZARITE D M, St CLAIR K A.Commercial magnetorheological fluid devices[J].International Journal of Modern Physics B, 1996, 10,(23-24): 2857-2865.

[5]RAKHBA S, HONG S, SANKAR T S. Analysis of a passive sequential hydraulic damper for vehicle suspension[J]. VSD,1990, 19: 289-312.

[6]CHOI S B, LEE H S, HONG S R, et al. Control and response characteristics of a magneto-theological fluid for passenger vehieles[J]. SPIE, 2000, 3985: 438-433.

[7]WENTSCHER H. Design and analysis of semi-active landing gears for transport[J]. Aircraft, 1996, (1): 134-157.

[8]赵 亮, 文桂林, 韩 旭, 等. 基于磁流变阻尼器的车辆半主动悬架最优控制的研究[J]. 汽车工程, 2008, (4):340-344.

ZHAO Liang, WEN Gui-lin, HAN Xu, et al. An investigation into the optimal control of vehicle semi-active suspension based on magnetorheological damper[J].Automotive Engineering, 2008, (4): 340-344.

[9]檀润华, 陈 鹰, 路甬祥. 路面对汽车激励的时域模型建立及计算机仿真[J]. 中国公路学报, 1998, 6(3): 96-102.

TAN Run-hua, CHEN Ying, LU Yong-xiang. The mathematical models in time domain for the road disterbances and the simulation[J]. China Journal of Highway and Transport, 1998, 6(3): 96-102.

[10]BURTON A W. Apractical application of MATLAB:Automotive semi-active suspension design[J]. IEE Control Engineering, 1993, 48: 23-43.

[11]何亚东, 黄金枝. 智能磁流变(MR)阻尼器半主动控制的研究.振动工程学报[J]. 2003, 16(2): 198-202.

HE Ya-dong, HUANG Jin-zhi. Study on structural intelligent semi-active control based on MR damper[J].Journal of Vibration Engineering, 2003, 16(2): 198-202.

[12]SHEPHERD A, CATT T, COWLING D. The Simulation of aircraft landing gear dynamics[C]//ICAS, Congress, 18th.Beijing, China: [s.n.], 1992: 1317-1327.

[13]YANG Guang-qiang. Large-scale magneto-theological fluid damper for vibration mitigation: Modeling testing and control[D]. Indian a: University of Notre Dame, 2001.

编 辑 漆 蓉

Analysis of the Characteristics of Landing Gear with MR Fluid Damper System

HUANG Qi, LI Hua-lin, CHEN Yong, and LI Jian

(School of Automation Engineering, University of Electronic Science and Technology of China Chengdu 611731)

Landing gear of aircraft is the key component to ensure safety during the process of takeoff and landing. This paper analyzes the dynamic characteristics of the landing gear system. Because of the inclusion of MR fluid, the landing gear damper system becomes a nonlinear system. In order to study the characteristics of the system, this paper builds the mathematical model of the landing gear damper by linearizing the nonlinear system.Based on the model, the frequency response of aircraft body displacement, aircraft body acceleration, landing gear displacement, and tire dynamic loading of the landing gear are analyzed. And the time-domain response of random road excitations is also analyzed. These analyses would be helpful in structure designing of the landing gear with MR damper and the advanced control of the damper system.

frequency response; landing gear; MR fluid damper system; time domain analysis

TP13; TH703.6

A

10.3969/j.issn.1001-0548.2010.06.014

2009- 06- 04;

2009- 10- 14

教育部博士点专项基金(200806141056)；四川省应用基础研究项目(2009JY0008); 四川省青年基金(09ZQ026-009)

黄 琦(1976- )，男，博士，教授，博士生导师，主要从事分布式检测技术、电力系统方面的研究.