中国宏观经济总量波动趋势检验——基于结构突变单位根理论的分析

任燕燕 袁丽娜

一、问题的提出

单位根理论的最主要的意义在于如果一个经济时间序列是含有单位根的,那么它的趋势是随机的,由随机信息累加得到。每一个随机信息对该序列的未来运动方向都具有持续的影响。即现实生活当中任何冲击对经济体系的影响都将是持久的,短时间之内不能得以消除。而如果经济时间序列不含单位根,则它的趋势沿着确定性均衡路线上下随机波动,外界的冲击只是对经济发展的局部产生短暂性影响,并不能对经济发展的长期均衡路径产生持久性冲击。不同的结论对政府政策主导下的宏观调控有着重要影响。因此,对经济时间序列的研究和应用首先要确定其是否含有单位根。

但是,常规的单位根检验方法如ADF检验法、PP检验法等,并没有考虑经济时间序列受到重大冲击发生结构突变的情况。目前,有关含有结构突变的单位根检验的研究属于新兴领域,尤其是国内的研究和应用甚少。

二、国内外相关文献综述

1.国外理论研究综述

Nelson&Plosser(1982)①Nelson,C.R.,and Plosser,C.,“Trends and Random Walks inMacroeconomic Time Series:Some Evidence and Implications”,Journal ofM onetary Econom ics,1982(10):139-162.是较早对宏观经济序列到底是带有趋势的平稳波动序列还是不带确定性趋势的非平稳序列进行研究的学者之一。他们分析了美国 14个宏观经济变量,检验结果认为除了失业率序列之外其他 13个宏观经济序列都属于差分平稳过程,这也就意味着对于大多数的宏观经济总量而言,当前的冲击对其长期水平具有持久性的影响。

通过对美国经济发展史的深入研究,Perron(1989)①Perron,P.,“The great crash,the oil price shock,and the unit root hypothesis”,Econometrica,1989(57):1361-1401.认为 1929年的经济大萧条和 1973年的石油价格危机对经济总量产生了巨大影响。因此,他将上述事件作为结构突变点纳入单位根检验体系,并建立了一个相对完备的理论体系,从而成为结构突变单位根检验的里程碑。Perron(1989)对Nelson&Plosser(1982)中的数据进行了再次检验,认为绝大多数的宏观经济时间序列数据并不具有单位根,在允许 1929年的截距变化和 1973年后的斜率变化的情况下,绝大多数的宏观经济时间序列数据是分段趋势平稳的。

考虑到 Perron(1989)将结构突变看作是外生的局限性,Zivot&Andrew(1992)②Zivot,E.,and Andrews,D.,“Further Evidence on the Great Crash,the Oil-Price Shock,and the Unit-Root Hypothesis”,Journal ofBusiness and Economic Statistics,1992(10):251-270.将 Perron(1989)有条件的单位根检验扩展为无条件的单位根检验,再次检验了 Perron(1989)的样本数据集,结果显示:如果采用渐进分布得到的临界值,那么在 5%的显著性水平上,Perron(1989)所认为的可以拒绝单位根假设的 10个序列中有 4个序列是无法拒绝零假设的,而且在 5%或者 10%的显著性水平上无法拒绝战后真实 GNP季度序列是含有单位根的;而如果采用有限样本分布得到的临界值,那么在 5%的显著性水平上无法拒绝另外3个总量是含有单位根的③该结论也称为“逆 Perron现象”。。

同时对结构突变点的外生假设提出质疑的还有 Christiano(1992)④Christiano,L.,“Searching for a Break in GNP”,Journal of Business and Econom ic Statistics,1992(10):237-250.和 Banerjee、Lumsdaine&Stock (1992)⑤Banerjee,A.,Lumsdaine,R.,and Stock,J.,“Recursive and Sequential Testsof theUnit-Root and Trend-Break Hypotheses:Theory and International Evidence”,Journal of Business and Econom ic Statistics,1992(10):271-287.。Perron也意识到外生性假设的局限性,与 Vogelsang一起于 1992年⑥Perron,P.,and Vogelsan,T.,“Nonstationarity and Level Shiftswith an Application to Purchasing Power Parity”,Journal of Business and Econom ic Statistics,1992(10):301-320.放弃了之前的外生性假设,对所有可能的结构突变点进行检验,认为美国和英国、美国和荷兰之间的真实汇率是含有截距突变的平稳序列。但是,即使是采用结构突变点内生决定的方式,Perron(1997)对 1989年研究中的宏观经济序列进行二次验证,结果仍然支持当初的结论,他指出对数据处理方式、模型选择以及滞后阶数确定的差异是造成结果偏差的主要原因。

鉴于无法证明只包含一个结构突变点是否是宏观经济总量动态特征的最好描述,Lumsdaine&Papell (1997)⑦Lumsdaine,R.,Papell,D.,“Multiple Trend Breaks and the Unit-RootHypothesis”,The Review of Econom ics and Statistics,1999(79):212-218.将 Zivot&Andrew(1992)的方法延伸到了考虑两个结构突变点。结果发现,与 Zivot&Andrew (1992)的结论相比,更多的总量是分段趋势平稳的,但其数量要少于 Perron(1989)的结果。Lumsdaine& Papell(1997)与 Zivot&Andrew(1992)研究结果的差异说明了结构突变点的个数对宏观经济总量动态特征的验证结果有一定干扰性。

Sen(2000)⑧Sen,A.,“OnUnitRoot TestsWhen TheAlternative Is a Trend-Break Stationary Process”,working paper,Departmentof Economics,University of M issouri-Rolla,2000(21):1-45.指出如果检验模型中突变形式的设定与实际的数据生成过程不吻合,就会导致模型检验功效的严重损失。故其建议在实际应用过程中要遵循从一般到特殊的原则进行试验,最终确定结构突变的形式。

2.国内理论研究综述

研究中国宏观经济总量动态特征的文章一般都是采用传统的单位根检验,结果认为总量变量是 I(1)或者差分平稳的。考虑到中国经济在新中国成立之后经历了众多大的变革,因此在总量上存在结构变化的可能性很大。

Xiao-MingLi(2000,2005)对中国宏观经济总量的结构变化进行了一系列研究。Li(2000)⑨Li,X.M.,“The GreatLeap Forward,Economic Reform,and theUnitRootHypothesis:Testing forBreaking Trend Functions in China’s GDPData”,Journal of Comparative Econom ics,2000(28):814-827.利用中国1952-1998年的样本数据对真实 GDP和第一、二、三产业的真实产出等四个序列进行了分析。在不考虑结构突变点时,检验结果显示上述四个序列都是含有单位根的,第一、二、三产业的总产出对数序列是差分平稳的即 I(1),而 GDP是具有非线性时间趋势的随机游走过程。这与大多数没有考虑结构突变点的文献分析结果是吻合的。但是考虑新中国成立以来历史的巨大波动,忽略结构突变点是不合理的,因此他根据历史事件对经济趋势的改变程度,选择了带有两个结构突变点的模型进行分析,认为上述四个序列是分段趋势平稳过程而不存在单位根。Li(2005)①Li,X.M.,“China’s Economic Growth:What doWe Learn from Multiple-break Unit Root Tests”,Scottish Journal of Political Economy,2005 (52):261-281.又对中国 1952-2002年间第三产业总产出和第二、三产业的职工人均产出的动态特征进行了研究,结果显示在考虑三个结构突变点的情况下所有的总量都是分段趋势平稳的。

Smyth&Inder(2004)②Smyth,R.,and InderB.,“Is Chinese Provincial Real GDP per capita Non-stationary?Evidence from Multiple Trend Break Unit Root Tests”, China Econom ic Review,2004(15):1-24.指出 Li(2000)所采用的 t统计量是 Perron(1997)只考虑一个结构突变点时的临界值,但是模型却是含有两个突变点的,并不匹配。他们对中国 1952-1998年间 25个省、自治区和直辖市年度人均真实 GDP进行了研究。他们首先对样本期间的人均真实 GDP进行了没有结构突变点和含一个结构突变点的分析,ADF检验结果显示大约有四分之三的省份的人均真实 GDP是含有单位根的。ADF、PP、ERS(Elliot、Rothenberg&Stock,1996)检验结果显示在含有一个结构突变点的情况下,25个省份中85%以上是具有单位根的。在考虑两个结构突变点时,当两个结构突变点同时出现在趋势方程的斜率和截距项上时比结构突变点仅出现在趋势方程的截距项上时,单位根假设被拒绝的可能性增大。但是总体来说,在考虑两个结构突变点时,大约有一半省份的人均真实 GDP序列是分段趋势平稳的。

在Li(2000,2005)、Smyth&Inder(2004)的研究基础上,梁琪、滕建州 (2006a)③梁琪、滕建州:《中国宏观经济和金融总量结构变化及因果关系研究》,《经济研究》2006年第 1期。对包括反映总产出、生产要素、总需求和金融发展等在内的10个中国宏观经济和金融总量的动态特征进行了研究,并且在研究结果的基础上对分段趋势平稳的总量进行了消除趋势的处理,存在两个结构突变点的模型回归结果表明 10个经济变量中有 6个是分段趋势平稳的。采用Lee&Strazicich(1999,2004)所提出的最小LM单位根检验方法,梁琪、滕建州(2006b)④梁琪、滕建州:《我国总产出的动态特征研究——基于最小拉格朗日乘数单位根检验的实证分析》,《数量经济技术经济研究》2006年第 6期。再次验证了我国名义 GDP、实际 GDP和实际人均 GDP是分段趋势平稳过程。

栾惠德、张晓峒(2006)⑤栾惠德、张晓峒:《中国人口时间序列的单位根检验:基于结构突变理论》,《经济学报》2006年第 2期。通过蒙特卡罗模拟讨论了含有两次内生结构突变点的单位根检验模型的设定问题,并运用这一模型对我国人口时间序列进行了检验,得出结论认为其服从含有两次结构突变点的趋势平稳过程。

三、我国宏观经济总量波动趋势的实证检验

1.变量的选择、样本区间和数据处理

为了探讨中国宏观经济总量的动态特征,本文选取了名义 GDP、真实 GDP、第一、二、三产业的总产值、名义工资、实际工资、就业、消费者物价指数、金融机构存款总额、贷款总额、固定投资、最终消费、进出口总额和外汇储备等涵盖经济发展各方面的 15个指标进行验证,同时考虑到人均经济变量中要使用人口总数进行平减,故本文也将全国总人口纳入验证的指标范围内。各宏观变量数据分别来源于《新中国五十年统计资料汇编》、2000-2007年各年《中国统计年鉴》。其中,除了进出口总额序列时间跨度为 1950-2006年,全国总人口时间跨度为 1949-2006年,其余序列的时间跨度均为 1952-2004年。除外汇储备序列⑥我国外汇储备在 1980年曾为负值。之外所有序列取自然对数。真实 GDP是名义 GDP经过平减之后得到的。真实 GDP即名义 GDP除以 1952年为基期的 GDP消减指数后的结果。第一、二、三产业的总产值源于三大产业名义产出总量。名义工资源于全国职工工资总额。实际工资是以 1952年为基期的消费者价格指数对名义工资进行价格平减之后得到的。就业源于全国就业人员。消费者物价指数是对以 1950年为基期的指数的调整,最终确定为 1952年为基期,反映了 1952年以来物价水平的总体变动。金融机构存款总额和贷款总额在一定程度上反映我国金融发展的整体水平。固定投资、最终消费、进出口总额和外汇储备均取名义量进行验证。

2.不含结构突变点的单位根检验

在进行含有结构突变的单位根检验之前,必须首先验证宏观经济总量在整体样本区间上不含结构突变点时的平稳性。

本文采用ADF检验、KPSS检验、PP检验以及 ERS检验的两种方法DF-GLS检验和 PT检验对上述16个宏观变量进行常规单位根检验。在这 5种方法中,KPSS检验的零假设为被检验序列是趋势平稳变量,其余 4种方法的零假设均为被检验序列是含有单位根的非平稳时间序列。本文取 pmax=10。使用 Eviews 5.0软件,基于 t-sig方法①t-sig方法的核心思想是对滞后阶数 p的选取依据 t统计量的显著性。即保证检验式中最后一个自回归滞后项系数的 t统计量是显著的。选择检验式中的差分滞后阶数 p。对检验式(1)的检验结果见表 1。

其中:△yt=yt-yt-1为变量 yt的一阶差分,

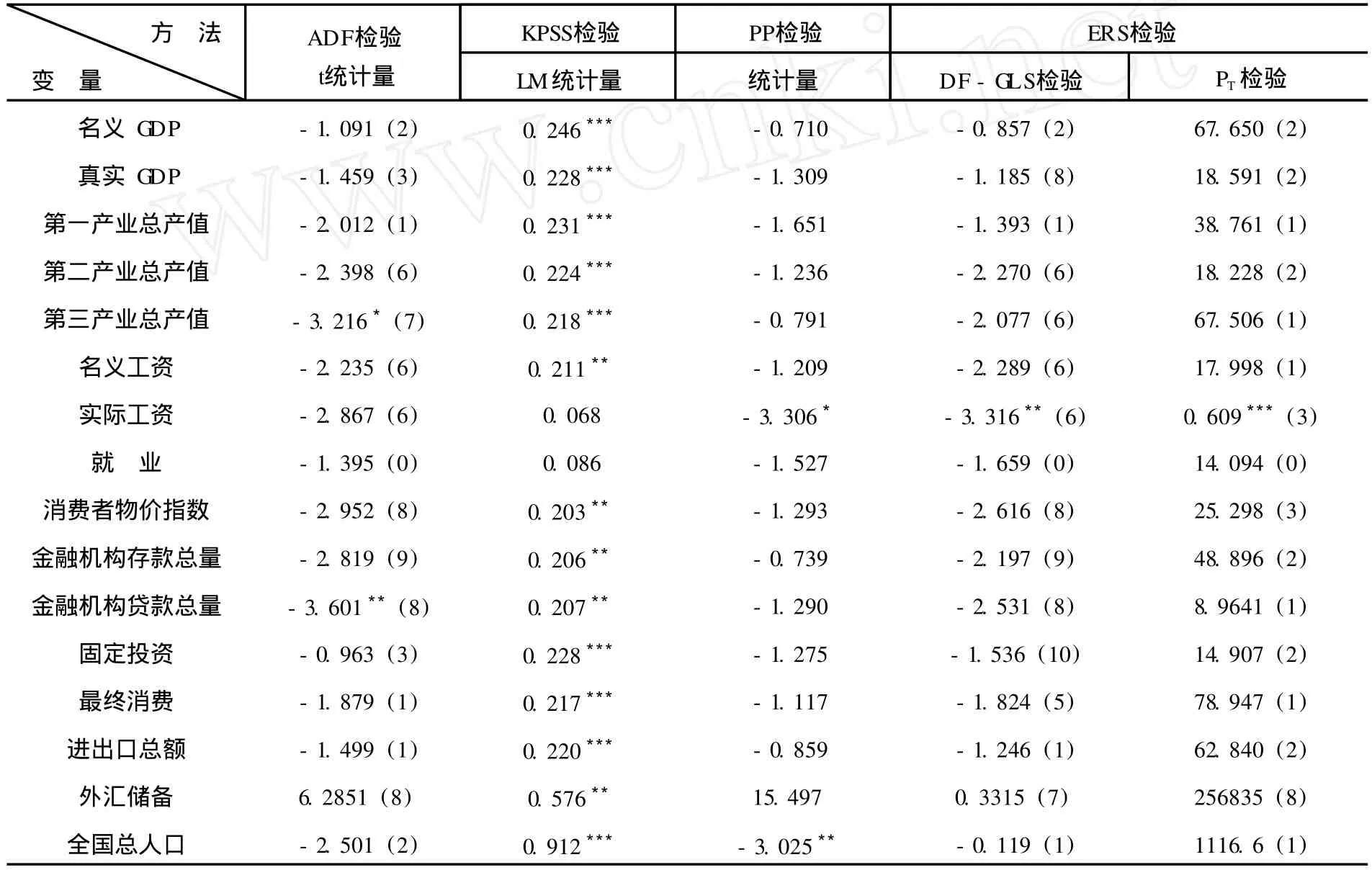
表1 不含结构突变点的单位根检验结果

由表 1的检验结果看出,对于名义 GDP、真实 GDP、第一、二产业总产值、名义工资、消费者物价指数、金融机构存款总量、固定投资、最终消费、进出口总额、外汇储备和全国总人口这 14个序列来说,无论是ADF检验结果还是 KPSS、PP、ERS检验结果均显示它们是具有单位根的非平稳序列。但第三产业总产值、实际工资、就业、金融机构贷款总量这 4个变量的ADF、KPSS、PP、ERS检验结果并不完全吻合。ADF检验结果显示,序列第三产业总产值和金融机构贷款总量分别在 10%和 5%的显著性水平下拒绝单位根假设,而 KPSS、PP、ERS检验结果认为这 2个序列是含有单位根。就业在 KPSS检验中接受了原假设,认为序列本身是平稳的,但是其它 4种检验均推翻了 KPSS检验的认知。基于此,我们仍旧将第三产业总产量、就业和金融机构贷款总量作为非平稳序列进行更深入的研究。但是对于实际工资序列 KPSS、PP、DF-GLS和PT检验等四种方法都拒绝了单位根假设,故认为该序列本身是平稳的,不再进行含有结构突变的单位根检验。

3.含有一个结构突变点的单位根检验

在不含结构突变点的单位根检验过程中,如果检验结果拒绝单位根过程,则可认为该序列是平稳序列;但若是非平稳的,则还不能得出最终结论,因为检验研究的假设前提是序列的数据生成过程是无结构变化的。而在现实情况中,由于受到剧烈的外生冲击都可能导致序列的数据生成过程的结构突变。如果在检验过程中不考虑这种突变,直接采用单位根检验,则会把一个带有水平突变或者趋势突变的退势平稳过程误判为随机趋势平稳过程,造成“伪单位根”。因此,需要对不含结构突变点的单位根检验过程中接受单位根结论的序列进行进一步的加入结构突变点的单位根验证。

中国经济在新中国成立之后经历了诸多变革,因此在总量上存在结构变化的可能性很大。在将经济中的结构变化看作是内生,并允许一个结构突变点的情况下,本文采用 Zivot&Andrew(1992)的三模型来研究中国宏观总量的波动特征。

按照从一般到特殊的模型选择原则,首先使用 Zivot&Andrew(1992)的模型 C进行检验。如果检验式中表示截距突变和斜率突变的虚拟变量系数均显著,则表明模型 C是合适的检验模型,不再使用模型A或模型B检验;如果检验式中表示截距突变或者斜率突变的某个虚拟变量系数不显著,则对其进行剔除,只保留显著变量进行模型A(如果斜率虚拟变量不显著)或模型B(如果截距虚拟变量不显著)检验。

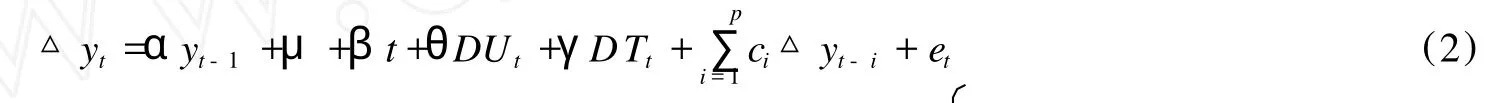
首先,模型 C检验式如下: TB是结构突变发生的年份;变量DUt是表示截距突变的虚拟变量;变量 DTt是表示斜率突变的虚拟变量其中即原假设为序列是非平稳的,备择假设为序列是一个以 TB时刻为分界点的分段平稳过程。

本文采用 t-min统计量方法①t-min统计量方法检验功效高,对突变点的判断简单准确,是目前国际理论界使用频率较高的方法。来确定结构突变点,通过使用 Eviews 5.0编程,对(2)式在区间 (0.15T, 0.85T)内进行迭代回归,序列中最小值对应的年份 TB为结构突变点出现的时间。模型 C检验结果如表2所示。

表 2 含有一个结构突变点的模型 C单位根检验结果

注:(1)p表示滞后阶数,根据 t-sig方法确定;(2)＊＊＊、＊＊、＊分别表示在 1%、5%、10%的显著水平上拒绝原假设;(3)下同。

模型 C检验结果显示第三产业总产值、名义工资、就业、消费者物价指数、进出口总额和全国总人口等6个序列中变量DU和DT的系数均显著,说明这 6个序列是适合采用该模型的。其中名义工资和就业 2个序列在 1%的显著水平上拒绝单位根零假设,意味着这 2个序列是含有 1个结构突变点的分段趋势平稳过程。而第三产业总产值、消费者物价指数、进出口总额和全国总人口 4个序列在加入结构突变点之后依旧拒绝单位根零假设,即含有一个结构突变点的单位根检验结果显示这 4个变量是非平稳的。

表 2检验结果显示采用模型 C检验的真实 GDP序列中表示斜率突变的虚拟变量DT系数不显著,表示截距突变的虚拟变量DU系数则在 1%的显著水平下显著,因此需要剔除斜率突变因素,只采用含有截距突变点的模型A检验。模型A检验式如式(3)所示。

TB是结构突变发生的年份;变量 DUt是表示截距突变的虚拟变量,其中,使用 Eviews 5.0编程对真实 GDP序列进行模型A检验,结果如表 3所示。

表 3 含有一个结构突变点的模型 A单位根检验结果

含有一个截距突变点的单位根检验结果表明真实 GDP序列在 1%的显著水平上拒绝单位根假设,即结果显示该序列是分段趋势平稳的。真实 GDP序列在结构突变点 1960年附近有较大跳跃,但是增长速度并没有改变。

表 2检验结果显示采用模型 C检验的名义 GDP、第一二产业总产值、金融机构存贷款总量、固定投资、最终消费和外汇储备等 8个序列中表示截距突变的虚拟变量DU系数不显著,而表示斜率突变的虚拟变量DT系数在至多是 10%的显著水平下显著,因此需要剔除截距突变因素,只采用含有斜率突变点的模型 B检验。模型B检验式如式(4)所示。TB是结构突变发生的年份;变量 DUt是表示斜率突变的虚拟变量,其中,使用 Eviews 5.0编程对上述 8个序列进行模型B检验,结果如表 4所示。

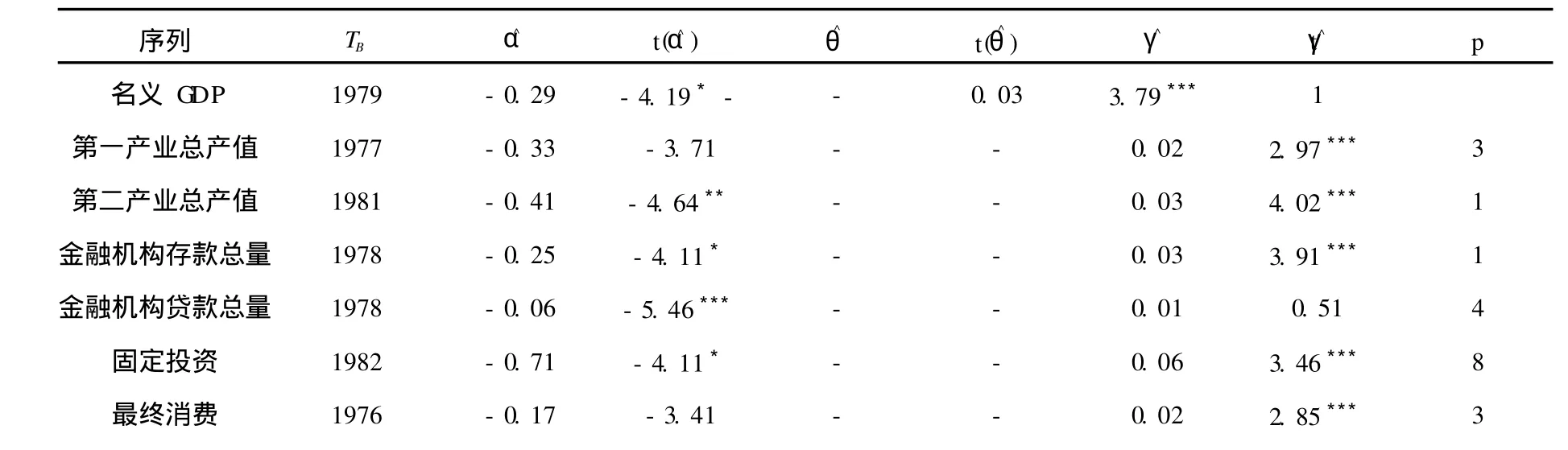
表 4 含有一个结构突变点的模型 B单位根检验结果

外汇储备 1998 0.25 0.27 - - 124.97 0.93 8

由表 4含有一个斜率突变点的单位根检验结果可以看出名义 GDP、第二产业总产值、金融机构存款总量和固定投资 4个序列分别在 10%、5%、10%和 10%的显著水平上拒绝单位根假设,同时 DT系数显著。金融机构贷款总量虽然在 1%的显著水平上拒绝单位根假设,但是DT系数并不显著。其他 3个序列如第一产业总产值、最终消费和外汇储备并不能拒绝单位根假设,因此含有一个结构突变点的单位根检验表明这 3个序列仍旧是非平稳的。

四、我国宏观经济总量波动趋势分析

对表 2到表 4检验结果的汇总分析如表 5所示。通过加入一个结构突变点的单位根检验模型验证表明,在常规单位根检验情况下均呈现非平稳状态的 15个宏观序列,在加入一个结构突变点时只有 7个序列仍旧接受单位根假设,有 8个序列被证明是分段趋势平稳过程。

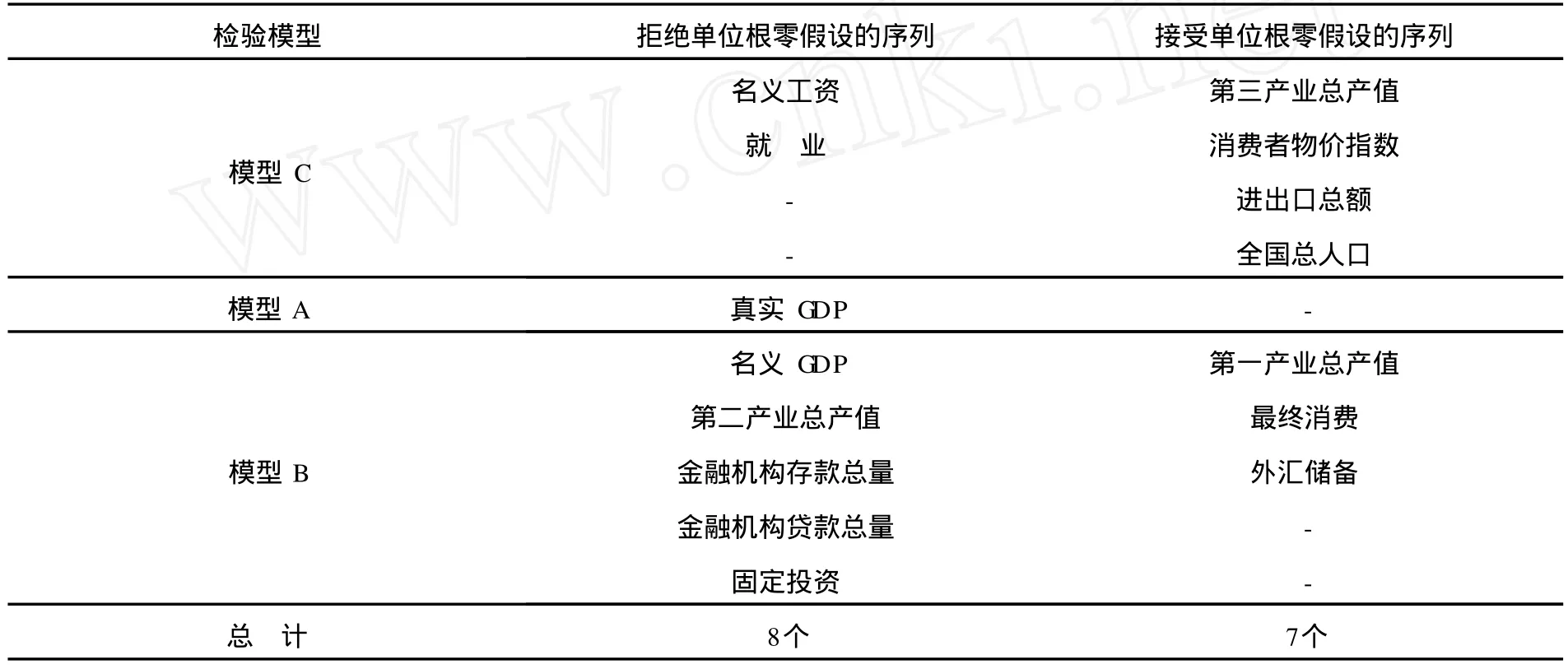
表5 模型A、B、C检验结果汇总

其中,在加入一个结构突变点时拒绝单位根原假设的 8个序列的检验参数详见表 6。

表6 分段趋势平稳序列检验结果汇总

含有一个结构突变单位根检验结果显示表 6所示 8个序列的长期增长路径是固定的,只有少数足够大的冲击才能够改变其长期增长趋势。对于这些序列来说,其波动是围绕长期增长路径的上下浮动,在结构突变出现之前,序列的波动不会过大的偏离长期增长路径。

对于名义工资序列来说,结构突变发生在 1983年,说明改革开放四年的积累对名义工资的长期增长路径产生了正向效应。对于就业来说,结构突变的时间出现在 1989年,结构突变截距虚拟变量系数为正,斜率突变虚拟变量系数为负。通过对原始数据的观察,发现就业在 1989年出现截距突变的原因是第一产业就业人员的快速增长,第一产业就业人员在样本期内的平均增长率是 1.53%,但是在 1989-1990年间增长率高达 17.3%。而就业量增长速度的减小则归咎于工种和工种需求量的稳定。剔除 GDP的消胀因素之后,真实 GDP序列的结构突变发生在 1960年,且截距突变虚拟变量为负,说明 1958-1959年的大跃进对我国经济产生了直接的负面影响,使得真实 GDP较之前有明显下降,但是大跃进只是显著的减少了我国真实GDP的存量,对其增长速度并没有产生实质性的影响。对于名义 GDP序列而言,1979年改革开放的作用要大于大跃进的影响。改革开放对名义 GDP的显著影响在于加速了名义 GDP的增长速度,使其在现有存量的基础上迅猛增长。第二产业总产值和固定投资序列的结构突变点分别出现在 1981和 1982年,结构突变虚拟变量系数均为正,说明经过 1979年改革开放的积累和助力,二者的增长速度均有所提高。对于金融机构存款总量和贷款总量两个序列来说,它们的结构突变点都发生在 1978年,斜率突变虚拟变量系数分别为 0.03和 0.01,说明文革的结束和即将开始的改革开放对银行存贷款产生了长期的正面影响。

本文确定的结构突变时刻主要有三个:1960年、1979年前后和 1989年,其中结构突变点发生在 1979年前后的有名义工资、名义 GDP、第二产业总产值、金融机构存款和贷款总量以及固定投资等 6个序列,而且这 6个序列在检验过程中的结构突变虚拟变量系数均为正。这说明 1979年的改革开放是我国经济发展史上的重大举措,对我国宏观经济起到了举足轻重的促进作用。改革开放的开始改变了我国部分宏观经济总量的长期发展路径。

宏观经济总量是分段趋势平稳还是单位根过程的结论有着重要意义。一方面,如果宏观经济序列是含有单位根的非平稳过程,那么序列是围绕一个随机趋势波动的,外在的任何冲击都可以改变总量的长期增长路径;另一方面,序列到底是具有单位根的还是分段趋势平稳的结论对研究宏观经济总量之间相互关系具有重大的影响。