时间和价格影响需求的变质物品促销研究
2010-02-06姚卫坤合肥工业大学管理学院安徽合肥230009
姚卫坤 (合肥工业大学 管理学院,安徽 合肥 230009)
0 引 言
从20世纪60年代起,许多学者开始关注变质物品的研究,Hadley&Whitin[1]是最早考虑到库存会发生腐蚀现象的学者。Dave和Patel[2-3]考虑需求随时间线性递增以及商品腐蚀的特性,进而求得固定订购周期与不允许缺贷时的最佳订购批量。Wee[4]提出 “允许部分补货”的观念,他将缺货期间的补货率假设为0-1之间的固定常数,考虑变质物品在生命周期处于衰退期的库存模型。Chakrabarti和Chaudhuri[5]则提出在SFI定购策略下,考虑需求随时间呈指数递减的变质物品的库存模型。
但是有关变质物品的研究中考虑数量折扣的模型还不是很多见,Wee[6]在购买价格不变的前提下,讨论了需求随价格和时间变化的条件下零售商在一定计划期内各周期的最优库存策略。Wee和yu[7]注意到数量折扣对零售商库存策略的影响,讨论了供应商给予暂时折扣时零售商的库存策略,但是假定需求在整个计划期内是不变的。Monahan[8]首次从供应商的角度研究了数量折扣的问题。L[9]等考虑了一个供应商和多个零售商的数量折扣问题,并给出了供应商给予数量折扣的一个算法。
而对于临时价格折扣的研究,大多是研究零售商在面对供应商的优惠政策时如何订货和定价,Tersine[10]首先研究了临时价格折扣,并提出了OTOS(one time only sale),随后他和Price[11]、Ardalan[12]讨沦了没有供应商特别订货量限制的临时价格折扣的存贮模型,然后Tersine[13]提出了一个基于临时价格折扣的一般化EOQ模型。
然而上面关于临时价格折扣的研究都是假设供应商提供价格折扣,然后零售商决定最优订货量或者最优订购周期。而本文是从零售商的角度出发,考虑临时价格折扣的制定问题,研究的是零售商做出的面向顾客的临时价格折扣,这在现实中也是零售商经常采用的一种促销手段,尤其是在销售变质物品时。文章通过建立相应的数学模型及对其求解,决策出零售商应该在什么时候给多大的折扣价格,使得他的利润会最大,即决策变量是折扣开始时间和临时价格折扣系数,决策条件是利润最大。同时文章也考虑了零售商做出价格折扣决策后对需求的影响,所以本文所开展的研究有一定的现实意义。
1 符号说明及假定
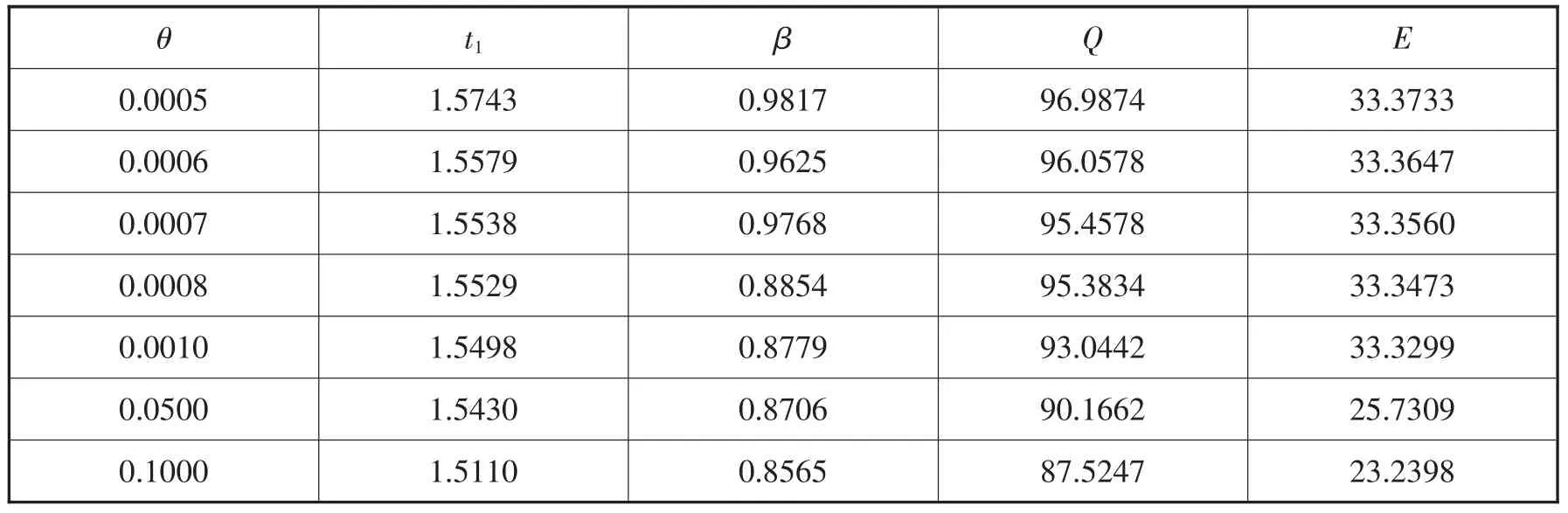
为了便于建立模型,本文给出以下假定: (1)只考虑一个销售周期; (2)不允许缺货,周期结束时,库存为零; (3)物品变质不是从入库开始,而是有一个拖后时间td,且0 模型中的符号含义:T——销售周期长度I(t)——物品在t时刻的库存水平h——单位时间单位物品的库存费用p0—— 零售商每单位物品的购买价格p——零售商每单位物品的售价,p>p0D(t)——物品在t时刻的需求率,且D(t)=(a-bt) p-k,a>0,b>0,k为常数 β——临时价格折扣系数,为决策变量,且0<β<1 t1——零售商采取临时折扣开始时间,为决策变量,且0<t1<Tθ——物品的变质率,为常数E——零售商单位时间内的平均总利润HR——一个周期内零售商的销售收入HY——一个周期内零售商的库存成本HC——一个周期内零售商的购买成本A——零售商每订购一次物品的固定订购成本 由模型假设可以知道,物品在0≤t1≤t时间段,需求函数为: 从t1时刻开始由于实施价格折扣策略,且折扣系数为β,所以在t1≤t≤T时间段,需求函数为: 因为变质不是从入库开始的,而是有一个拖后时间td,所以零售商库存的减少在变质之前是由于销售影响,在变质之后是由于销售和变质同时影响,同时在t1时刻零售商实施了价格折扣策略,由此零售商的库存水平是分为三阶段的,下面分A,B两种情况讨论: A.当0<td<t1时, 可以知道库存水平分三种情况, 即在0≤t≤td为I1(t ), 在 td≤t≤t1为 I2(t ), 在 t1≤t≤T为I3(t), 并且可知道库存水平的变化率为: 所以,由 (9)、 (10)、 (11)可得零售商在单位时间内的平均总利润=(销售收入-库存成本-购买成本-固定订货成本,即: 对于A种情况,所建立的模型是关于β和t1的二元函数,通过求偏导可以解出β和t1,进而求出零售商的最大平均利润,即: 把 (21)式代入 (19)式中,可以得到一个关于t1的一元方程,进而可以解出t1,再把t1代入 (21)式,就可以解出β,最后把β和t1代入 (12)式中就可以求出零售商的最大平均利润。 对于B种情况,可以用同样的方法求出解。 然后对不同的物品开始变质时间td,可以分别代入 (12), (18)式求出最优策略,在从它们两个结果中选择出零售商利润最大的一个策略,即为模型的最优解。 在具体求解模型的过程中,可以通过常用的数学软件matlab优化工具箱求出最优解。 为了说明模型的实用性,下面给出应用例子。 (1)假设a=100,b=10,T=5,p=4,p0=2,k=1,h=0.05,A=10,td=0(即物品的变质从入库开始),当物品变质率不同时,通过matlab计算可以得到表1中的数值计算结果。 表1 变质率不同时对利润的影响分析 从表1中可以看出,若物品变质从入库开始,当物品变质率增大时,实施折扣的时间越要提前,折扣系数也越来越小。而当物品变质率接近时,零售商的平均利润也很接近,但是当变质率忽然变大时,零售商的平均利润也会减少很多,可见变质率对折扣开始时间,临时折扣系数和利润的影响是非常显著的。在实际问题中,也往往是物品越容易变质,零售商越担心变质影响销售,也越会提早采取折扣,这和计算结果相符合。从表中也可以看出,当物品变质率变化时,零售商的订货量基本不变,从而可以说明零售商在适当的时间给合适的折扣价格是很又必要的。当θ=0.0005时,E=33.3733,当θ=0.1时,E=23.2398,平均利润减少了33.36%。 (2)假设a=100,θ=0.05,T=5,p=4,p0=2,k=1,h=0.05,A=10,当物品的变质开始时间不同时 (即td不同时),可以得到表2是数值计算结果。 表2 变质开始时间不同对利润的影响分析 从表2中可以看到,当物品变质开始时间越来越晚时,即物品越不容易变质,临时折扣开始的时间也就越来越晚,这和实际很相符合。而对于不同的变质开始时间,代入模型中通过分析比较可以决策出最优的促销策略,所以零售商在适当的时候打折扣对其利润是有一定影响的,这从表中可以很明显的看出。 本文分析了需求随时间和价格变化条件下,零售商在销售易变质物品时面向顾客做出的临时价格折扣,决策变量是临时折扣系数和折扣开始时间,决策条件是零售商的利润最大化,通过本模型零售商可以决策出折扣开始时间和临时折扣价格。其实还可以结合变质物品的质量状况,考虑多个折扣开始时间和折扣系数,使得零售商的平均利润最大。其中,发生价格折扣的时间及多大的折扣价格对需求变化都有一定的影响。本文研究中的一些不足: (1)我们只是从零售商的角度考虑,如果能从整个供应链的角度出发,设计出一个临时折扣价格和折扣开始时间的模型,使得整个供应链的利润最大,同时零售商的利润也达到最大。 (2)本文考虑的是一个销售周期,实际上还可以考虑有限计划期内多个销售周期的情况,在此情况下零售商的最大利润模型应该如何确定?这些问题均有待进一步研究。 [1] Whitin T M.The theory of inventory management[M].Princeton:Princeton University Press,NJ,1957:34-55. [2] Perry D.A double band control policy of a Brownian perishable inventory system[J].Probability in Engineering and Informational Science,1987,11:361-373. [3] Dave Pate1.Financila firms risk losing business in race to comply with new mortgage regulations[J].Computer Weekly,2003,38:162-188. [4] Wee H M.Economic production lot size for deteriorating taking account of the value of money[J].Computers&Operations Research,2000,26:545-558. [5] Giri B C,Chaudhuri K S.Heuristic models for deteriorating items with shortages and varying demand and costs[J].International Journal of Systems Science,1999,28:153-159. [6] Wee H M.Joint pricing and replenishment policy for deteriorating inventory with dechning market[J].International Journal of Production and Economics,1995,40:163-171. [7] Wee H M,Yu J.A deterioration inventory model with a temporary price discount[J].International Journal of Production E-conoimcs,1997,53:81-87. [8]Monahan P.A quantity pricing model to increase vendor profits[J].Management Science,1984,30(6):1398-1400. [9]Lee H L,Rosenblatt M J.A generalized quantity discount pricing model to increase supplier's profits[J].Management Science,1986,32(9):1177-1185. [10] Lal R,Staelin R.An approach for developing an optimal discounts pricing policy[J].Management Science,1984,30(12):1524-1539. [11] Tersine R J,Grasso E T.Forward buying in response to announced price increases[J].Journal of Purchasing and Materials Management,1978,14(2):20-22. [12] Tersine R J,Price R L.Temporary price discounts and EOQ[J].Journal of Purchasing and Material Management,1981,17(4):23-27. [13] Ardalan A.Option Policies in Response to sale[J].Lie Transactions,1988,20(3):292-294. [14] Tersine R J,Barman Samir.Economic purchasing strategies for temporary price discounts[J].European Journal of Operational Research,1995,80(2):328-343.2 模型的建立


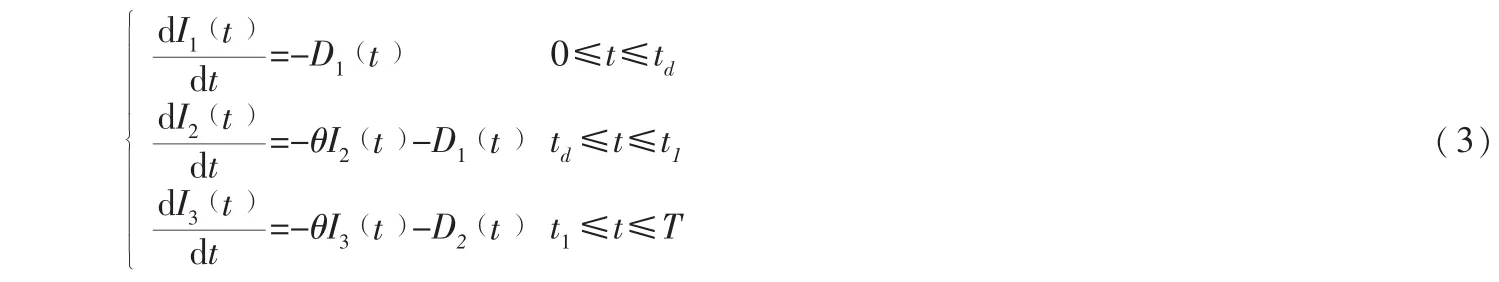


3 模型求解

4 算例分析

5 结束语
