高分子基导电复合材料非线性导电行为及其机理(Ⅱ)量子力学隧道效应理论
2010-01-30梁基照杨铨铨
梁基照,杨铨铨
(华南理工大学工业装备与控制工程学院,广东广州510640)
0 前言
将导电填料加入到绝缘的高分子基体中,然后采用物理或化学方法复合后,就得到了高分子基导电复合材料。高分子基导电复合材料既具有导电功能,同时也具有类似于高分子材料的优异的力学和加工性能[1]。高分子基导电复合材料通常呈现非线性导电行为。其电导率随导电填料的体积分数增加而增大,当达到某一临界值时,在一个很窄的体积分数范围内,由绝缘体变成导体,通常称此为逾渗转变,导电填料的临界体积分数称为复合材料的逾渗阈值[2]。
描述高分子基导电复合材料的非线性导电行为的理论目前主要有:导电通道理论[3-13]和量子力学电子隧穿理论[14-16]等。导电通道理论认为:电子可沿着相互接触的粒子进行传递而使体系导电。但是,当复合体系中导电填料的体积分数较低、导电粒子间距较大(大于1 nm)时,复合导电体系中依然存在导电现象。很显然,这不是靠导电粒子的接触来实现的,导电通道学说无法解释该现象,只有用隧道效应理论才能较合理地解释。
本文重点讨论描述高分子基导电复合材料非线性导电行为的隧道效应理论。
1 量子力学隧道效应理论
隧道效应理论是应用量子力学的结果。量子力学电子隧穿学说认为:由于微观粒子具有波动性,即使电子不具有足够的能量从势垒顶部翻越过势垒,它们仍然能够在势垒的一边消失,而在势垒的另一边出现[17],因而可以在相互靠近但并不接触的导电粒子之间进行传递,使体系导电,且导电电流,即:隧穿电流是导电粒子间间隙宽度的指数函数。隧道效应几乎仅发生在距离很接近的导电粒子之间,间隙太大的导电粒子之间没有电流产生。
在二元组分导电复合材料中,当高电导率组分的体积分数较低(在逾渗阈值附近)时,隧道导电效应对材料的导电行为影响较大。
Polley等人[18]通过研究后发现:碳黑填充橡胶的复合体系在碳黑尚未成链或橡胶在延伸状态下也有导电现象发生。他们研究了电阻率与导电粒子间隙的关系,发现在导电粒子间隙较大时也存在导电现象,认为这是电子隧穿的结果。Polley因此提出了“并不是因为成链,而是由于电子在势垒间隧穿而导通”的理论。他假设导电粒子在基体中均匀分布,得到以下公式:
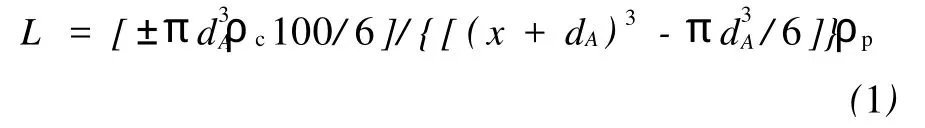
式中:dA=6/Aρc;L为碳黑的体积分数,%;A为碳黑粒子的比表面积,m2/g;dA为碳黑粒子的直径, nm;x为碳黑粒子的间距,nm;ρc,ρp分别为碳黑粒子和基体树脂的密度 ,g/cm3。据此,罗延龄[19]等人求得两种碳黑的体积分数为15%~30%时的粒子间距x,如表1所示。

表1 不同碳黑的体积分数的碳黑粒子间距Tab.1 The distance between carbon black particles indifferent volume fraction of carbon black
由该模型求得的碳黑粒子间平均距离在1.5 nm以上。这与导电通道理论认为的碳黑粒子在1 nm以内才能导电的结论相背。这只有用隧道效应理论才能作出合理的解释。
Voet[20]也认为:复合材料导电虽然与导电网络形成有关,但不是靠导电粒子直接接触来导电;而是热起伏时电子在粒子间跃迁所造成的。其间隙在10 nm以上(远比1 nm大)。并给出以下关系式:

式中:j(ε)是导电粒子间隙的电场强度为ε、间隙当量电导率为 j0时的隧穿电流;W为间隙宽度;|ε| <ε0;X=(4πmV0/h2)1/2(式中:m为一个电子的质量,h为普朗克常数,V0为间隙势垒);e0= 4V0/em(e为一个电子的电量)。
由方程(2)可见:隧穿电流是间隙宽度的指数函数,随着间隙宽度的增加,隧穿电流迅速下降。两相邻导电粒子发生隧道效应的平均间隙宽度为[21]:S=2(3N/4π)1/3,式中:N为单位体积的导电粒子数目。
Sheng等人[15]提出的热波动诱导隧穿机理认为:如果间隙中热起伏所产生的电场为eT,且外加电场eA<|eT|时,则实际的隧穿电流

并进而推得低电压下
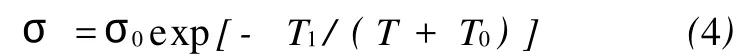
其中:
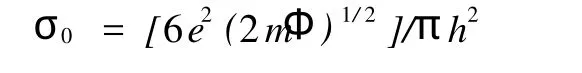

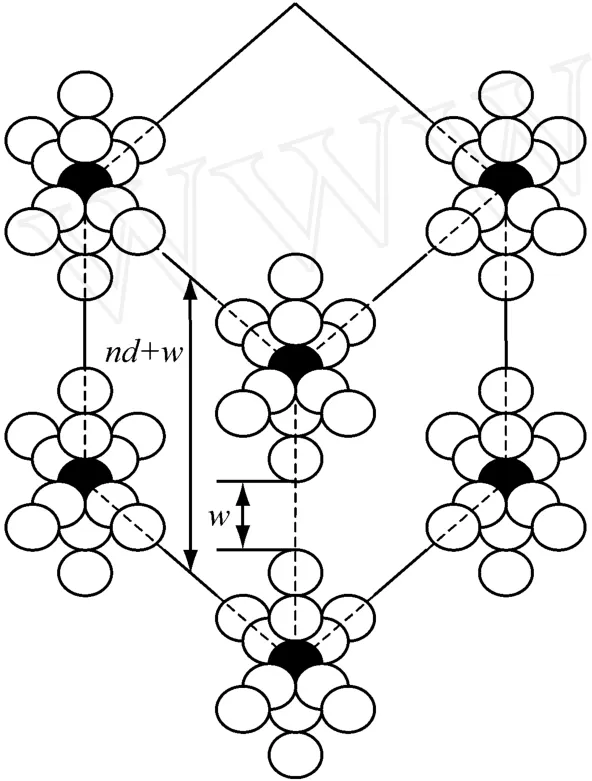
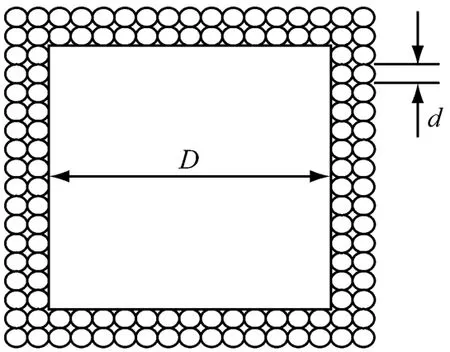
式中:σ,σ0为复合材料的电导率和高电导率组分的电导率;T1,T0为与温度有关的参数;A为导体横截面积;k为波耳兹曼常数;Φ为隧道势垒高度。当T< Simmons[22]提出了更具普适性的隧道效应方程: 式中:J为电流密度,m和e分别为一个电子的质量和电荷量,h为普朗克常数,φ为间隙势垒,D为间隙宽度,U为电势差。方程(6)中,电流密度J是隧道间隙宽度D的函数。 Ezquerra等人[23]推导出了导电复合材料电阻率与导电粒子间距的关系式: 式中:Xt=(2mW/h2)1/2,d是导电粒子间距,W为间隙势垒。若导电粒子在基体中是无规分布的,则导电粒子平均间距与1/V1/3成正比[24](V是复合材料中导电粒子的体积分数)。上式两边取对数可得logσ与1/V1/3之间成线性关系[23]。 Sherman[25]利用宏观的逾渗理论与隧道导电机理对导电复合物的逾渗行为及电阻率的正温度系数特性给予了解释。但是他无法解释当导电填料的体积分数大于逾渗阈值时,电导率不依赖于粒子间隙变化而变化的关系。 吴弛飞等人[19]通过理论与实验两方面的研究,在上述理论的基础上结合热膨胀观点提出了一种碳黑粒子分散状态的晶格模型,并得到能够较精确地计算复合材料电阻率的关系式,并证实了热起伏诱导隧穿机理的正确性。吴驰飞等人借助TEM及SAXS分析发现:在导电复合材料中由导电粒子相互接触的集团是不连续的,它们之间存在间隙。由此提出粒子分布晶格模型,如图1所示。图1中:d为碳粒子直径,nm;N为沿轴方向单位晶格的碳粒子平均数目。按照该模型,得到了碳黑粒子的体积分数V及其间距ω的表达式: 若忽略碳黑粒子间的接触电阻及其本身的电阻,则可得到整个材料的电阻网络,并推出如下关系式: 式中:T0=637AΦ3/2/ω2,A为导体的横截面积,Φ为隧穿势垒高度。 图1 碳黑粒子在基体中的分散状态晶格模型Fig.1 The crystal lattice model of the carbon black particles dispersed in matrix 根据吴弛飞等人的模型可得:室温下碳黑粒子间隙在1.2~1.7 nm范围内时亦有电流产生。这也与导电通道学说在1 nm以内才能出现导电现象的说法相背。根据此模型得到的结果与实验结果吻合得较好,可以认为该模型能近似地描述基体内导电粒子的分散状态。 Beek等人[26]认为高分子基导电复合材料的非线性导电行为是由隧道效应造成的,但这是导电粒子间强电场导致电子迁移的特殊情况。他们提出:虽然导电粒子之间存在绝缘的基体,但当导电粒子距离小于10 nm时,这些粒子之间所具有的强大电场可能使电子越过树脂界面势垒而跃迁到邻近的导电粒子上,从而产生电流,即:场致发射理论。其表达式为: 式中:J为电流密度,E为场强,A为隧道频率,n和 B为复合材料的特性常数,n一般介于1~3之间。场致发射理论由于受温度及导电填料的质量分数影响较小,因此,相对于逾渗理论和有效介质理论具有更广泛的适用范围。 金日光[27]等采用群子统计理论推导了有关复合导电高分子材料的电导率与组成关系的两参数性群子方程: 式中:σ为复合材料的电导率,σmin为低电导率组分的电导率,σmax为高电导率组分的电导率,x为导电填料的质量分数,r1,r2分别为表征导电粒子和基体群聚作用的参数。金日光等人根据上述理论,预测了5种电导率与组成关系的曲线,认为目前只存在 r1>1,r2>1以及r1>1,r2<1两种类型的曲线,其它3种曲线类型有待进一步实验发现。 影响复合材料导电性能因素的复杂性促使人们试图提出基于复合材料最终微观结构参量的导电模型[3,28]。Rajagopal[3]建立了一种简单几何模型,用来解释导电和绝缘粒子经干燥预混后直接烧结成型的复合材料的非线性导电行为。此模型假定绝缘粒子变形为基本规则的简单几何形状,并且导电粒子规则地分布在绝缘粒子表面。主要参数是成型后绝缘基元的边长D和导电粒子的直径d,如图2所示。此模型给出以下关系式: 式中:σ是混合物电导率,σf,Vf是导电粒子电导率和体积分数,r是相邻导电粒子接触面半径。 图2 复合材料导电基元的截面图Fig.2 The section picture of the conductive element in the composites 刘金世[1]等人建立了一种电导率模型。此模型考虑了导电颗粒形状对导电高分子复合材料的影响。他们利用该模型对碳纤维聚酯树脂复合材料的有效电导率进行了计算,计算结果与实验结果吻合较好。他们认为:在导电高分子复合材料中,由于分散的导电颗粒的量子隧道效应等原因,使得导电颗粒的有效导电体积增大。所以导电高分子复合材料就可看作由有效导电颗粒和绝缘高分子基体构成。由此得到的计算导电高分子复合材料有效电导率的公式为: 式中:φe为所有导电颗粒的有效体积分数,导电高分子复合材料的有效电导率为σe,有效导电颗粒的电导率为σc,高分子颗粒的电导率为σm,Bc,x为有效导电颗粒沿x方向的退极化因子,σc,x为有效导电颗粒沿x方向的电导率。 上述推导过程中没有考虑两相颗粒之间的相互影响。但随着导电颗粒的体积分数增加,必须考虑两相颗粒之间的近场影响。为此,他们引入一组来代替实际电导率σc(σm)。这样既考虑了介质自身的电导性质,又考虑了周围介质的影响。如果导电高分子复合材料中所有颗粒近似为球形,则可以得到计算导电高分子复合材料有效电导率的公式为: 刘金世等人的模型把有效电导率描述为各组成成分的体积分数、形状和颗粒尺寸的函数。利用该模型,得出了渗流阈值与导电颗粒的半径及轴长比的关系,以及导电高分子复合材料的有效电导率随导电颗粒轴长比和半径变化的规律。该导电高分子复合材料的有效电导率模型同样适用于导电高分子复合材料的其他渗流特性的计算,如热导率的计算等。 张雄伟等[29]认为低密度聚乙烯/碳黑复合材料的导电性是由于导电通道、隧道效应和场致发射三种机理综合作用的结果。 高分子基导电复合材料的导电机理非常复杂,除了上述一些较具代表性的理论之外,还有通用混合理论[30]、关键通路理论[31]等其它一些理论。 量子力学隧道效应理论能合理地解释高分子基导电复合体系中,导电粒子不直接接触也能导通的现象,并且此理论能与许多高分子基导电复合体系的实验数据相符。因此是分析高分子基导电复合材料非线性导电行为的有效工具。但隧道效应理论中,复合材料的电导率与导电粒子的间隙宽度及其分布状况有关;而导电填料的体积分数是影响导电粒子间距和分布的最重要因素。当导电填料的体积分数很小时,导电粒子间间隙过大,无法发生电子的隧穿,因此,隧道效应导电机理只能在某一导电填料的体积分数范围内才适用。实际上,复合材料的非线性导电行为通常是量子力学隧道效应和导电通道等若干导电机理协同作用的结果。当导电填料的体积分数较小时,导电粒子无法形成导电通道,此时只有量子力学隧道效应在起作用;当导电填料的体积分数较大时,复合材料的导电行为是导电通道和隧道效应共同作用的结果。因此,考察各导电机理之间的相互关系以及考虑影响复合材料导电行为的各种因素以提出更具有普适性的导电理论是今后研究的重要课题。 [1] 刘金世,薛庆忠.导电高分子复合材料的有效电导率模型[J].石油大学学报:自然科学版,2005,29(1):140-143. [2] 郑强,沈烈,李文春,等.导电粒子填充 HDPE复合材料的非线性导电特性与标度行为[J].科学通报,2004,49(22): 2 257-2 267. [3] Rajagopal C,Satyam M.Studies on electrical conductivity of insulator-conductor composites[J].J Appl Phys,1978, 49(11):5 536-5 542. [4] Kirkpatrick S.Nature of percolation’channels’[J].Solid State Communications,1973,12(12):1 279-1 283. [5] Miyasaka.K.Conductive mechanism of conductive polymer composites[J].InternationalPolymer Science and Technology,1986,13(6):41-45. [6] Sumita M,Takenaka K.Characterization of dispersion and percolation of filled polymer molding time and temperature dependence of percolation time on carbon black filled low density polyethylene[J]. Composite Interface,1995, 3(2):253-262. [7] Mclachlan D S.An equation for the conductivity of binary mixtures with anisotropic grain structures[J].J Phys C: Solid State Phys,1987,20(7):865-877. [8] Wessling B.Electrical conductivity in heterogeneous polymer systems,V(1):Further experimental evidence for a phase transition at the critical volume concentration[J]. Polym Eng Sci,1991,31(16):1 200. [9] Sumita M,Asai A,Niyadera N,et al.Electrical conduc-tivity of carbon black filled ethylenevinyl acetate copolymer as a function of vinyl acetate content[J].Colloid Polym Sci,1986,264(2):212-217. [10] Sumita M,Sakata K,Asai S,et al.Dispersion of filler and the electrical conductivity of polymer blends filled with carbon black[J].Polym Bull,1991,25(2):265-271. [11] Mclachlan D S.Equations for the conductivity of macroscopic mixtures[J].J Phys C:Solid State Phys,1986,19 (9):1 339-1 354. [12] Wessling B.Electrical conductivity in heterogeneous polymer systems,(IV):A new dynamic interfacial percolation model[J].Synth Met,1988,27(1):83. [13] Mclachlan D S.Measurement and analysis of a model dual-conductivity medium using a generalized effective medium theory[J].J Phys C:Solid State Phys,1988,21(8): 1 521-1 532. [14] Sichel E K,Gittleman J I,Sheeng P.Carbon black polymer composites:The physics of electrically conducting composites[J].Plastics Engineering,1982,3(1):53-59. [15] Sheng P,Sichel E K,Gittleman J I.Fluctuation-induced tunneling conducting in carbon-polyvinylchloride composites[J].Phys Rev Lett,1978,40(18):1 197-1 200. [16] Cashell E M,Coey J M D,Wardell G E,et al.DC electrical conduction in carbon black filled cis-polybutadiene [J].J Appl Phys,1981,52:1 542. [17] 舒启清.电子隧穿原理[M].北京:科学出版社,1998. [18] Polley M H,Boonstra B B S T.Carbon blacks for highly conductive rubber[J].Rubber Chemistry and Technology,1957,30:170-179. [19] 罗延龄,王庚超,张志平.PTC特性的复合导电体系中炭粒子分布的逾渗模型与电阻率的计算[J].高分子通报, 1998(4):23-33. [20] Voet A.Temperature effect of electrical resistivity of carbon black filled polymers[J].Rubber Chemistry and Technology,1981,54(1):42-50. [21] Shklovskii B I,Efros A L.Electronic properties of doped semiconductors[M].Berlin,1984,59:432-454. [22] Simmons J G.Generalized formula for the electric tunnel effect between similar electrodes separated by a thin insulating film[J].J Appl Phys,1963,34(6):1 793. [23] Ezquerra T A,Kulescza M.Charge transport in polyethylene-graphite composite materials[J].Adv Mater,1990, 2(12):597-600. [24] Boettger H,Bryksin U V.Hopping conduction in solids [M].Berlin:Berlin Verlag Akademie,1986:108-148. [25] Sherman R D,Middleman L M.Electron transport processes in conductor-filled polymers[J].Polym Eng Sci,1983,23:36. [26] Van Beek,Van Pul.Internal field emission in carbon black-loaded naturalrubbervulcanizates[J].J Appl Polym Sci,1962,24:651-655. [27] 金日光,连娜.复合型导电高分子材料电导率与组成关系的群子分析[J].北京化工大学学报:自然科学版,1996, 23(1):17-21. [28] Lux E.Models proposed to explain the electrical conductivity of mixtures made of conductive and insulating materials[J].J Mater Sci,1993,28(2):285-301. [29] 张雄伟,黄锐.LDPE/炭黑复合导电材料性能的研究[J].中国塑料,1994,8(3):26. [30] Uvarov N F.Estimation of composites conductivity using a general mixing rule[J].Solid State Ionics,2000,(136-137):1 267-1 272. [31] Sheng P,Klafter J.Hopping conductivity in granular disordered systems[J].Phys Rev B,1983,27(4):2 583.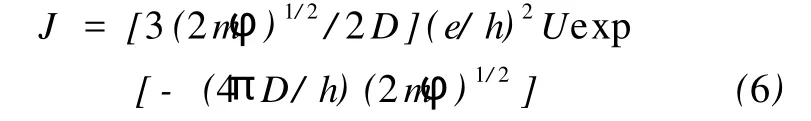

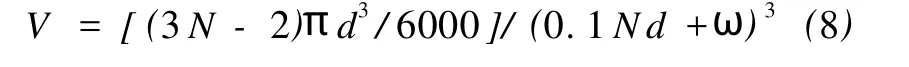
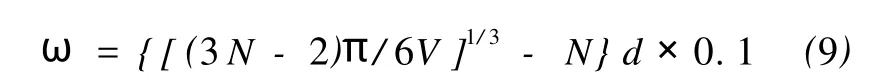

2 其它理论
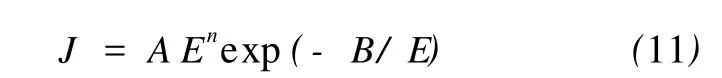


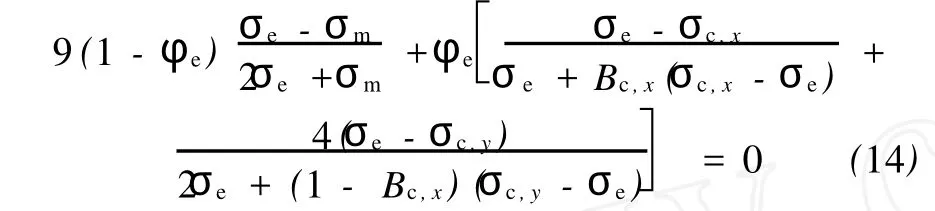
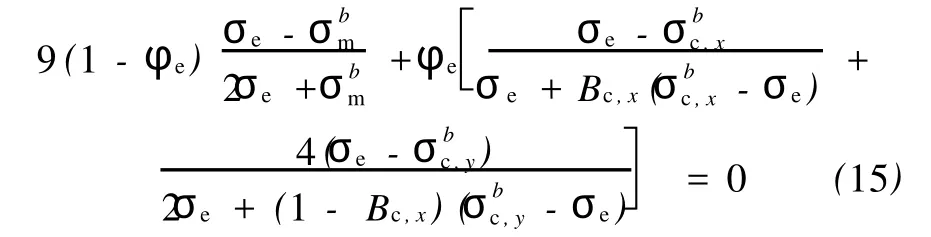
3 结论
