粗差分布及其随机数产生
2010-01-29李国重夏云青焦慧平
李国重,夏云青,焦慧平
(1.信息工程大学理学院,郑州 450001;2.中州大学信息工程学院,郑州 450044)
0.引言
在对加工工件的测量数据处理中,经常需要对新的测量平差理论或方法进行评估,其中一项重要工作是检验新理论或新方法抵御粗差的能力 (粗差是指离群的大误差[1,2],由失误等引起,它实际不可避免)。如果新理论或新方法能够有效地抵御粗差的不良影响,那么认为新理论或新方法有效,从而在测量数据处理中可以大胆使用;否则,我们怀疑新理论或新方法的效能,需谨慎使用或者弃之不用[3]。理论上讲,一个性能优良的平差理论能够抵御观测数据的任何粗差,无论这些粗差分布在哪些观测数据中以及粗差的量级多大。然而,检验平差理论抵御粗差的能力并非易事,尤其在观测数据量很大时 (不妨设有 1000个观测数据)。如果这些观测数据中仅有一个粗差,粗差在观测数据中的位置有1000种可能性 (每个观测数据都可能包含此粗差)。为此我们需要进行 1000次检验,若成功探测出粗差 1000次,则新理论探测粗差的效能达到 100%;若成功 900次,则探测粗差的效能就是 90%。如果测量数据中含有 2个粗差,这两个粗差在观测数据中的位置就有 C21000=499500种可能性,为此要进行 499500次检验,如果有 3个粗差呢?要进行=166167000次检验,要进行如此多次数的检验,很明显这是不现实的[4]。如何设计检验方案,达到既能科学评估新的平差理论和方法效能的目的,又能使检验次数有限,在实际工作中非常必要。这就需要探讨粗差的分布,依据其分布设计检验方案。
值得注意的是,以往讨论粗差分布的文章很少[5],且粗差在观测数据中的位置和大小具有随意性,基于随意性基础上的平差理论评估是不可靠的[6]。
1.粗差个数的分布
大量观测数据的统计分析表明,粗差在观测数据中占少数,一般情况,含粗差的观测数据占数据总量的 1%~10%[2,4],大部分观测数据是正常的。
假定有 n个观测数据,且观测数据相互独立。每个观测数据含有粗差的概率相等,都等于 p(p一般为 1%~10%)。设这 n个观测数据中含有 X个粗差,显然 X是随机变量,可能取到 0,1,2,…,n这些值。由概率论知识知:粗差个数 X服从二项分布,即 X~b(n,p)。
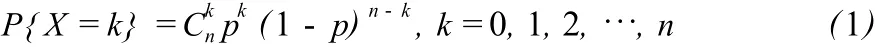
在测量数据处理中可以取 X的平均值 (数学期望)E(X)=np作为粗差个数的估值。因粗差个数是整数,所以一般要对平均值舍入取整数,假定取整后粗差个数是 m=[np]。
2.粗差位置和大小的联合分布
用上述方法确定了 n个观测数据中含有 m个粗差,那么这 m个粗差到底分布在哪些观测数据上呢?粗差的大小又该如何确定呢?下面将详细分析这些问题。
2.1 单个粗差位置和大小的联合分布
首先讨论单个粗差Δ位置 Y和大小 Z的联合分布。单个粗差Δ以等可能分布在每个观测数据上,所以粗差的位置 Y分布是离散均匀分布,即
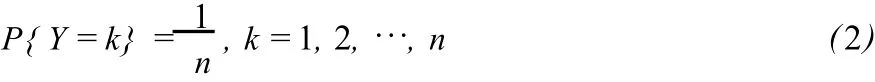
单个粗差Δ的大小分布可以按如下方法确定。由于测量误差通常服从正态分布,一般认为 3σ(σ是标准差)之外的误差为粗差。基于上述认识,可以构造一个粗差分布,粗差Δ在 (-3σ,+3σ)内概率密度为 0,在 3σ之外服从正态分布,即粗差Δ大小的概率密度函数为:
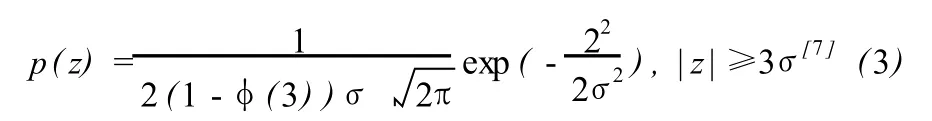
由于此分布是在正态分布基础上提出的,而且只在两端有密度,故本文称之为截尾正态分布。
综上所述,可得粗差Δ所在位置 Y和大小 Z的联合分布函数 (称为离散均匀 -截尾正态分布)为:
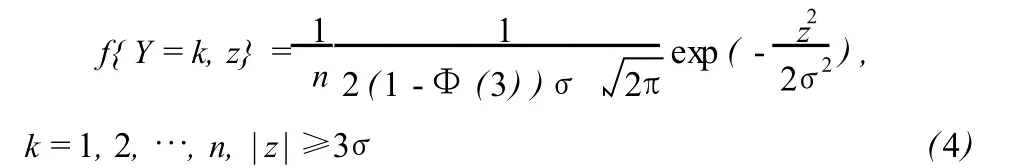
很明显,粗差Δ所在的位置和大小 (Y,Z)的联合分布既不是离散型随机变量,也不是连续型随机变量,它属于非离散非连续型随机变量。
如果 n个观测数据的权重不同,则观测误差不同,因此粗差的界定不同。不妨设第 k个观测数据的权重为 pk,此时(3)式可改写为:
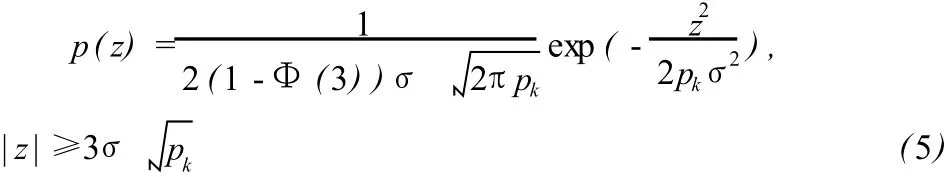
根据 (2)式和 (5)式,可以推出粗差Δ所在的位置和大小 (Y,Z)的联合概率分布为:
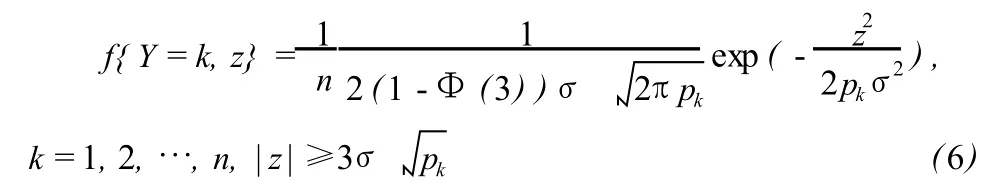
2.2 多个粗差位置和大小的联合分布
因为每个观测数据含有粗差的概率相同,自然认为这 m个粗差Δ(粗差向量)离散均匀分布在 n个观测数据上。这相当于 m个学生离散均匀分布在 n个不同的座位上,共有可能性,即
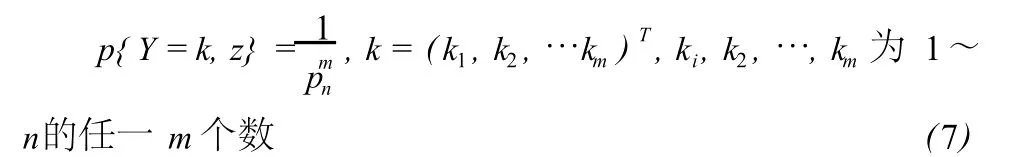
由此,知粗差向量所在的位置和大小 (Y,Z)也服从离散均匀——截尾正态分布,其联合分布为:
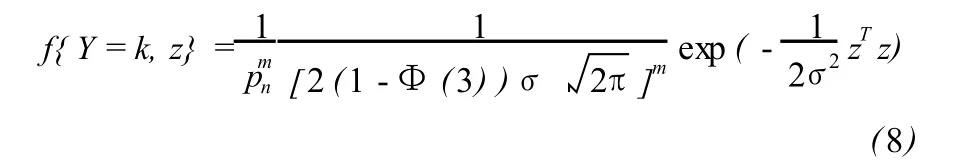
如果 n个观测数据的权重不同,不妨设第 k个观测数据的权重为 pk,经过和(6)式类似地推导可得粗差向量Δ所在的位置和大小 (Y,Z)的联合概率分布为:
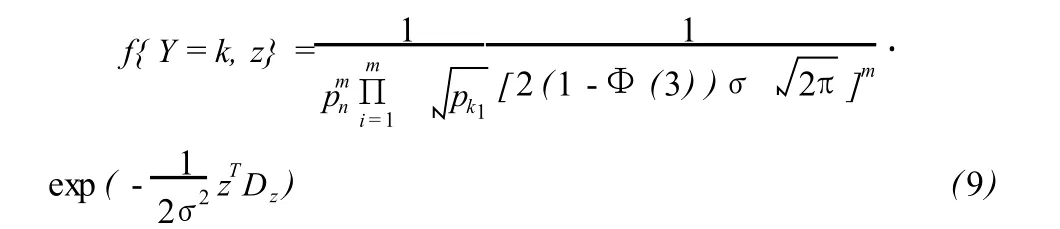
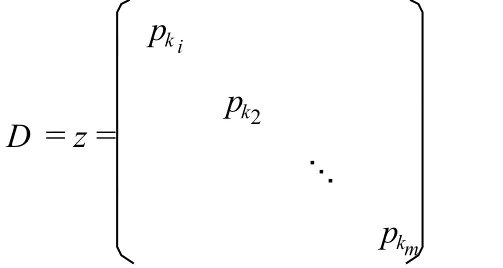
3.粗差分布的随机产生方法
假定观测数据相互独立而且等权,下面将讨论利用Matlab[8]软件产生粗差随机数的方法。
第一步,用函数 round()对粗差个数的数学期望舍入取整,得到粗差个数 。
第二步,用 unidrnd()产生离散均匀分布函数的随机数。
第三步,可通过编程来产生截尾正态分布的随机数。首先产生正态随机数,保存正态随机数的正负号,然后对正态随机数取绝对值,再向右平移 3σ,最后再把保存的正负号再添加到相应的经过平移后的随机数上。
具体的程序如下:
clc;clear
disp(’设定观测数据n=40,粗差概率p=0.1,取整后粗差数 m=4,标准差 sigma=1,重复试验次数 k=10′)
n=40;p=0.10;m=round(n*p);sigma=1;k=10;
disp(’产生k组符合要求的m个离散均匀分布′)
l=unidrnd(n,k,m);
for i=1:k
I=0;
for j=1:m-1
for jj=j+1:m
if l(i,j)= =l(i,jj)
I=I+1;
end
end
end
while I>0
l(i,:)=unidrnd(n,1,m);I=0;
for j=1:m-1
for jj=j+1:m
if l(i,j)= =l(i,jj)
I=I+1;
end
end
end
end
end
l
disp(’产生k组符合要求的m个截尾正态随机数(每组一行,每一行 m个粗差)
t=nor mrnd(0,1,k,m);
%disp(’保留每个随机数的正负号’)
fuhao=sign(t);
%disp(’每个随机数取绝对值’)
tt=abs(t)+3*sigma;
%disp(’截尾正态分布随机数’)
for j=1:m
for i=1:k
x(i,j)=fuhao(i,j)*tt(i,j);
end
end
x
整理程序运行结果后,得到:
设定观测数据 n=40,粗差概率 p=0.1,取整后粗差数m=4,标准差 sigma=1.0,重复试验次数 k=10
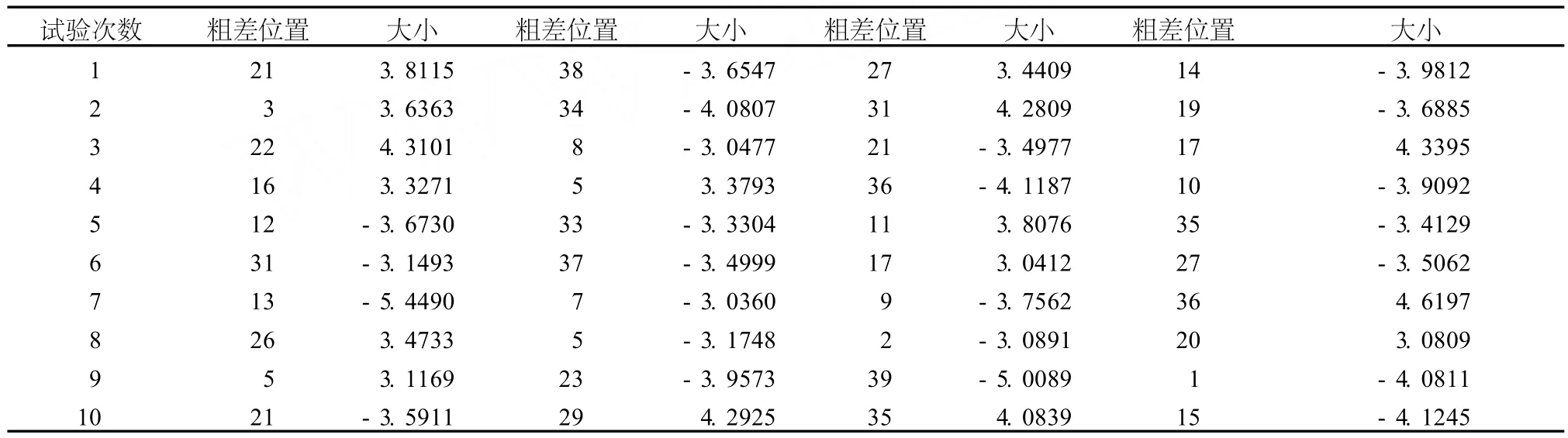
表1
4.结论
(1)粗差个数服从二项分布,粗差的位置和大小的联合分布为离散均匀——截尾正态分布,并可用Matlab软件产生了联合分布的随机数。这是科学评价新的平差理论和方法的基础条件和先决条件。
(2)在产生离散均匀——截尾正态分布随机数的过程中有可能在一个观测数据上出现两个或多个粗差的情况,这在测量数据处理中是不允许出现的,此时在程序中应舍弃本次试验,重新产生符合要求的随机数的方法来处理。
[1]周江文.经典误差理论与抗差估计[J].测绘学报,1989,18(2):115-120.
[2]周江文,欧吉坤,杨元喜.测量误差理论新探 [M].北京:地震出版社,1999:6-8.
[3]哈尔滨工业大学,上海工业大学.机床夹具设计 [M].上海:上海科学技术出版社,1985.
[4]刘友才,肖继德.机床夹具设计[M].北京:机械工业出版社,1992.
[5]华中工学院标准化与计量测试教研室.互换性与技术测量[M].武汉:华中工学院出版社,1983.
[6]刘登平.机械制造工艺及机床夹具设计 [M].北京:北京理工大学出版社,2008.
[7]Peiliang Xu.Sign-constrained robust least squares,subjective breakdown point and the effectofweightsof observations on robustness[J].J.of Geod.2005(79):146-159.
[8]Huber P J.Robust Statistics[M].New York:John W iley&Sons,1981.
