源于惠更斯碰撞理论的高考试题探析

2010-01-26刘立雪

物理通报 2010年8期

关键词：命制小球异化

刘立雪

(天津市宝坻区第一中学天津 301800)

1 惠更斯碰撞理论

惠更斯从1652年开始研究弹性物体之间的碰撞，1656年把自己的结果收集在论文《论碰撞作用下物体的运动》中.下面对惠更斯碰撞理论作出简要介绍.

1.1 三个假设(公理)

(1)任何运动物体只要不遇障碍，将沿直线以同一速度运动下去.

(2)两个相同的物体做对心碰撞时，如碰前各自具有相等相反的速度，则将以同样的速度反向弹回.

(3)物体的运动以及它们的速度，必须看作是相对于另一些我们以为是静止的物体而言的，而不必考虑这些物体是否还参与另外的共同运动.因此，当两个物体相碰撞时，即使它们同时参与另一匀速运动，在也具有这个共同运动的观察者看来，两个物体的相互作用就好像不存在这个共同运动一样.

1.2 三个实验

(1)如图1所示，两个质量相同并以相同的速度相向运动的物体，在发生刚性的对心碰撞之后，都保留碰撞前的速度而相互弹开.

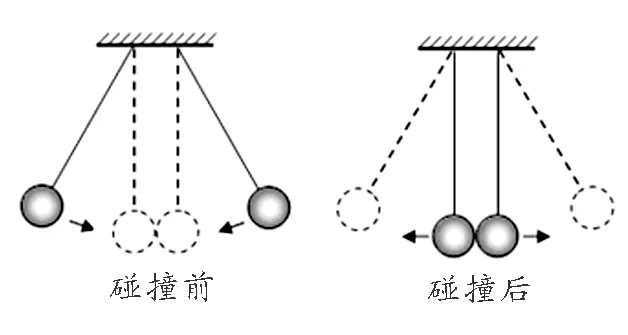
图1 惠更斯碰撞实验之一

(2)如图2所示，一个静止的球同一个质量相同的运动着的球碰撞后，后者立即停止，而原来静止的球则获得这一个速度前进.

图2 惠更斯碰撞实验之二

(3)惠更斯独具匠心地设计了一个巧妙的理想实验，如图3所示.设船以速度u向右行驶.若船上的人在他的参考系内做图1所示的实验，则在岸上的人看来，碰前两球以速度v+u和v-u相向运动；碰撞后两球以速度v-u和v+u反弹.于是，惠更斯便得到了相同的球以不同的速度做对心弹性碰撞，彼此将会交换速度的普遍结论.

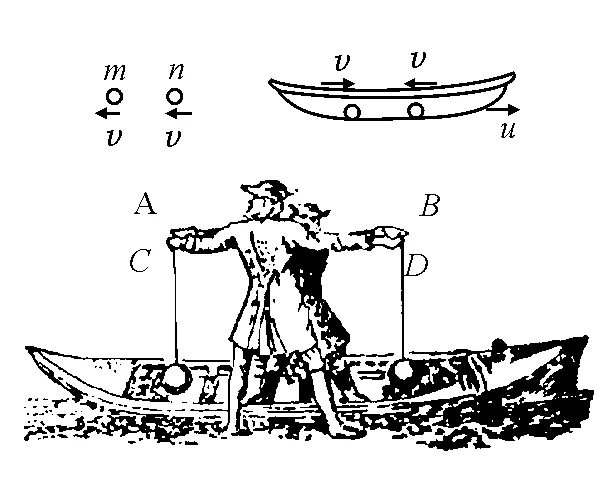
图3 惠更斯的想象：两相等质量间的弹性碰撞

1.3 两条结论

(1)两个物体所具有的运动量在碰撞中都可以增多或减少，但是它们的量值在同一个方向的总和却保持不变，如果减去反方向的运动量的话.

(2)两个、三个或任意多个物体的共同重心，在碰撞前后总是朝着同一方向做匀速直线运动.

2 高考试题探析

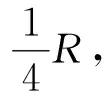
(1)待定系数β;

(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力;

(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度，并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度.

解：(1)由

得

β=3

(2)设 A、B 碰撞后的速度分别为v1、v2，则

设向右为正、向左为负，依据动量守恒定律

解得

方向向左.

方向向右.

设轨道对 B 球的支持力为N， B 球对轨道的压力为N′，方向竖直向上为正、向下为负．则

N′=-N=-4.5mg

方向竖直向下.

(3)设 A、B 球第二次碰撞刚结束时的速度分别为v1′、v2′，则

-mv1-βmv2=mv1′+βmv2′

解得

v2′=0

(另一组解：v1′=-v1，v2′=-v2不合题意，舍去)

由此可得:

当n为奇数时，小球 A、B 在第n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同；

当n为偶数时，小球 A、B 在第n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同.

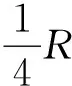
【例2】(2007年高考全国理综卷Ⅰ第24题)如图4所示，质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂.现将绝缘球拉至与竖直方向成θ=60°的位置自由释放，下摆后在最低点与金属球发生弹性碰撞.在平衡位置附近存在垂直于纸面的磁场.已知由于磁场的阻尼作用，金属球将于再次碰撞前停在最低点处.求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°.

图4

解：设在第n次碰撞前绝缘球的速度为vn-1，碰撞后绝缘球、金属球的速度分别为vn和vn′，由于碰撞过程中动量守恒，碰撞前后动能相等.设速度向左为正，则

mvn-1=Mvn′-mvn

(1)

(2)

由(1)，(2)两式及M=19m解得

(3)

(4)

第n次碰撞后绝缘球的动能为

(5)

E0为第1次碰撞前的动能，即初始能量.

绝缘球在θ0=60°与θ=45° 处的势能之比为

(6)

式中l为摆长.

根据(5)式，经n次碰撞后

易算出(0.81)2=0.656,(0.81)3=0.531，因此，经过三次碰撞后θ将小于45° .

点评：本题以惠更斯碰撞实验之二为题源，具体命制试题时主要进行了三处异化处理.

(1)将等摆长异化为不等摆长；

(2)将两等质量间的弹性碰撞异化为两不相等质量间的弹性碰撞；

(3)将重力场异化为复合场.试题命制的亮点是条件“已知由于磁场的阻尼作用，金属球将于再次碰撞前停在最低点处”的巧妙设置——每次碰撞都出现在最低点，进而使试题蕴含递推关系.

试题考查的重点是弹性碰撞过程中的两个守恒定律，考查的难点是应用数学知识处理物理问题，特别是递推关系的处理.

【例3】(2005年高考江苏物理卷第18题)三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上.现给中间的小球B一个水平初速度v0，方向与绳垂直，小球相互碰撞时无机械能损失，轻绳不可伸长.求：

(1)当小球A、C第一次相碰时，小球B的速度；

(2)当三个小球再次处在同一直线上时，小球B的速度;

(3)运动过程中小球A的最大动能EkA和此时两根绳的夹角θ;

(4)当三个小球处在同一直线上时，绳中的拉力F的大小.

解：(1)设小球A、C第一次相碰时，小球B的速度为vB.考虑到对称性及绳的不可伸长特性，小球A、C沿小球B初速度方向的速度也为vB，由动量守恒定律，得

mv0=3mvB

由此解得

(2)当三个小球再次处在同一直线上时，则由动量守恒定律和机械能守恒定律，得

mv0=mvB+2mvA

解得

三球再次处于同一直线.

另一组解

vB=v0vA=0

为初始状态，舍去.

所以三个小球再次处在同一直线上时，小球B的速度为

负号表明与初速度方向相反.

(3)当小球A的动能最大时，小球B的速度为零，设此时小球A、C的速度大小为u，两根绳间夹角为θ，则仍由动量守恒定律和机械能守恒定律，得

另外

由此可解得，小球A的最大动能为

此时两根绳间夹角为θ=90°.

(4)小球A、C均以半径L绕小球B做圆周运动.当三个小球处在同一直线上时，以小球B为参考系(小球B的加速度为零，为惯性参考系)，小球A、C相对于小球B的速度均为

v=|vA-vB|=v0

所以，此时绳中拉力大小为

点评：本题以惠更斯碰撞实验之一为题源，具体命制试题时主要进行了两处异化处理.

(1)将碰撞平面由竖直平面异化为光滑水平面；

(2)将摆的悬点异化为第三球.试题的命制亮点是本题的物理情景与图3所述情况有异曲同工之妙.本题“悬点”的速度方向与两球碰撞时速度方向垂直，而图3中悬点的速度方向与两球碰撞时的速度方向平行，试题的深刻思想是惠更斯碰撞理论中假设(3),即运动的相对性.

试题考查的重点是弹性碰撞过程中的两个守恒定律，难点是周期性物理情景的建立.

【例4】(2007年高考重庆卷理综卷第25题)某兴趣小组设计了一种实验装置，用来研究碰撞问题，其模型如图5所示.完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔，从左到右，球的编号依次为1,2,3,…N，球的质量依次递减，每球质量与其相邻左球质量之比为k(k<1) .将1号球向左拉起，然后由静止释放，使其与2号球碰撞，2号球再与3号球碰撞……所有碰撞皆为无机械能损失的正碰.(不计空气阻力，忽略绳的伸长，g取10 m/s2)

图5

(1)设与n+1号球碰撞前，n号球的速度为vn,求n+1号球碰撞后的速度;

(2)若N=5,在1号球向左拉高h的情况下，要使5号球碰撞后升高16h(16h小于绳长),问k值为多少？

(3)在第(2)问的条件下，悬挂哪个球的绳最容易断，为什么？

解：(1)设n号球质量为mn,n+1号球质量为mn+1,碰撞后的速度分别为vn′、vn+1′, 取水平向右为正方向，据题意n号球与n+1号球碰撞前的速度分别为vn、0，又mn+1=kmn.

根据动量守恒，有

mnvn=mnvn′+kmnvn+1′

(7)

根据机械能守恒，有

(8)

由(7)、(8)得

其中vn+1′=0舍去.

设n+1号球与n+2号球碰前的速度为vn+1

据题意有

vn+1=vn+1′

得

(9)

(2)设1号球摆至最低点时的速度为v1,由机械能守恒定律有

(10)

(11)

同理可求，5号球碰后瞬间的速度

(12)

由(9)式得

(13)

N=n+1=5时

(14)

由(11)、(12)、(14)三式得

(15)

(3)设绳长为l,每个球在最低点时，细绳对球的拉力为F,由牛顿第二定律有

(16)

则

(17)

(17)式中Ekn为n号球在最低点的动能.

由题意1号球的重力最大，又由机械能守恒可知1号球在最低点碰前的动能也最大，根据(11)式可判断在1号球碰前瞬间悬挂1号球细绳的张力最大，故悬挂1号球的绳最容易断.

点评：本题以惠更斯碰撞实验之二为题源，具体命制试题时主要进行了三处异化处理.

(1)将两个球异化为N个球；

(2)将等质量间的弹性碰撞异化为不相等质量间的弹性碰撞；

(3)将球均在最低点静止时无间隔异化为球均在最低点静止时有微小间隔.试题命制的亮点是通过设置条件“球的质量依次递减，每球质量与其相邻左球质量之比为k(k<1) ”，使试题蕴含递推关系，增强了试题的探究性.

试题考查的重点是弹性碰撞过程中的两个守恒定律，考查的难点是应用数学知识处理物理问题，特别是递推关系的运算.

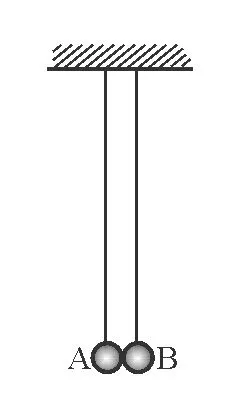
图6

【例5】(2008年高考宁夏卷理综卷第33-2)某同学利用如图6所示的装置验证动量守恒定律.图中两摆摆长相同，悬挂于同一高度，A、B两摆球均很小，质量之比为1∶2.当两摆均处于自由静止状态时，其侧面刚好接触.向右上方拉动B球使其摆线伸直并与竖直方向成45°角，然后将其由静止释放.结果观察到两摆球粘在一起摆动，且最大摆角成30°.若本实验允许的最大误差为±4%，此实验是否成功地验证了动量守恒定律？

解：设摆球A、B的质量分别为mA、mB，摆长为l，B球的初始高度为h1，碰撞前B球的速度为vB.在不考虑摆线质量的情况下，根据题意及机械能守恒定律有

h1=l(1-cos45°)

(18)

(19)

设碰撞前后两摆球的总动量的大小分别为p1、p2.有

p1=mBvB

(20)

联立(18)、(19)、(20)式得

(21)

同理可得

(22)

联立(21)、(22)式得