Paul阱中存储离子的研究

刘名扬,孙维谨

(装甲兵工程学院基础部,北京100072)

1 引 言

自发现原子以来,人们一直渴望观测到单个离子的行为,探索物质的基本结构和运动规律.为了探索研究原子、分子和离子等微观粒子的内部结构和运动规律,操作和控制单个微观粒子,就需要一个与外界隔绝的环境,使微观粒子的运动不受外界环境的影响.离子存储就是用电场和磁场把运动速度非常低的离子束缚在小区域内,持续相当长的时间,使用的装置称为离子阱.随着用于离子存储的离子阱[1]和激光冷却技术的不断发展,使实现这种隔离环境成为可能.在众多的离子阱中,Paul离子阱由于其优良的特性和先进的功能,在科学和技术等很多领域中得到广泛应用.利用Paul阱在对谱线的精确测量[2-3]、研究辐射场与带电粒子的相互作用、测量离子能态的寿命、详细观察离子间的碰撞过程以及研究离子的生成机制等方面取得了重大的成就.

2 Paul阱内离子的运动

Paul阱是利用四极电势构成三维势阱,把离子存储在阱内特定区域的装置,其电极结构的剖面图如图1所示.

Paul阱的内表面是由2个绕 z轴旋转的双曲面电极(称为帽电极,也称端电极)和1个以 xy平面为对称切面的双曲环形电极(称为环电极)组成.阱中的存储电势由加在环电极与帽电极之间的电压U+V cos(ωt)产生,其中:U为直流电压,犞为射频电压峰值,ω为射频场频率.这样,在Paul阱中就产生了周期性含时四极电势

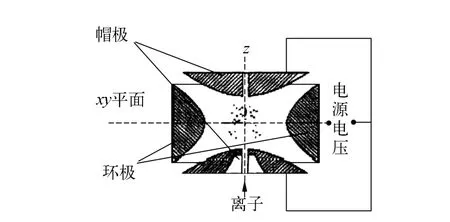
图1 Paul阱的电极结构剖面图

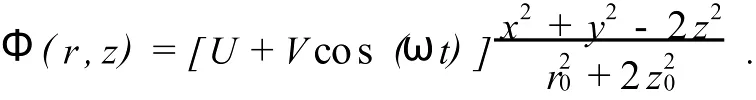
其中:2 r0为环电极的最小直径,2z0为上下端电极之间的最小间隔,二者之间满足 r20=2z20.这一电势分布使得阱中心形成一个电势极小,离子在阱中受到一个指向阱心的存储力的作用.

电量为Q,质量为m的离子在阱中受到的作用力为 F=-▽Φ(x,y,z).则离子在存储势场中的运动方程为[4]

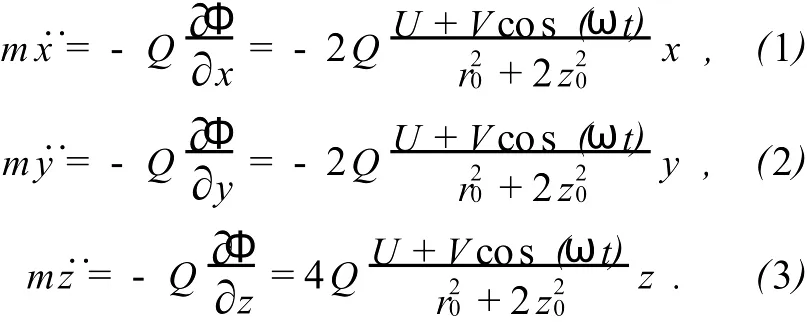
引入无量纲参数:

由式(1)～(3)可得到标准M athieu方程[5-7]

(4)式是3个非耦合的Mathieu方程,式中v1,v2,v3分别代表x,y,z.根据 Floquet定理,方程(4)具有如下形式的解

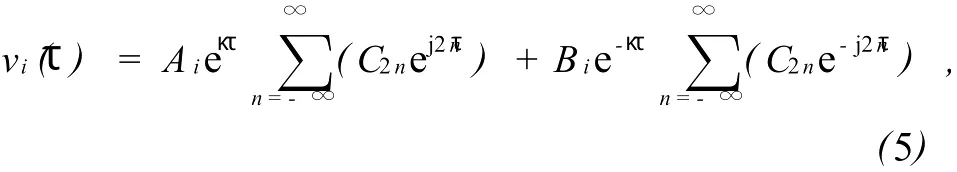
其中:C2n为满足一定递推关系的系数,κ=α+jβ,κ由参数a和q决定.从数学中关于微分方程的讨论知道这样的运动有稳定区和不稳定区.κ的取值将决定Mathieu方程的解是否稳定,只有 a和q处于稳定区时,离子才可能存储于阱中.由数学知识可知κ取值与稳定性有如下关系:a.当κ的值是不为0的实数时,vi随时间的增大而增大,解是不稳定的;b.当κ的值是实部不为0的复数时,解是不稳定的;c.当κ=i Z,Z=整数时,vi具有周期性,但不稳定;d.当κ=i Z,Z是不为整数的实数时,vi具有周期性且是稳定的.

为了能长时间地研究存储于Paul阱中的离子,就必须使离子做稳定运动,即M athieu方程的解(5)式必须取如下形式:

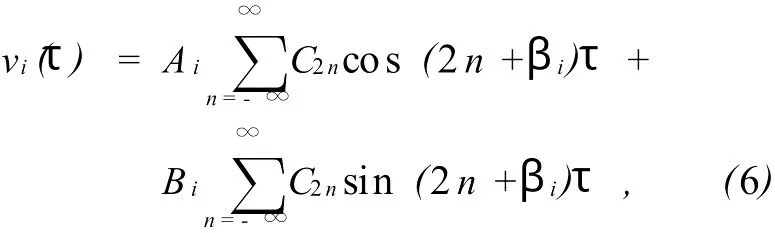
其中β是不为整数的实数.

用原来的量纲单位表示(6)式,则有

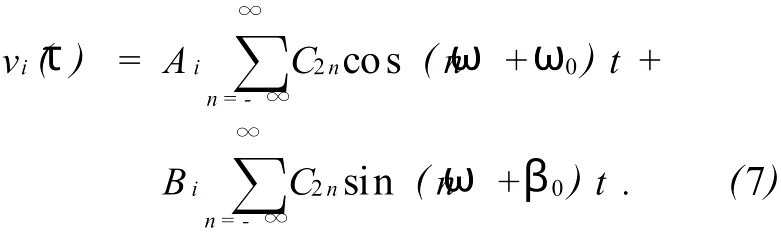
上述运动中的宏运动(即久期运动)反映离子在阱中运动的主要特征,如果离子微运动很小,可忽略微运动,这样离子的运动就简化为谐振子运动,Ψ为赝势.

3 实验与分析

硅原子团簇离子Si+n的碰撞实验是在如图2所示的射频离子阱进行的,射频离子阱由环电极、端电极、真空室、相关的控制系统、信号检测和数据采集系统组成.由于产生原子团簇和碰撞反应的需要,在通常的离子阱装置上增加了激光溅射系统.实验以硅粉为样品,倍频后的激光经会聚后,穿过端电极的一对小孔到达阱外的硅靶上.当靶表面的光斑直径小于1 mm时,激光功率密度可达107W/cm2,从而溅射出各种质量的硅团簇离子Si+n,激光脉冲后,快速建立适当的射频和直流电压,使得团簇离子到达阱中心时能将其捕获.为了囚禁某一质量的Si+n,需要对射频和直流电压进行精确的时序控制,以排除不需要的团簇离子和杂质离子.另外,在两端电极之间加一弱驱动电磁场进行检测,通过连续改变直流偏置电压U(这里利用了一锯齿波进行扫描)来改变离子的宏运动频率ωz,当离子的振动频率刚好等于弱驱动频率时,离子从驱动场中强烈吸收能量,通过示波器可以看到端电极两端的电压造成的下陷.这样利用一锯齿波扫描可以给出被囚禁在阱中不同质量的离子谱.

图2 射频离子阱装置示意图

在本实验中,实验条件如下:z0=7 mm,r0=9.9 mm,U=9.6 V,V=160 V,射频电压频率ω=2π×560 k Hz,检测频率ωz=2π×54 k Hz,囚禁参数 az=0.058,qz=0.44,βz=0.23,轴向阱深Dz=4.2 V,真空气压 p=10-7Pa.

当硅原子团簇离子Si+n经过选择存储后,继续囚禁若干时间,Si+n会由于碰撞而解离出一些小的碎片:Si+n-1,Si+n-2,….根据选择存储的团簇离子碰撞解离结果,可得到硅原子团簇离子Si+n(n=2～21)的电荷转移过程:

表1和表2给出Si+n(n=2～21)经碰撞诱发解离较小硅团簇离子Si+m(n＞m)的产额.由表1和表2给出的产额可知,尺寸在 n=7～21硅团簇离子经碰撞解离出团簇离子碎片时,Si+6,Si+10,Si+14,Si+18成分异常大,这表明 Si+6,Si+10,Si+14,Si+18是特别稳定的.图3给出了Si+16经碰撞裂解成较小团簇离子质谱.

表1 Si+n(n=2～11)分裂成较小团簇离子的产额

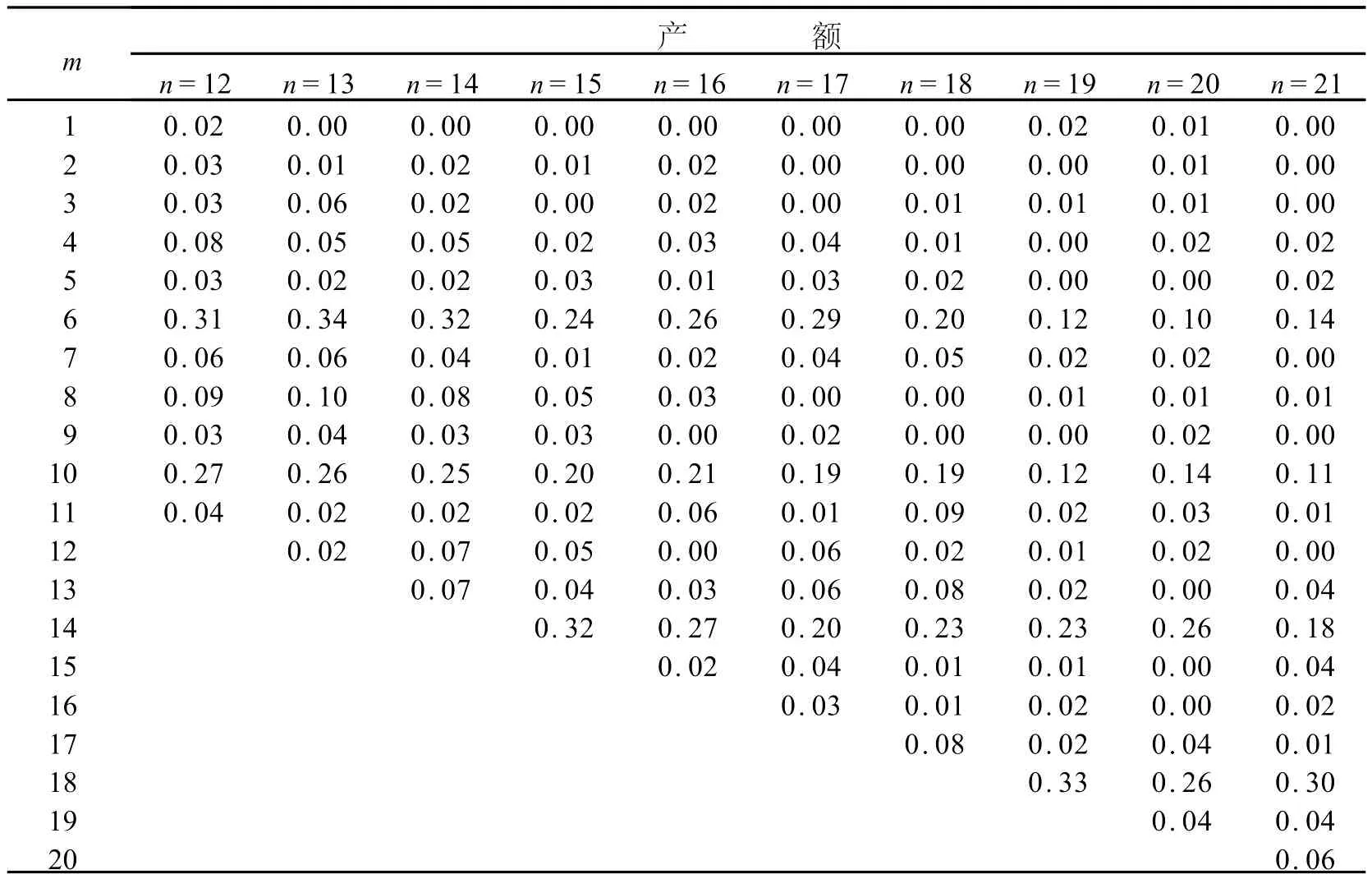
表2 Si+n(n=12～21)分裂成较小团簇离子的产额

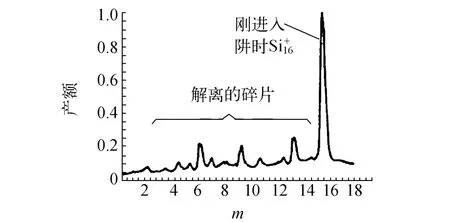
图3 Si+16经碰撞裂解成较小团簇离子质谱

Saito等人[8]较为详细地研究了sp3杂化原子间共价键相互作用的四面体性质,假定每个原子有一定的结构,围绕每个原子有4个“吸引中心”,构成规则的四面体形.取总能量最小来寻找T=0时的稳定结构,采用准牛顿法进行数值解,计算 n=2～18团簇的结构,如图4所示.当 n＞6时,取六原子环呈金刚石晶格结构(晶相序列)[8].Saito等人对 n=2～18团簇的结构进行分析,得出了 n=2～18团簇的配对分布函数(PDF),通过分析配对分布函数(PDF),得出 n=6,10,14,18时,硅团簇离子结构最为稳定.这与笔者通过碰撞诱发解离Si+n,分析其解离出较小团簇离子产额,得到 Si+6,Si+10,Si+14,Si+18是稳定的团簇离子的结论是一致的,这样就从实验上证明Saito理论的正确性.

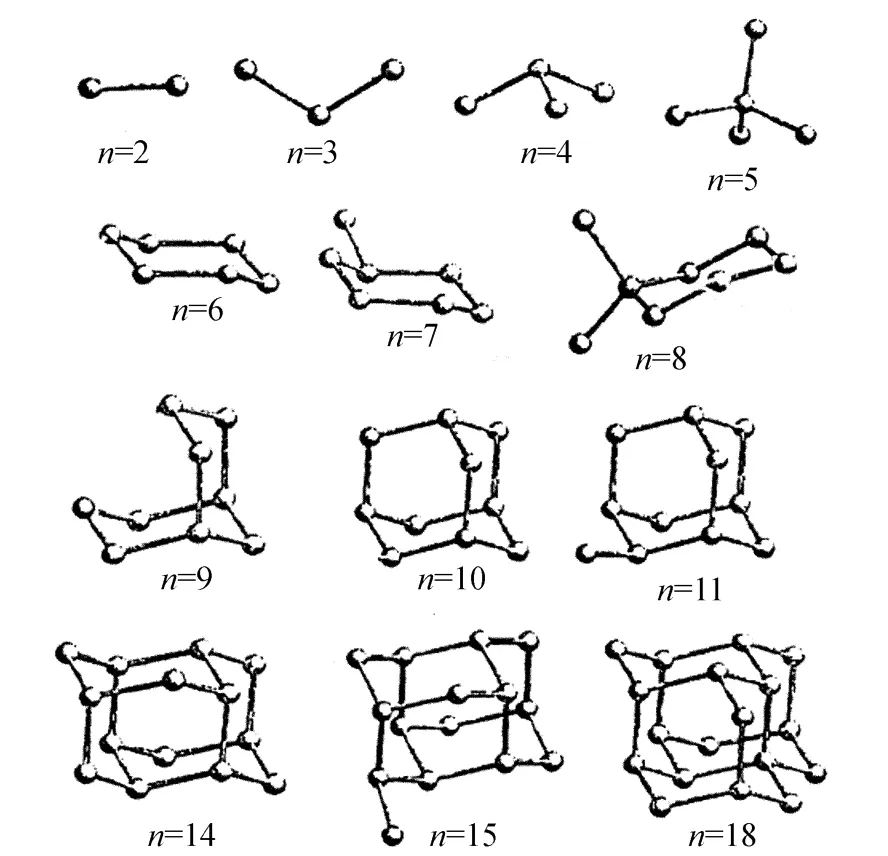
图4 利用四面体模型势计算得到的共价键团簇结构

4 结 论

在Paul阱第一稳定区的离子经激光冷却后,当初始条件合适时,离子的初速度不很大,离子的运动振幅小于器壁之间的距离,加之存储空间内气体非常稀薄,很少发生碰撞现象,离子可在存储空间内保持相当长的时间,室温下单个电子可以存储几个星期,离子可以存储几天.硅团簇离子为金刚石晶格结构,n=6,10,14,18时,硅团簇离子结构最为稳定.

[1] Hasegawa T,Bollinger J J.Rotating radio frequency in traps[J].Phys.Rev.A,2005,72:043403.

[2] Meekhof D M,Monroe C,King B E,et al.Simp le experimental methods for trapped-ion quanta p rocessors[J].Phys.Rev.Lett.,1996,76:1796.

[3] Kreuter A,Becher C.Experimental and theoretical study of the 3D-level lifetimesof 40 Ca+[J].Phys.Rev.A,2005,71:032504.

[4] 李燕,梁汉东,韦妙,等.离子阱质谱计的研究现状及其进展[J].质谱学报,2006,27(4):251.

[5] Moo re M,Blumel R.Quantum manifestation of o rder and chaos in the Paul trap[J].Phys.Rev.A,1993,48:3 082.

[6] Blumel R,Kapp ler C.Chaos and order of lasercooled ions in a Paul trap[J].Phys.Rev.A,1989,40:808.

[7] Hai W,Duan Y W.Stable orbits embedded in a chaotic attracto r for a trapped ion interacting w ith a laser field[J].J.Phys.A,1988,31:2 991.

[8] Saito S,Ohnishi S,Sugano S.Structures and magic numbersof group-IV microclusters calculated by use of an anisotropic model potential[J].Phys.Rev.B,1986,33:7 036-7 042.