基于模拟乘法器的超声多普勒黏度测量实验系统

李光仲,刘俊英

(滨州医学院a.物理教研室;b.内科教研室,山东滨州256603)

1 引 言

黏度η是表征液体黏滞性强弱的重要参量.测量液体黏度是大学物理实验的重要内容,目前实验室常用落球法进行测量[1].实验中由于液体的折射以及视觉暂留效应的影响,很容易产生视觉误差;同时,若小球偏离容器轴线非铅直下落,则小球终极速度的测量值与实际值间也存在较大的不确定度,使得测量精度无法保证.最后,实验过程中每次抛球只能测得1组数据,测量效率较低,易受外界干扰,可重复性差.

根据多普勒效应原理,利用实验室现有的数字存储示波器等设备,设计了超声多普勒黏度测量实验系统.该实验系统以落球法为基础,通过超声波发射器连续不断地向在液体中下落的小球发射超声波,利用接收器接收小球反射回来的超声波,然后由频移信号处理电路和数字存储示波器测量多普勒频移,应用多普勒效应原理准确地计算出小球的终极速度,进而得出液体的黏度.实验中超声波对小球定位准确,每次抛球可以连续测得3组数据,测量效率较高,可重复性较强.而且,本实验系统还可以开展超声测速、超声测距等与多普勒效应相关的设计性实验,以满足深入培养学生观察分析能力和动手能力的需要,同时也实现了实验资源的共享,提高了仪器设备的利用率.

2 实验原理

当半径为 r的金属小球,以速度 v在均匀的、各方向上无限广阔的液体中运动时,由斯托克斯定律可得出小球在液体中受到的黏滞阻力 f为

当小球所受重力、浮力和黏滞阻力平衡时,小球在液体中匀速下落,由此可以解得液体的黏度η与小球匀速下落的速度(终极速度)的关系为

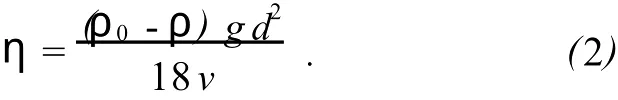
式中 d为小球直径,ρ0为小球密度,ρ为液体密度,v为小球的终极速度,g为重力加速度.

本实验中,由于小球是在直径为 D、液体深度为 h的玻璃管中下落,液体在各方向上无限广阔的条件并不能满足.因此,考虑管壁对小球运动的影响[2],黏度η的表达式修正为

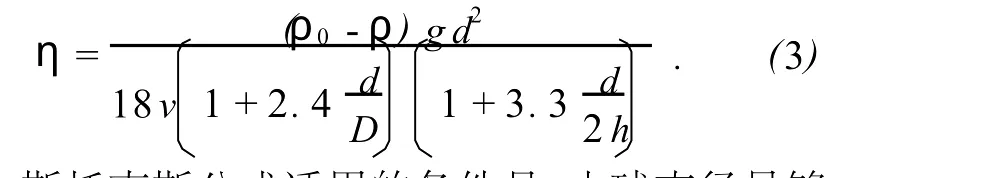
同时,斯托克斯公式适用的条件是:小球直径足够小[3],小球速度也很小,液体中不产生涡流,即要求雷诺数 Re很小.若 Re不是很小,液体运动状态的影响不能忽略,引入 Re对(1)式修正为

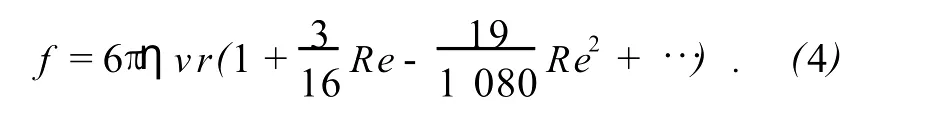
相应地对(3)式也加以修正,一般情况下:

1)当 Re＜0.02时,即小球直径和速度都很小,可以不予修正,(3)式的计算结果即为黏度的零级近似值η0.

2)当0.02＜Re＜0.5时,可以进行一级修正,经一级修正后黏度η的近似值为

3)当 Re＞0.5时,必须进行二级修正,经修正后黏度η的近似值为

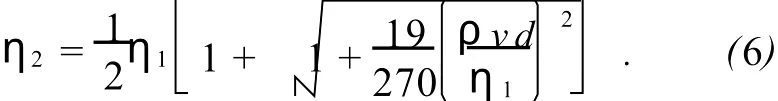
处理实验数据时,由式(3)得出η0后,必须对Re验算,确定它的范围并对η0进行修正,以得到符合实验要求的黏度值.而开展黏度测量实验的关键在于能否精确测量小球的终极速度v.

在本实验系统中,应用超声波的多普勒效应测量小球的终极速度v.落球装置如图1所示,超声波发射器和接收器安装在玻璃管的底部,超声波发射器向液体中下落的小球发射超声波,下落运动中的小球再将超声波反射至接收器,接收器接收的反射信号频率 f″与发射信号频率f将不同,其差值(f″-f)即为多普勒频移Δf[4].

图1 落球装置

若待测液体中的声速为 u,发射信号频率为f,则下落过程中的小球接收信号的频率 f′为

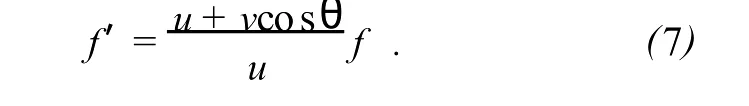
接收器接收到的落球反射信号的频率 f″为

则接收器接收信号与发射信号间的频移Δf为

因为 v cosθ≪u,(9)式可简化为

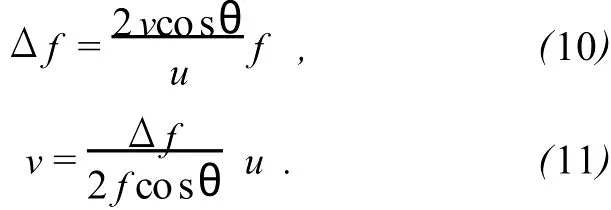
式中θ为接收器接收信号与小球下落速度之间的夹角,它随小球位置的不同而变化,cosθ值为

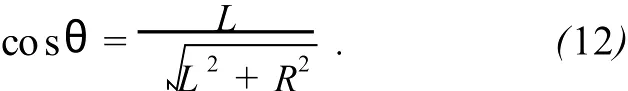
式(12)中 R已知,L可由玻璃管外壁上的A,B和C环线标记(即测量多普勒频移Δf时小球的位置)测得.将由式(11)计算的小球终极速度 v代入(3)式即可得出黏度的零级近似值η0.

3 实验系统

实验系统由玻璃管落球装置、信号发生器、超声波发射器、超声波接收器、信号接收电路和数据测量单元等组成.实验系统电原理如图2所示.

图2 实验系统电原理框图

3.1 玻璃管落球装置

将玻璃管固定在水平底座上,在玻璃管外壁上等距离刻画A,B和C 3条环线作为测量标记.液面至测量起点A标记线距离为所选小球达到终极速度时下落距离[S≈ρ0(ρ0-ρ)gd4/81η2]的2倍左右,以确保开始测量时小球匀速下落.在玻璃管的底部安装超声波发射器和接收器并密封,如图1所示.

3.2 数据测量单元

数据测量单元由多普勒频移信号处理电路和数字存储示波器组成,用于提取和测量经信号接收电路处理的超声波接收器接收信号的频移.实验系统中超声波中心频率为2 M Hz,波长短,能量集中,定位较准确[5],能探测到直径约2 mm的小球,同时超声波接收器接收信号的频率变化大,对比明显,实验成功率高,效果较为理想.

3.2.1 频移信号处理电路

实验系统采用的频移信号处理电路如图3所示,其中由四象限模拟乘法器AD835,R1和 R2构成混频电路,调节电位器 R2可微调电路的增益;由U 2A,R4,R5和 C1等组成有源低通滤波器;R6和C2组成 RC低通滤波器.

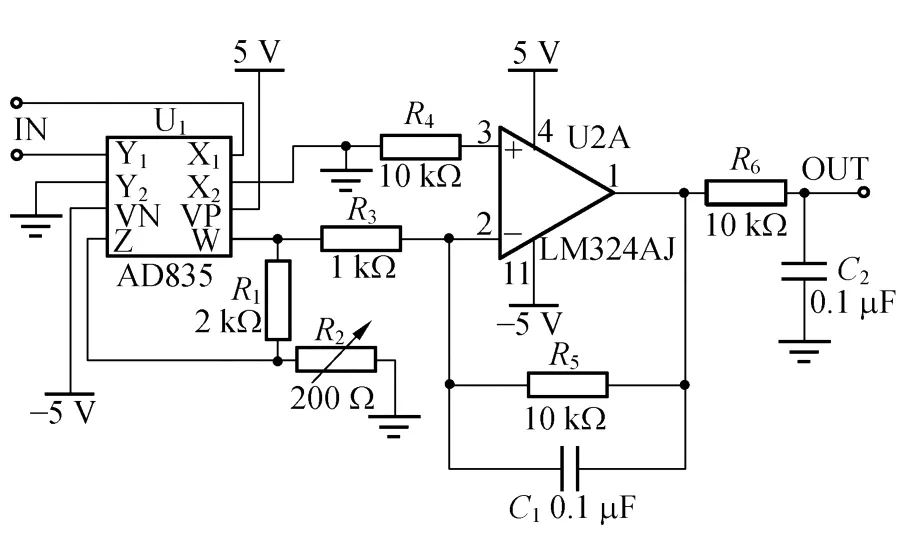
图3 频移信号处理电路原理图

若输入信号 x1=E1cos(2πf t+φ1),y1=E2cos(2πf″t+φ2),x2=y2=0,则 AD835 混频电路的混频输出为

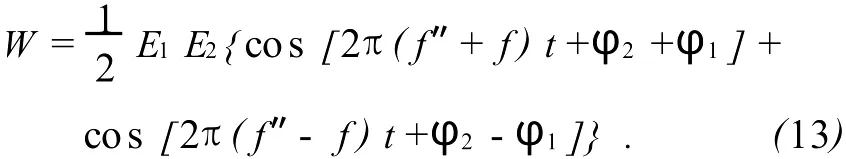
实验中,由信号源输出的激励信号(频率 f)分成2路:一路接至AD835的X1输入端;另一路接至超声波发射器,激励发射换能器连续向液体中下落的小球发射超声波,接收器接收小球反射回来的超声波(频率 f″)并将其转换为相应的电信号输送至信号接收电路,接收信号经接收电路放大、整形后接至AD835的 Y1输入端,从而对发射和接收电信号进行混频.AD835输出的混频信号经有源低通滤波器和 RC低通滤波器两级滤波,即可有效提取出混频信号中的差频成分

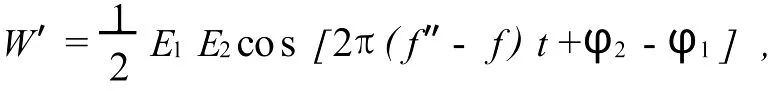
即多普勒频移信号[6],以供后续的数字存储示波器测量频移(Δf=f″-f).

3.2.2 频移测量

实验过程中,由于小球的下落时间有限,且多普勒频移随小球的位置不断变化,必须在其运动过程中及时将相关测量位置的频移信号波形储存,以便后期分析计算,所以本设计选用数字存储示波器作为频移信号的存储和测量设备.数字存储示波器采用高分辨率的A/D变换器,使其能够在示波器屏幕上显示波形的同时还能显示有关参量,且该示波器采用光标进行数字化测量,可大大减小人为误差以及放大器与示波管的非线性对测量精度的影响,因此由数字存储示波器显示的波形和测量数据比通用的电子示波器精度要高.

当小球经过玻璃管外壁上 A和C环线标记时,分别按动数字示波器面板上的“RUN/STOP”触发控制按钮,即可控制数字示波器采集并存储小球由A至C过程中频移信号处理电路输出的频移信号.通过分析频移信号波形的起点、中点和终点,即可计算出小球经过 A(起点),B(中点)和 C(终点)相应位置时对应的多普勒频移Δf,实现1次抛球测量多组数据,以提高测量精度和测量速度.

4 实验内容及方法

本实验系统可测量液体黏度,还可开展超声测速、多普勒效应验证以及超声测距等多项与多普勒效应相关的综合性、设计性实验.

4.1 测量液体黏度

1)调整玻璃管落球装置底盘以达到水平状态,并在玻璃管中装入适量的待测黏性液体.

2)用标准刻度尺分别测量 A,B和C环线标记与玻璃管底部超声波发射接收器之间的距离L,用于式(12)计算cosθ值.

3)调整好数字存储示波器,沿玻璃管中轴线释放小球,当小球经过玻璃管上 A环线标记时,按动数字示波器面板上的“RUN/STOP”触发控制按钮,控制数字示波器开始采集频移信号处理电路输出的频移信号;当小球经过玻璃管上 C环线标记时,再按动数字示波器面板上的“RUN/STOP”触发控制按钮,控制数字示波器停止采集,存储已采集的频移信号.分析存储的频移信号波形,分别计算出小球经过 A(起点)、B(中点)和 C(终点)相应位置时对应的多普勒频移Δf.

4)由液体中的声速 u、发射频率 f和接收信号的频移Δf,应用式(11)分别计算小球的下落速度v,然后利用式(3)即可计算液体黏度的零级近似值η0.

5)计算雷诺数 Re,并根据雷诺数的大小,对η0进行相应的修正.

4.2 测量液体内物体运动速度,验证多普勒效应

利用数据测量单元测量小球匀速经过玻璃管外壁上不同环线标记时接收信号的频移.由液体中的声速 u、发射频率 f和接收信号的频移Δf,利用式(11)可计算小球的下落速度 v;然后利用相同温度下液体的已知黏度,应用式(3)又可计算相同条件下小球的终极速度 v′,v与v′相比较,既可验证多普勒效应公式,同时又可直观地说明超声波多普勒测速原理.

5 实验结果

测量20.0℃时测量蓖麻油的黏度η数据:小球直径d=1.997×10-3m,小球密度ρ0=7.85×103kg/m3,蓖麻油密度ρ=9.58×102kg/m3,玻璃管内径 D=5.966×10-2m,液体深度 h=0.202 0 m;20.0℃时蓖麻油黏度的公认值η′=0.950 Pa·s,蓖麻油中的声速 u=1 200 m/s.η的6次测量结果为0.961,0.960,0.960,0.962,0.961,0.960 Pa·s,¯η为0.961 Pa·s.

实验结果表明,利用本实验系统测得的蓖麻油黏度与相同温度下蓖麻油黏度的公认值比较,测量值的相对不确定度在1.2%以内,因为1次抛球可连续测量3组数据,使得测量结果重复性好,可信度高.

6 结束语

利用本文介绍的实验系统,可以开展多项综合性、设计性实验.由于使用数字存储示波器进行相关数据的测量,使波形测量的精确度提高,减少了测量误差;同时又可以加深学生对数字存储示波器工作原理的理解和认识,进一步熟悉数字存储示波器的基本操作和使用方法.实验中信号的传输、转换和测量过程清晰明了,利于学生在实验过程中细致观察物理过程,分析测量误差的来源.通过实验可拓展学生的思路,以培养学生的综合实验能力和创新能力.此实验系统结构简单,无需复杂的软件编程,各实验室均可以自行完成制作[7].

[1] 王丽娟,张平.探究落球法测液体黏度实验中小球达匀速运动所需的时间[J].物理实验,2009,29(1):37-39.

[2] 任新成,王玉清,安爱芳.多管落球法测液体黏度实验的研究[J].物理实验,2004,24(4):35-37.

[3] 郑勇林,杨晓莉,杨敏.落球半径对测量黏度的影响[J].物理实验,2003,23(9):42-44.

[4] 姚运萍,陈继开,孙岳中一.超声波多普勒黏度检测仪[J].仪表技术与传感器,2008,(3):18-20.

[5] 郭敏.一种测量液体粘滞系数的新方法[J].物理,2001,30(4):220-222.

[6] 李翔,徐平,Bottineau P.基于乘法器的超声多普勒实验仪的研究[J].大学物理,2008,27(7):53-55.

[7] 李光仲,刘俊英,王云创,等.声速测量实验装置扩展应用[J].物理实验,2006,26(2):35.