如何判定物体做简谐振动
2010-01-26孔若平
孔若平
( 西北工业大学启迪中学 陕西 咸阳 710072)
如何判定一个振动系统是否做简谐振动,一般可以用以下两种方法.
动力学特征:F=-κx,即如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,那么质点的运动就是简谐振动.
振动图像法(x-t图像):x=Asin(ωt+φ) 用x代表质点相对于平衡位置的位移,t代表时间,即如果质点的位移与时间的关系遵从正弦(或余弦)函数的规律,它的振动图像x-t是一条正弦曲线,这样的振动就是简谐振动.
现行教科书及各类参考书对简谐振动的判据说法不一,笔者认为动力学方法在高中阶段对学生比较适用,简单步骤如下.
(1)确定振动的平衡位置,物体停止振动静止时的位置即为平衡位置,并且规定正负方向.
(2)在振动过程中任选一位置(平衡位置除外),对物体进行正确的受力分析.
(3)对物体所受的力沿振动方向进行分解,求出振动方向上的合外力.
(4)判定振动方向上的合外力与位移的关系是否符合F=-κx.
【例1】证明竖直悬挂弹簧的运动是简谐振动.
证明:弹簧下端悬挂的物体m竖直方向振动时,回复力由重力和弹力的合力提供.设弹簧的劲度系数为κ,在平衡位置时,回复力F=0,此时弹簧伸长为x0,则
κx0-mg=0
(1)
以平衡位置为坐标原点,设向下为正方向,建立坐标轴,如图1所示.当物体在振动中到达任意点x时,其回复力为
F=mg-κ(x+x0)
(2)
由(1)、(2)式得
F=-κx
可见物体受的回复力跟偏离平衡位置的位移的大小成正比、方向跟位移方向相反,即该物体做简谐运动.
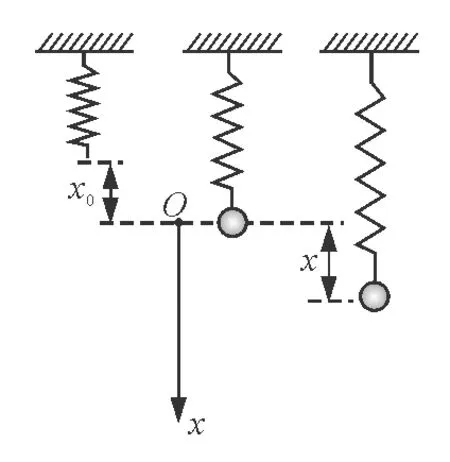
图1
【例2】如图2(a)所示,在一倾角为θ的光滑斜板上,固定着一根原长l0的轻质弹簧,弹簧另一端连接着质量为m的滑块,此时弹簧被拉长为l1.现把滑块沿斜板向上推至弹簧恰好为原长,然后突然释放.求证滑块的运动为简谐振动.
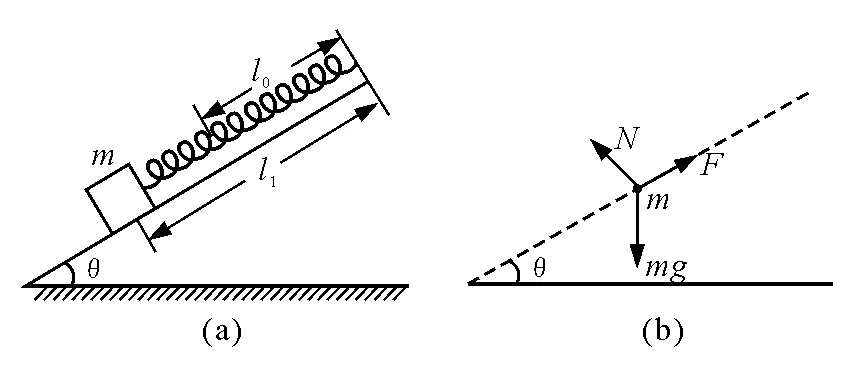
图2
证明:松手释放,滑块沿斜板往复运动——振动.而振动的平衡位置即滑块开始时静止(合外力为零)的位置,在平衡位置(即弹簧长为l1)处,弹簧弹力等于重力沿斜面向下的分力,即
mgsinθ=κ(l1-l0)
滑块离开平衡位置受力分析,如图2(b)所示.滑块受三个力作用,其中弹簧弹力和重力沿斜面向下的分力的合力提供回复力.偏离平衡位置x(设沿斜面向上为正方向,向下为负方向)时,弹簧伸长量
Δx=(l1-l0)-x
此时沿斜面方向的合力为
F=-mgsinθ+κ[(l1-l0)-x]=-κx
方向沿斜面向下,即
F=-κx
可见滑块受的回复力跟偏离平衡位置的位移的大小成正比、方向跟位移方向相反,即该物体做简谐运动.
【例3】 如图3(a)所示,木块质量为m,放在水面上静止(处于平衡状态).现用力向下将其压入水中一段深度后撤掉外力,木块在水面上下振动,试判别木块的振动是否为简谐振动.

图3
证明:以木块为研究对象,设静止时木块浸入水中Δx深.当木块压入水中x后所受力如图3(b)所示,则
F=mg-F浮
(1)
又F浮=ρgs(Δx+x)
(2)
由(1)式和(2)式得
F=mg-ρgS(Δx+x)
(3)
因为
mg=ρgSΔx
所以
F=-ρgSx
即
F=-κx(κ=ρgS)
可见木块受的回复力跟偏离平衡位置的位移的大小成正比、方向跟位移方向相反,即该物体做简谐运动.
实际在判断一个系统是否做简谐振动时,不仅要看系统中振动物体所受的是与其位移x成正比反向的线性回复力,同时还要看系统的机械能是否守恒.因此学生必须把系统的受力情况和机械能的情况联系起来综合考虑.
