不同龄期混凝土收缩徐变对三塔结合梁斜拉桥的影响
2010-01-25刘沐宇
刘沐宇, 程 涛
(武汉理工大学 道路桥梁与结构工程湖北省重点实验室, 湖北 武汉 430070)
近年来,由于钢-混凝土结合梁具有自重轻、强度高、刚度大等特点,在我国桥梁建设的应用中日趋广泛[1]。在建的武汉二七长江大桥是主梁采用钢结构,桥面板为混凝土结构,主梁与桥面板用剪力件连接的世界上最大跨度的三塔结合梁斜拉桥。钢-混凝土结合梁是由性质不同的两种材料结合在一起的整体结构,由于混凝土的收缩徐变影响,将在钢和混凝土的结合面上产生相互作用力,导致内力重分布,并致使结构产生大量的附加变形[2]。混凝土收缩徐变是随时间变化的,导致不同龄期的混凝土引起的效应有很大的区别,很多结合梁桥为了防止混凝土收缩徐变产生过大的挠度和应力变化,采用将预制混凝土板放置若干时间再进行架设的方法。因此,研究不同龄期混凝土收缩徐变对结合梁斜拉桥的影响效应,可以给同类桥型的设计和施工提供参考。
混凝土收缩徐变对桥梁的不利影响,很早就引起了国内外学者和工程界的重视。由于试验工作的困难,在已有的关于混凝土收缩徐变效应分析的文献中,多采用理论分析和计算模拟。Salvatore推导了按龄期调整的混凝土模量计算式,并对计算参数取值的有效性进行了分析[2];吴冲等采用有效弹性模量法对大跨度结合箱梁斜拉桥的混凝土收缩徐变应力进行了计算分析[3];叶梅新等结合具体工程实例,采用有限单元法分析了由于徐变引起的应力重分布,并探讨了不同龄期混凝土弹性模量的取值[4]。尽管已经有很多学者对混凝土的收缩徐变效应进行了研究,但是对三塔结合梁斜拉桥有关收缩和徐变的研究还较少。
本文以武汉二七长江大桥为工程背景,建立全桥有限元模型,在建模时分别考虑混凝土板的加载龄期为28d、90d、180d、270d,分析了三塔结合梁斜拉桥在收缩徐变影响下的挠度及应力变化情况。同时,对不同龄期混凝土收缩徐变产生的影响效应进行讨论,计算表明将混凝土板放置180d后再进行架设可以有效地减小混凝土收缩徐变对三塔结合梁斜拉桥的影响,本文的分析结果可为三塔结合梁斜拉桥设计和施工提供参考。
1 工程概况
武汉二七长江大桥主桥结构为三塔双索面斜拉桥,全桥总长1732 m,详细布置为90 m+160 m+616 m+616 m+160 m+90 m,见图1。两边跨各设一个辅助墩,主梁纵向采用半漂浮体系,墩塔固结,中塔采用塔梁铰接,全桥共设斜拉索132对,标准节段索距在主梁上为13.5 m。桥塔为花瓶型钻石构造钢筋混凝土结构,主塔高度为206 m。
主桥桥面体系采用双工字型钢主梁与混凝土桥面板组合而成的结合梁桥面形式,见图2,两工字型钢主梁中心距30.5 m,主梁梁高2.935 m;横梁纵桥向间距4.5 m,横梁高度与钢主梁一致;混凝土板厚度为26 cm,为了减小收缩徐变对三塔结合梁斜拉桥的影响,该桥将混凝土板放置180 d后再采用栓钉与钢主梁连接。汉口及武昌岸主梁90 m边跨采用现浇混凝土梁,以增加梁体自重,避免边墩和辅助墩出现负反力。
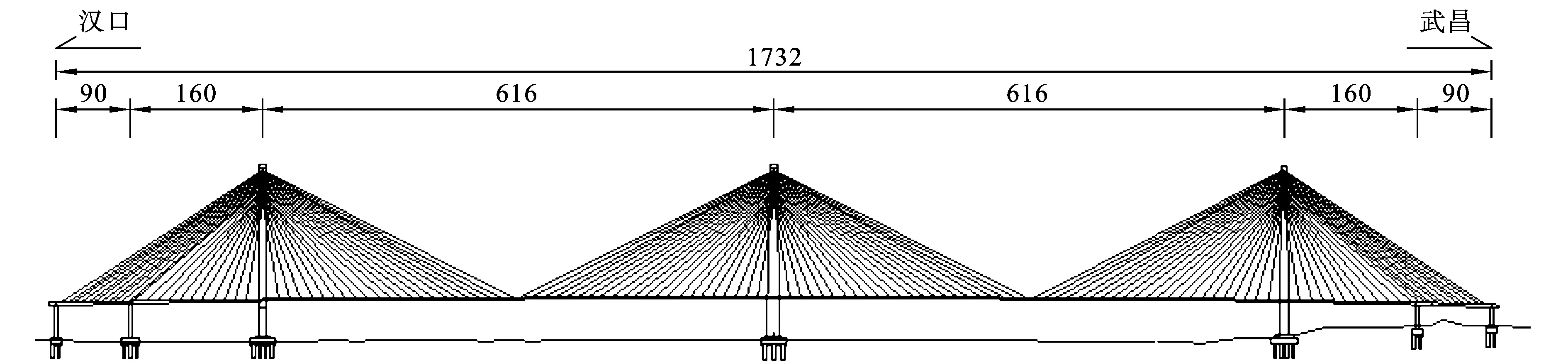
图1 二七长江大桥立面图(单位:m)

图2 钢-混凝土结合梁横断面图(单位:cm)
2 混凝土收缩徐变效应分析
2.1 全桥分析模型
按照桥梁实际结构尺寸,采用桥梁专业软件MIDAS/CIVIL建立有限元模型。主梁和塔采用梁单元,斜拉索采用桁架单元。主塔共有单元366个,结合梁主梁共有单元940个,混凝土主梁共有单元48个,每根斜拉索由塔上的节点和相应的主梁上节点连接而成的单个单元来构成,共132个单元。全桥共1486个单元,1362个节点。该桥的有限元模型见图3。

图3 全桥有限元模型
二七长江大桥的主梁有钢、混凝土两种材料,桥塔为混凝土,斜拉索为高强钢绞线,模型中各部分材料参数如表1。
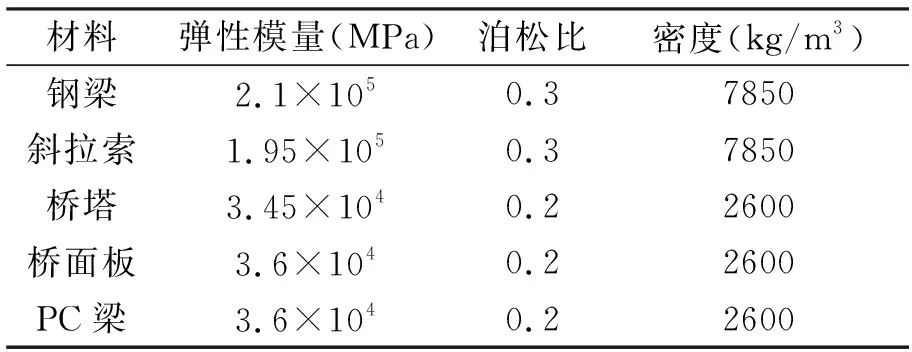
表1 材料参数
根据该桥设计思路,主桥施工共划分为79个施工阶段,其中每个标准梁段的施工流程为:
(1)用架梁吊装n号钢主梁、钢横梁及小纵梁;
(2)安装n号主梁对应的斜拉索,进行初张拉;
(3)安装预置桥面板,二次张拉n号主梁对应的斜拉索;
自2010年起,部分房地产估价机构先后开启了信息化探索之路,并取得了一定成果。主要分为两种类型:一类为独立运营,较为典型的有深圳世联、深圳国策、深圳评估中心、北京国信达等;另一类为联盟运营,较为典型的有中估联行、中房评、恒基数据、云估价、云房等。不管是独立运营,还是联盟运营,各房地产估价机构都致力于自动估价系统、知识管理系统、业务流程系统、自动办公系统、押品重估系统、不动产运营管理系统、投贷后资金管理服务系统等信息产品的开发与应用,以进一步提升传统业务服务效率和不断开拓新型业务发展空间,也对行业面临的现状困境起到了一定的改善作用。
(4)完成n号主梁安装,前移吊机,安装(n+1)号钢主梁、钢横梁及小纵梁。
本模型所考虑的荷载主要包括恒载、二期恒载、活载和温度荷载,其中恒载包括自重、拉索初拉力与基础沉降,活载按公路一级设计,按照《公路桥涵设计通用规范》(JTG D62-2004)的相关规定进行组合。
2.2 收缩徐变效应分析
在混凝土收缩分析中,由于混凝土收缩与构件内部应力无关,只是关于时间的函数。混凝土收缩引起的应变可以表示为
εcs(t,ts)=εcs0βs(t-ts)
(1)
其中,εcs0为名义收缩系数,βs为收缩随时间发展的函数。
在三塔结合梁斜拉桥分阶段施工过程中,混凝土的徐变系数随着时间发展不断变化,因此,在进行徐变分析时,采用叠加法模拟施工过程可以得到较为精确的结果,但是会导致计算过程非常复杂,需要借助有限元软件进行辅助计算[5]。
混凝土徐变应力与应变本构关系为:
(2)
其中,ε(t)为混凝土总应变,σc(t0)为混凝土应力,E(t0)为混凝土弹性模量,C(t,t0)为混凝土徐变度,其表达式为:
(3)
式中,φ(t,t0)是加载龄期为t0,计算考虑龄期为t时的徐变系数。
根据我国现行的《公路桥涵钢筋混凝土及预应力钢筋混凝土设计规范》(JTG D62-2004),混凝土徐变系数可按下列公式计算:
φ(t,t0)=φ0βc(t-t0)
(4)
其中,εcs为名义徐变系数,βc为加载后徐变随时间发展的系数。
依据线性徐变理论,采用叠加原理,式(2)可以表示为:
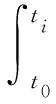
(5)
图4~8以及表2给出了武汉二七长江大桥成桥阶段和正常运营阶段主梁挠度、塔顶水平位移、桥面板以及钢主梁上、下缘应力情况。
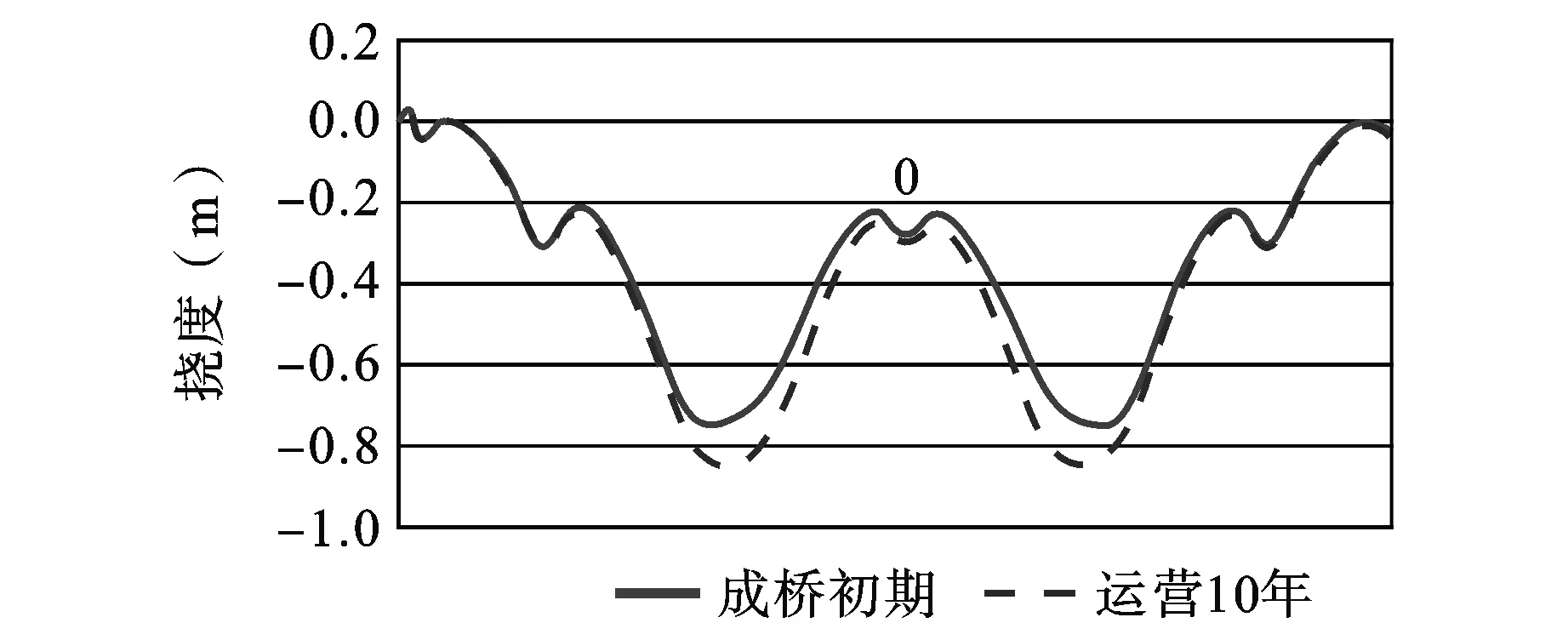
图4 主梁挠度曲线
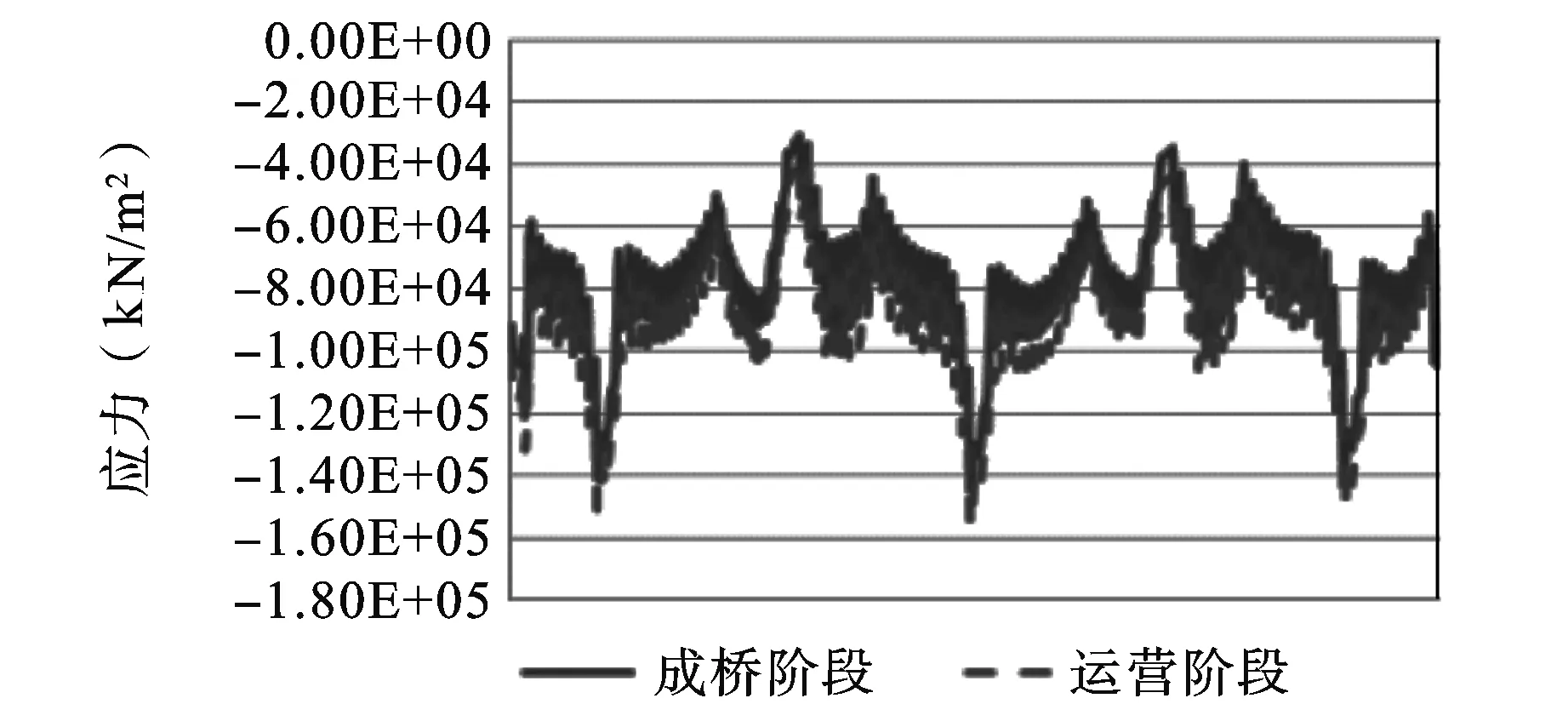
图5 钢主梁上缘应力
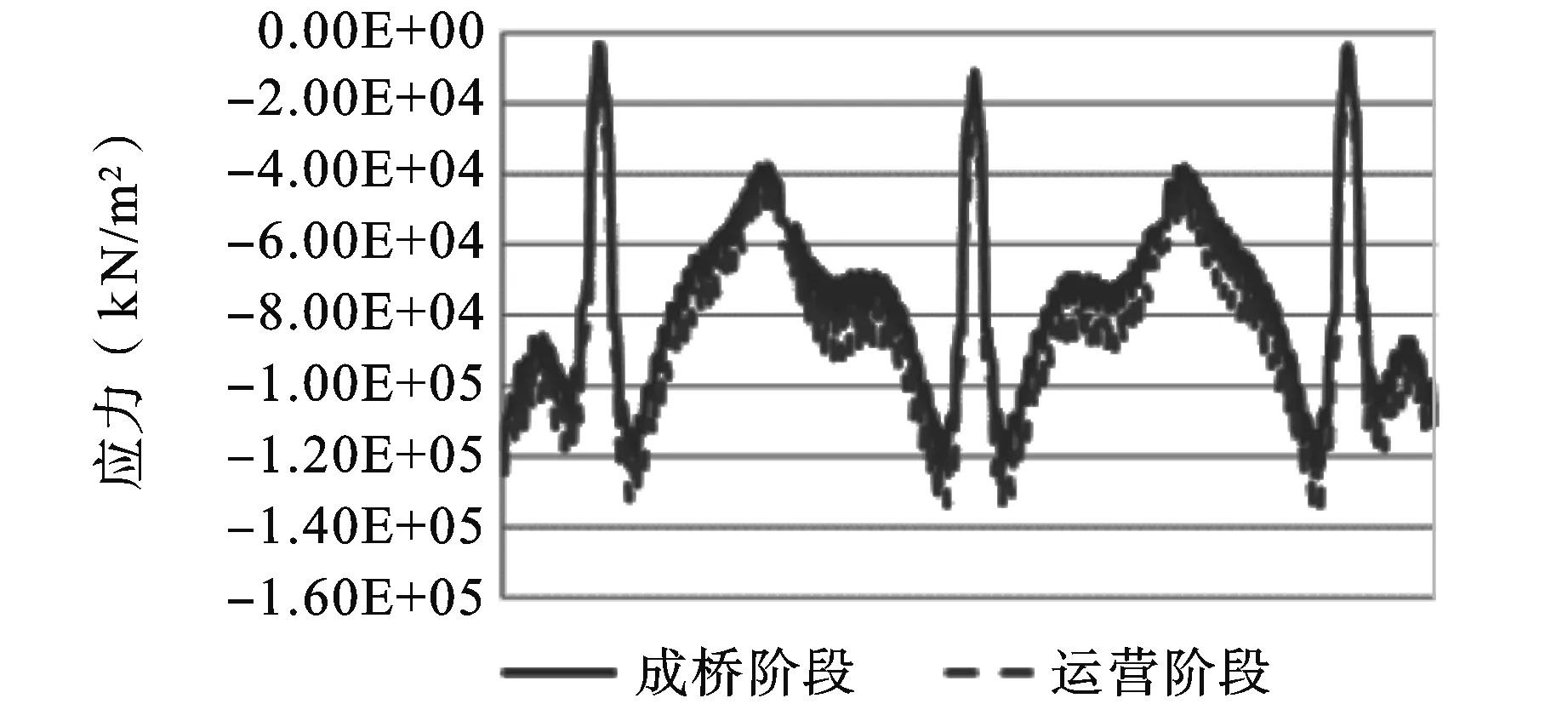
图6 钢主梁下缘应力
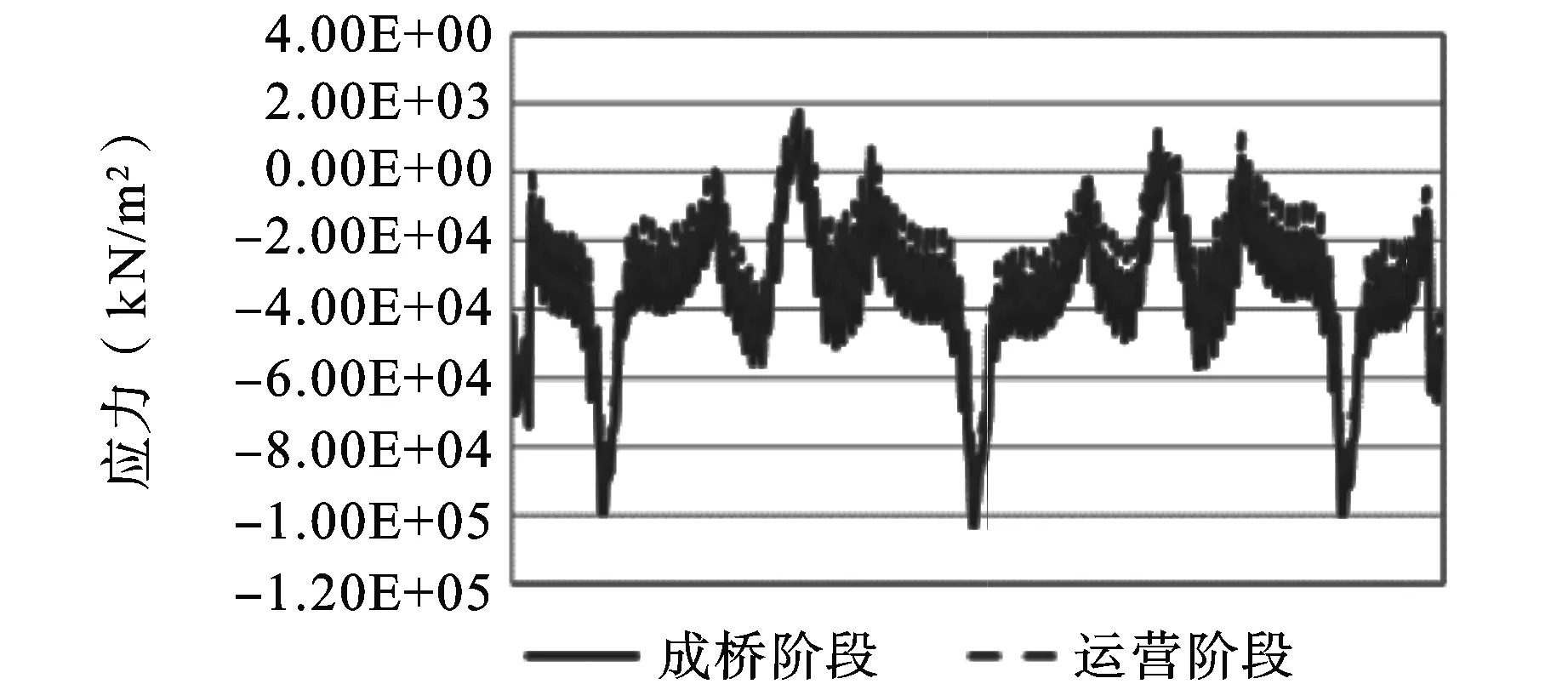
图7 混凝土板上缘应力

图8 混凝土板下缘应力
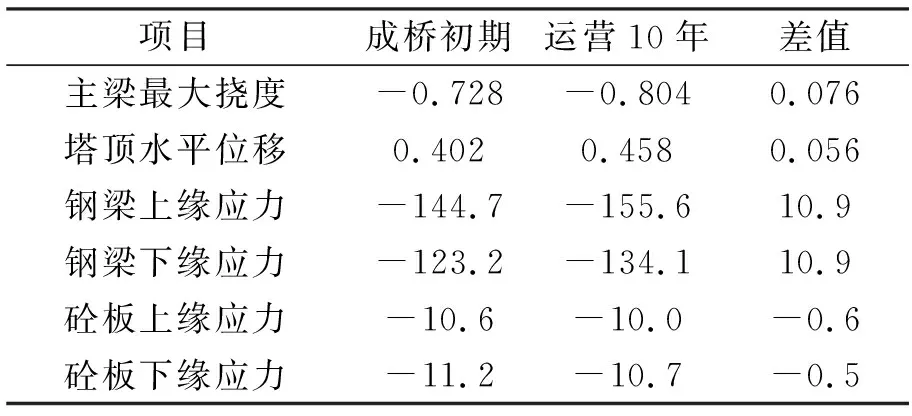
表2 挠度与应力计算结果
从图4~8以及表2中可以看出,结合梁主梁的挠度明显增大,达到了7.6 cm,塔顶的水平位移也增大了5.6 cm;混凝土板的压应力变化不是很明显,只降低了0.6 MPa,相对于混凝土应力减小而言,钢主梁压应力变化比较明显,增加了10.9 MPa。
2.3 不同龄期混凝土收缩徐变影响效应对比分析
由于时间的变化,混凝土强度不断提高,尤其是对于高强度混凝土而言,其内部组织结构很快会变密实,随着加载龄期的增大,徐变变形快速减小,由于混凝土收缩徐变所产生的效应也会随之变小。
为了研究不同加载龄期的混凝土对三塔结合梁斜拉桥的影响,在施工阶段建模过程中,分别定义混凝土板加载龄期为28 d、90 d、180 d和270 d,选取我国《公路桥涵钢筋混凝土及预应力钢筋混凝土设计规范》,根据规范中的公式软件自动计算混凝土徐变系数随时间的变化,从而得到不同龄期混凝土板对三塔结合梁斜拉桥的影响效应。图9~13分别给出了不同加载龄期的混凝土桥面板收缩徐变对三塔结合梁斜拉桥主梁挠度以及应力的影响。
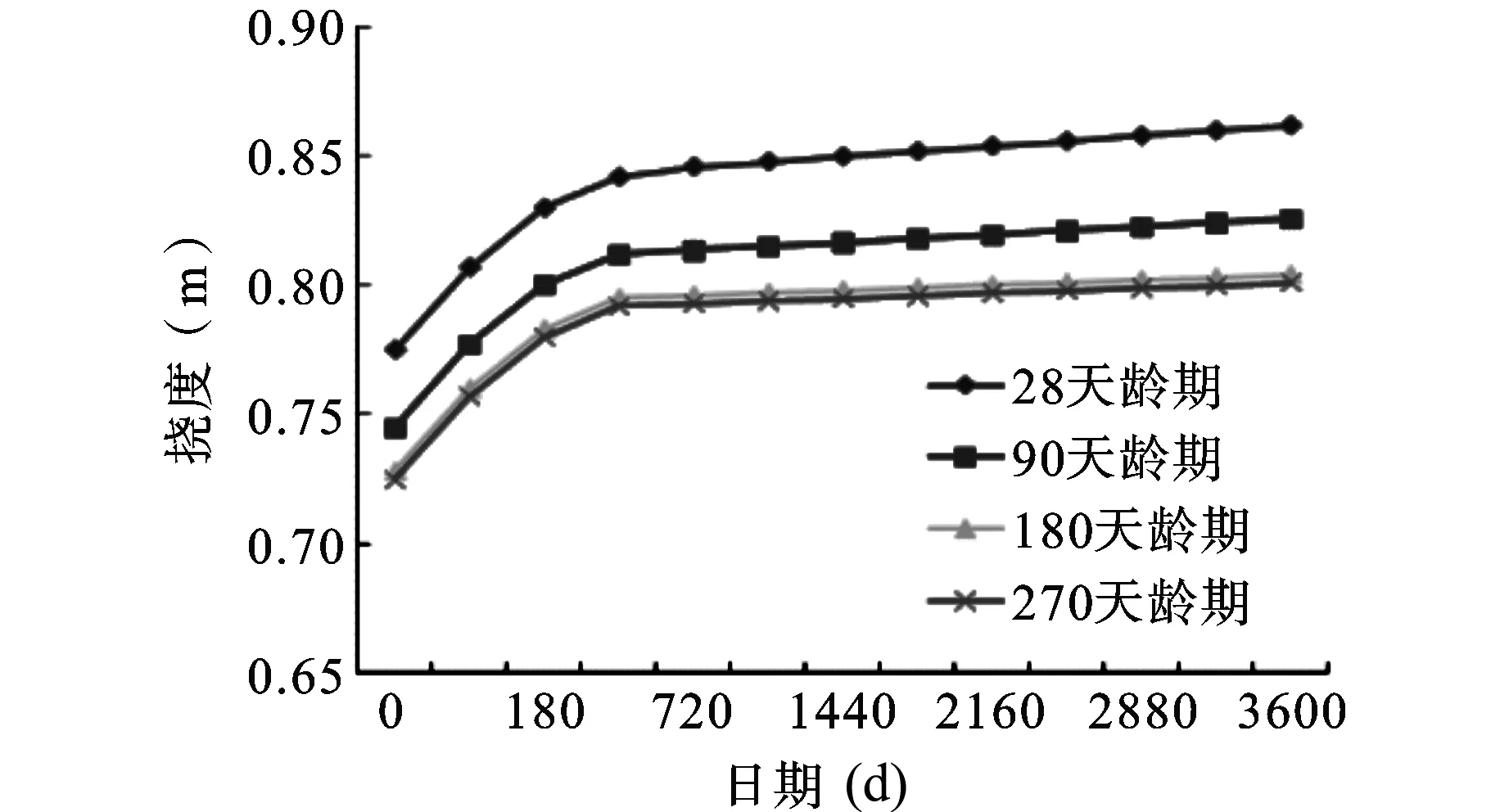
图9 主梁最大挠度
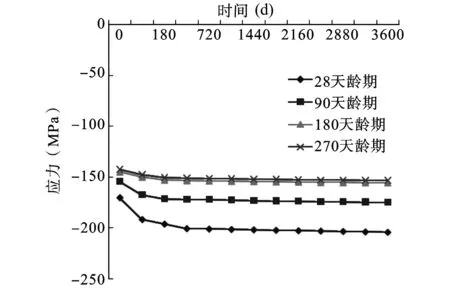
图10 钢主梁最大上缘应力
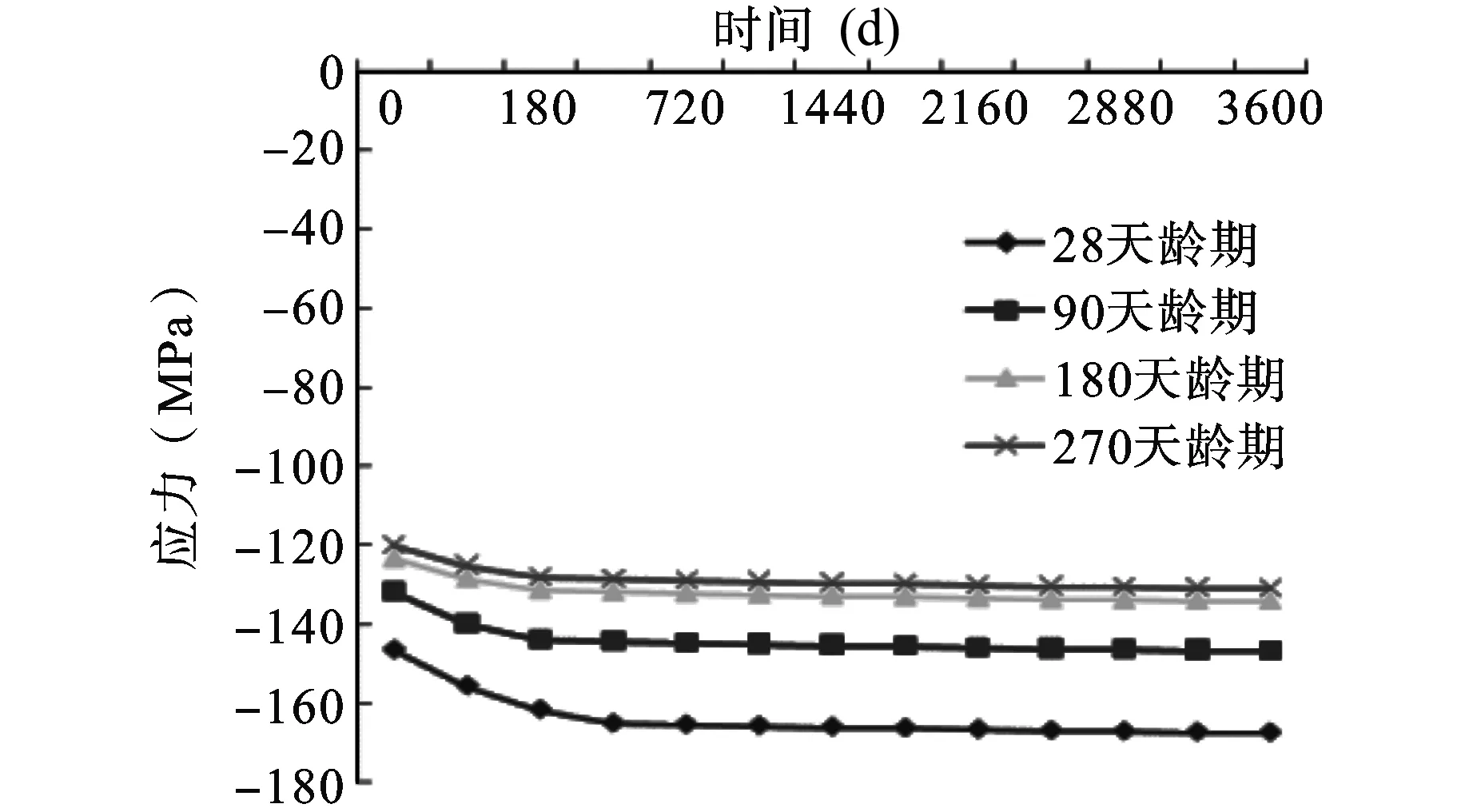
图11 钢主梁最大下缘应力
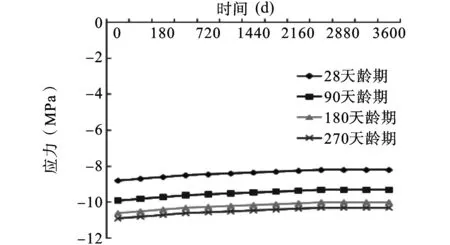
图12 混凝土板最大上缘应力
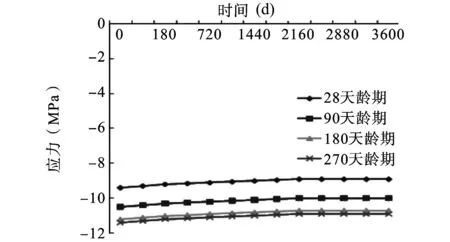
图13 混凝土板最大下缘应力
由图9~13对比分析可以看出,由于加载龄期的不同,混凝土收缩徐变所产生的效应也是不同的。加载龄期越长,引起的挠度变化越小,钢主梁以及混凝土板的应力变化也越小。但从28 d龄期,90 d龄期,180 d直到270 d龄期的混凝土来看,收缩徐变对结合梁斜拉桥影响减小的趋势也越来越小,尤其是180 d和270 d龄期的混凝土相比,基本已经没有变化,趋于稳定。因此,武汉二七长江大桥在施工过程中将预制混凝土板放置180 d后再进行架设,可以有效地预防混凝土收缩徐变对结合梁斜拉桥挠度和应力的影响。
3 结 论
(1)混凝土收缩徐变效应引起主梁竖向挠度增大,塔顶水平位移也相应增大。在混凝土收缩徐变的影响下,二七长江大桥的主梁挠度增大7.6 cm,塔顶的水平位移增加5.6 cm。
(2)混凝土收缩徐变对混凝土桥面板的应力影响不大;相对于混凝土板而言,钢主梁应力影响较为显著。在二七长江大桥中,由于混凝土的收缩徐变,混凝土桥面板压应力减小0.6 MPa,钢主梁拉应力增量达到了10.9 MPa。
(3)混凝土加载龄期越长,产生的收缩徐变效应越小,但当混凝土龄期达到180 d时,对三塔结合梁斜拉桥挠度和应力的影响已经趋于稳定。因此,在武汉二七长江大桥的施工中,将混凝土桥面板放置180 d后再进行架设,可以有效地减小收缩徐变对三塔结合梁斜拉桥的影响,是合理的,可以为同类桥型的设计与施工提供参考。
[1] 雷自学, 晏兴威, 董三升. 混凝土收缩徐变效应对曲线钢-混凝土箱型结合梁桥的影响[J]. 长安大学学报(自然科学版), 2008, 28(5): 77-80.
[2] 邱文亮, 姜 萌, 张 哲. 钢-混凝土组合梁收缩徐变分析的有限元方法[J]. 工程力学, 2004, 21(4): 162-166.
[3] Slavatore G M, Claudio M. Preflex beam: a method of calculation of creep and shrinkag[J]. Journal of Bridge Engineering, ASCE, 2006, 11(1): 48-58.
[4] 吴 冲, 曾明根. 大跨度组合箱梁斜拉桥混凝土收缩与徐变应力分析[J]. 世界桥梁, 2004,(s1): 37-41.
[5] 黄 琼, 叶梅新, 韩衍群. 钢-混凝土叠合板桥面的徐变和应力重分布研究[J]. 铁道科学与工程学报, 2006, 3(3): 15-20.
[6] 陈明宪, 彭建新, 颜东煌,等. 按龄期调整的有效弹性模量法分析混凝土收缩徐变[J]. 长沙交通学院学报, 2004, 20(3): 16-19.
