波前相位差法探测器的设计

于学刚，刘 忠，金振宇，杨 磊

(中国科学院国家天文台云南天文台，云南 昆明 650011)

利用望远镜对天文目标成像时，由于大气湍流及望远镜像差的影响，会造成波前失真。波前相位差法[1]是基于相位差法的一种相位复原和图像复原技术，主要是利用在焦面和离焦面位置上同时采集的一对图像，对光瞳上的波前相位分布进行恢复，同时也可以对目标进行恢复。波前相位差法具有采集光路简单、可以探测分离光瞳间波前的整体涨落(piston)误差、采集图像量不大、可用于扩展光源探测[2]等诸多优点而被广泛应用。

探测器是实现波前相位差法的重要组成部分，设计合理的探测器会提高复原结果的信噪比。目前常见的波前相位差法探测器主要有利用棱镜分像[3]将两个图像分别成在两个CCD上，或者采用多个棱镜利用分光和反射镜的配合[4]将两个图像成在同一个CCD上。前者虽然光路简单，但需要两个CCD，增加了探测器的成本(增强型CCD价格不菲)。后者采用多个棱镜，保证了两个图像的同步、实时，还可以自由控制离焦量和两个图像的间距进而应用于不同的望远镜终端。但棱镜较多，光路较复杂。

本文提到的相位差法波前探测器是指在对偏振特性不明显的目标进行探测时，可以利用晶体的偏振原理，将一个图像分成两个，因为e光(非寻常光)和o光(寻常光)折射率不同，两者在同一介质中传输时存在光程差[5]，这样自然获得了焦点像和离焦像，通过合理的结构参数设置也得到了合适的离焦量(焦面像和离焦像之间的距离)。利用这种方法设计的波前相位差法探测器，光学系统结构简单，并将焦点像和离焦像同时成在一个CCD上，保证了采集图像的同步、实时、图像的强度相当，降低了由探测系统引起的误差。

1 波前相位差法探测的理论分析

在做波前相位差法探测时，离焦量是进行相位迭代的一个重要参量，这一参量由(1)式[6]给出：

(1)

其中，Δz为离焦量；δ为离焦面图像波前失真产生的P-V值(peak-to-valley)；F为望远镜的有效焦距；M为对焦点像和离焦像进行放大的物镜放大倍率(物镜把焦面像和离焦像放大后成在同一个CCD上)；D为望远镜口径。一般情况下要求δ取0.8～1[7]，这样复原的结果较为理想。

而离焦像差对应于泽尼克多项式的第4项，即:

(2)

其中，A4为泽尼克第4项系数(单位为波长λ)；ρ为单位径向坐标。则离焦像差与离焦面图像波前失真产生的P-V值δ满足下面的关系式：

(3)

由上面的关系，知道泽尼克多项式的离焦系数A4是一个依赖于离焦图像的离焦距离Δz,望远镜的口径D和理想焦长F的函数即：

(4)

其中，λ为工作波段的中心波长。从这一公式知道，在望远镜的口径和焦长确定以后，Δz和A4是对应的。这样在利用晶体偏振特性来设计波前相位差法探测器时，可以通过光学设计软件给出的泽尼克系数A4的大小来判断所需的离焦量是否满足要求。

2 波前相位差法探测器的光学设计

本系统是利用晶体的偏振特性完成分像，获得合适的离焦量，并将两个图像成在同一个ICCD(Intensified Charge Coupled Device)上，同时要保证两个图像相互间距离合适(要根据CCD版面尺寸来确定)，还要保证焦点像和离焦像的像差不大。利用ICCD短曝光获得斑点图，再对光瞳的波前相位进行恢复或者对目标进行恢复。

2.1 晶体的双折射

常见的波前相位差法探测器采用棱镜分光的方式来获得焦面像和离焦像，本设计利用晶体的偏振原理[8]来实现。当一束光在各向异性晶体的界面折射时，一般可以产生两束折射光，一束为e光(非寻常光)，一束为o光(寻常光)见图1，并且两者以一定的角度分开。如果入射光是一束会聚光束，在焦面的位置，就可以自然获得焦点像和离焦像[4-5](图2)。

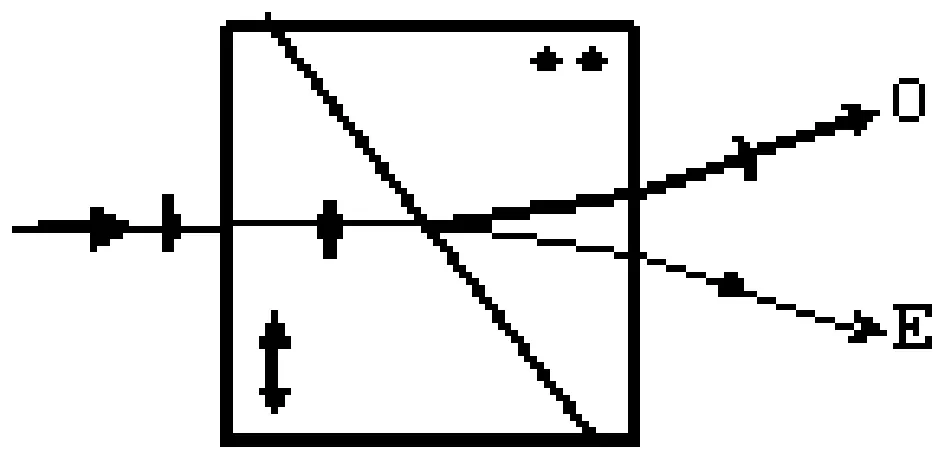
图1 晶体的双折射

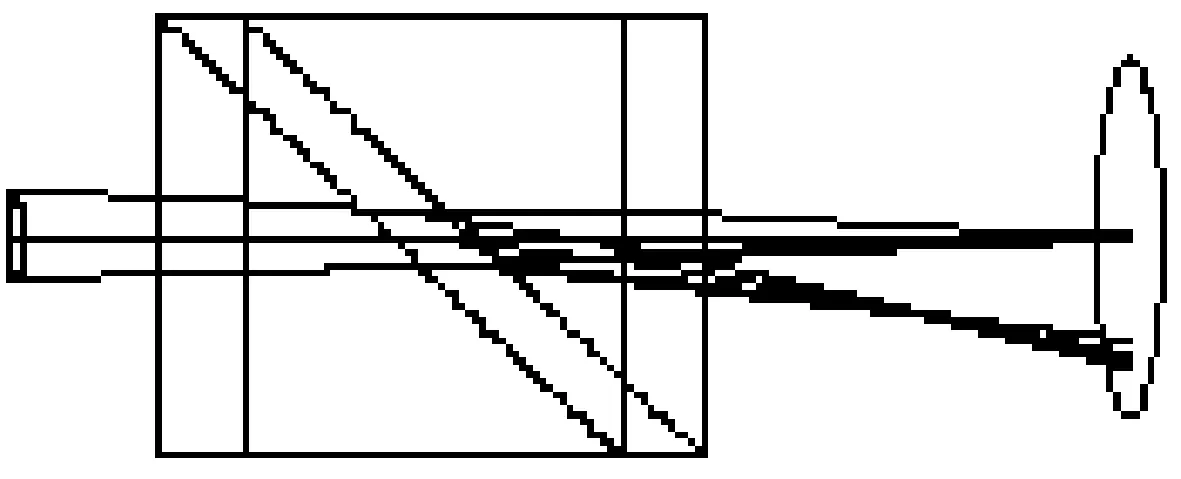
图2 会聚光线的双折射

焦点像和离焦像分开的角度与光轴的方向、晶体的厚度以及晶体通光表面的倾斜角度有关。离焦量的大小主要与ne(e光的折射率)和no(o光的折射率)的差值大小ne-no、晶体的厚度、晶体表面的倾斜角度有关。

2.2 光学系统结构参数

光学设计的重要目的是分像和满足离焦量，即泽尼克系数的第4项P-V值在0.8～1个波长[9]。晶体的厚度和通光面的表面倾斜与离焦量有着重要的关系，通过合理选择晶体的厚度及表面的倾斜角度就可以获得需要的离焦量。下面以云南天文台口径为1m望远镜为例设计波前相位差法探测器。云台1m望远镜的参数为口径D=1.06m，有效焦距F=13.3m，波长取可见光中心波长λ=550nm。将采用ICCD采集图像，为了满足采样定理，需要用物镜将焦面像和离焦像放大7倍左右，成像在ICCD上。由(1)式求得所需离焦量为:

Δz=29.8895 mm

此时，对应的P-V值为0.8806λ。

这样的一个离焦量主要由两部分产生，一部分是由e光和o光在晶体中的光程差产生，由晶体的厚度决定即：

Δz2=|ne-no|d

(5)

另一部分由晶体通光面的倾斜来产生，可以通过改变晶体通光表面的倾斜角度看出对泽尼克第4项系数(离焦)的影响，来获得所需要的离焦量。但获得离焦量的同时也会引入像差，其中较大的像差为像散，也存在色散，合理地选择倾斜角度是重要的。这样即能获得需要的离焦量，同时可以降低像散，又可以防止因为倾斜角度过大而产生较大的像差, 影响复原结果的精度。图3是光学系统示意图。

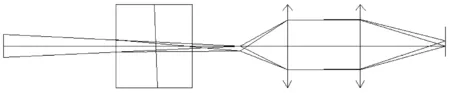
图3 波前相位差法探测器光路

为了满足所需离焦量，需要选择|no-ne|较大的晶体，方解石是较为合适的晶体。具体的参数设置为：晶体通光口径为10mm×10mm，厚为6.3mm,为了使两个图像距光轴等距离分布，晶体出射光的表面有8.3°的倾角。在晶体出射光的表面，有一个同等倾斜角度的玻璃，配合晶体降低像散。之后再经过物镜(物镜起放大作用)成像在ICCD上，PD波前探测器用于其它焦长和口径的望远镜上时，可以通过在CCD前的离焦像或焦面像的其中一个光路中加入平板玻璃来调节离焦量，满足不同的离焦距离。

2.3 光学系统评价

波前相位差法探测器的重要目的就是获得合理的离焦量，同时像差要控制在一定范围之内，本设计最终获得的因为离焦量产生的波前失真P-V值为0.8806λ。此时焦点像的像差和离焦像的像差是不同的，焦点像的像差很小，相当于在会聚的光路中放入一个厚度为6.3mm的平板玻璃产生的像差。另一部分为离焦像的像差，这里列出由光学设计软件给出的波长为550nm时的赛德系数见表1。

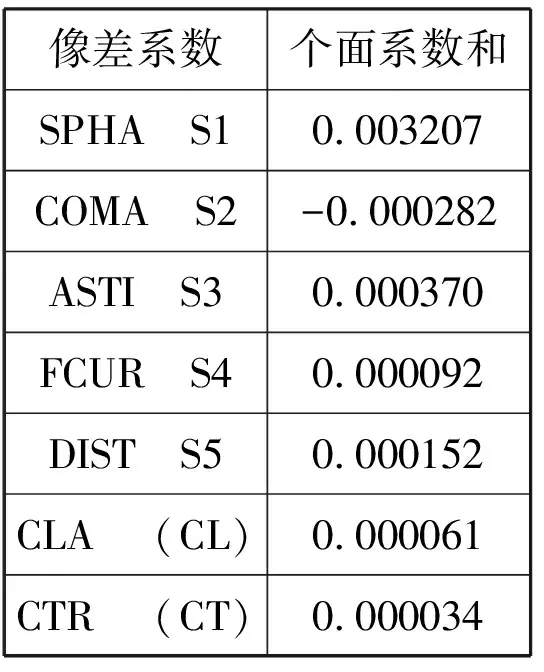
表1 赛德系数

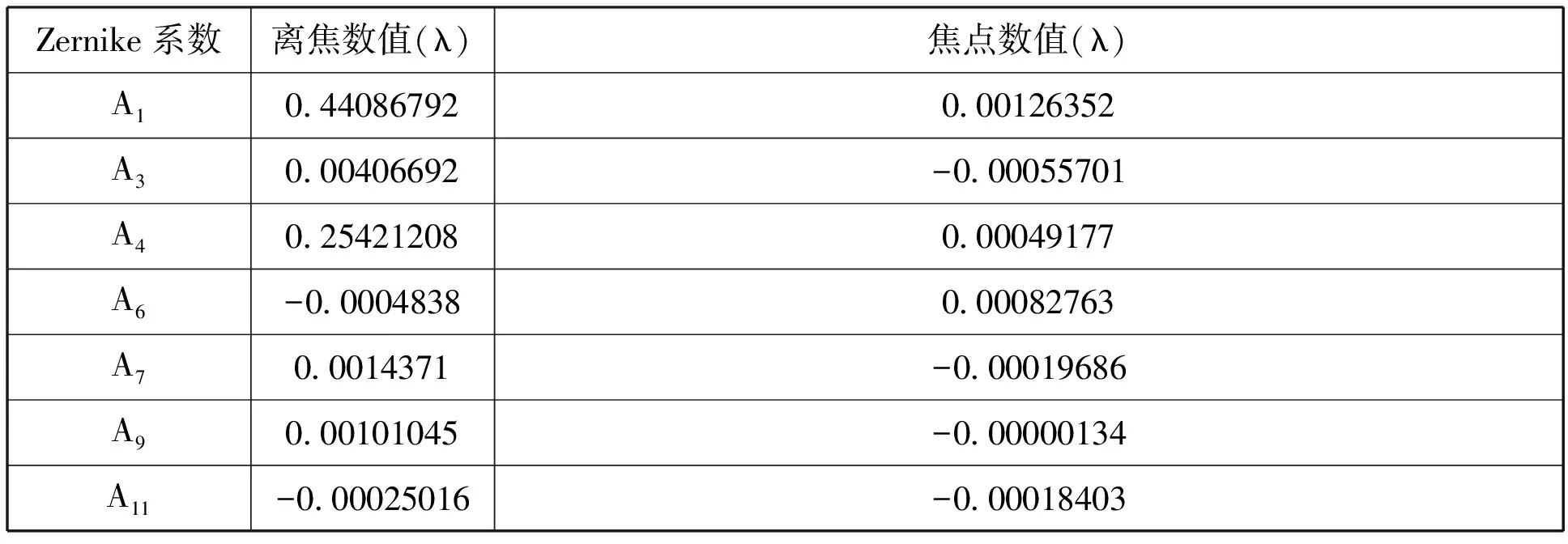
表2 泽尼克标准系数

由表1可以看出系统的像差系数值很小，一般都在千分位变化。这么小的像差系数对模拟的结果影响不大[2]，可以满足波前相位差法探测的要求，这一点在模拟结果中也可以证明。

此外，光学系统的像差还可以通过泽尼克系数来描述，同时还可以反应离焦量的情况。我们依然给出的是离焦像泽尼克的标准系数见表2。表2中给出了泽尼克标准系数的前11项，其中略去了数值为0的Z2、Z5、Z8、Z9、Z10项系数。A4为离焦，轴外数值对应的P-V值刚好为0.8806λ，这一数值刚好满足我们对离焦量的要求。A1为波前的整体涨落，可以不考虑，其它几项为像差，其数值较小，对结果的影响不大。

从表1、表2可以看出，根据晶体的偏振原理设计的波前相位差法探测器，获得的离焦量满足设计的要求，光学系统的像差不大。

3 模拟结果

假定望远镜的口径D=1m，焦距F=29.09m，大气视宁度r0=15cm，工作波长为550nm。在考虑波前相位差法探测所产生的像差，不考虑CCD产生的噪声影响下，做了下面的模拟实验。

原始图像和模拟的相位屏见图4和图5，由波前相位差法探测器的泽尼克系数和相位多样性算法可以得到模拟的焦面像和离焦图像[10]见图6和图7。根据相位多样性算法可以得到重建图像和重建相位见8和图9。

图4 原始图像

图5 模拟的相位屏

图6 模拟的焦面图像

图7 模拟的离焦图像

Fig.7 Simulated defocused image

图8 重建的图像

图9 重建的相位屏

由重建图像与原始图像对比可以看出图像的细节已经反应出来，重建的结果较为理想。重建相位与模拟相位的偏差值RMS≈0.0686λ ，由重建的结果可以看出我们设计的波前相位差法探测器是满足波前探测要求的，同样也表明文中波前相位差法探测器存在的像差对结果没有太多影响。

4 结 论

本文利用方解石的双折射特性，设计了一款新型的波前相位差法探测器。这款波前相位差法探测器具有光学系统简单，易于实现，两个图像的采集同步实时，并且获得的两个图像强度相当等诸多优点。由于利用了晶体偏振特性实现图像的分离，并获得合适的离焦量，不适合用于对偏振特性明显的目标进行探测。此外，这款波前相位差法探测器对不同的望远镜要进行具体的分析设计。文中给出了具体的设计参数，通过光学设计软件模拟，可以获得所需要的离焦量，并且其它像差不大，对波前探测没有大的影响。同时给出了波前相位差法探测器的像差系数和泽尼克系数，并根据离焦量、像差系数，做了数值模拟实验，模拟图像的重建结果较为理想。

[1] R A Gonsalves, R Chidlaw. Wavefront sensing by phase retrieval[J]. SPIE, 1979, 207:32-39.

[2] Ludovic Meynadier, Vincent Michau, Marie Therese. Noise propagation in wave-front sensing with phase diversity[J]. Applied Optics, 1999,38(23):4967-4979.

[3] R L Kendrick, Ray Bell, A L Duncan. Closed loop wave front correction using phase diversity[J]. SPIE,1998,3356:844-853.

[4] J M Simon, M C Simon.Wollaston prism as a beam splitter in convergent light[J]. Applied Optics,1978,17(21):3352-3353.

[5] Maria C Simon. Ray tracing formulas for monoaxial optical components[J]. Applied Optics, 1983,22(2):354-360.

[6] D S Acton, D Soltau, W Schmidt.Full-field wavefront measurements with phase diversity[J].Astronomy and Astrophysics, 1996, 309:661-672.

[7] A Blanc, T Fusco, M Hatrung, et al. Calibration of NAOS and CONICA static aberrations Application of the phase diversity technique[J]. Astronomy and Astrophysics, 2003, 399:373-383.

[8] 梁铨廷. 物理光学[M]. 北京：机械工业出版社，1979:199-203.

[9] Richard A Carreras, Greg Tarr, Sergio Restaino, et al. Concurrent computation of Zernike coefficients used in a Phase Diversity algorithm for optical correction[J]. SPIE, 1994, 2315:363-370.

[10] www.images.google.cn