行星际磁通量绳尺度的幂律谱分布

冯恒强,曹行健

(1.洛阳师范学院物理与电子信息学院, 洛阳 471022；2.同济大学,上海 210092)

行星际磁通量绳是太阳风中一种重要的磁结构。在早些时候，一般认为行星际磁通量绳有两类。一类是磁云，在行星际空间经常被探测到，它们具有大尺度的结构，直径约为0.2～0.4AU[1-4]。磁云是行星际日冕物质抛射(ICME)的一个重要子集，磁云同时具有以下3个基本特征: (1)磁场方向在大约一天的时间内发生大角度平滑旋转；(2)具有相对较强的磁场；(3)相对低的质子温度和等离子体β值[5]。由于磁云具有近似无力场位形，这种低β的封闭磁场结构使整个系统处于最小能量状态，能够长期维持下去，它可能保存了日冕内磁通量绳的信息，特别是各种冕环的磁结构信息，所以研究磁云对研究太阳活动的爆发环境、物理机制有重要意义。磁云和磁层作用时，其磁场的螺旋结构使它能够持续稳定地提供较强的南向磁场，从而和磁层顶的北向磁场发生重联，并导致较强的地磁暴。因此，磁云一直受到太阳物理学家和空间物理学家的广泛关注并对其做了大量的研究，取得许多重要的研究成果。如建立了能够基本描述磁云磁场位形的通量绳模型[4, 6-11]；磁云边界的认证以及磁云边界层新定义的确立[12-15]；多重磁云的观测、理论模型的建立及其对特大地磁暴的触发[16-18]；磁云在传播过程中膨胀演化的观测研究以及相应理论模型的建立[10, 19-20]；磁云和背景太阳风的相互作用以及在磁云边界层附近发生磁重联模型的提出[13-14]；磁云和地磁层的相互作用及其对地磁效应的触发机制等[21-24]。

Moldwin等在2000年发现行星际空间中还存在有另外一类小尺度磁通量绳结构，它们的持续时间仅有几十分钟，相应地空间尺度也只有～0.01AU，远低于一般磁云的尺度[25]。这些小尺度磁通量绳和磁云一样具有近似无力场的磁位形和较低的β值，但是小尺度磁通量绳不像磁云那样具有相对低的温度、密度和膨胀等观测特征。鉴于这些小事件和磁云都具有通量绳磁场位形而又存在很多不同特征，Moldwin等[25]对这些小事件的起源给出了两种可能解释。一种是小尺度磁通量绳也起源于日冕磁场重联，和磁云是同一类现象，只是尺度不同。另外一种是小尺度磁通量绳和磁云并不是同一类现象，磁云起源于太阳，小尺度磁通量绳起源于行星际空间，是日球电流片处磁场重联的结果。Moldwin等还指出，如果小尺度磁通量绳和磁云是同一类现象，其尺度分布应该是连续的，但是在这么多年的磁云研究中，从没有在地球附近观测到持续时间为几个小时的中等尺度磁通量绳事件的报道，所以他们认为小事件和磁云为同一种现象的可能性不大。

最近，我们通过完整、仔细地搜索Wind卫星从1995年到2001年的观测资料，证认出了144个行星际磁通量绳事件，进一步分析显示它们的尺度从小于0.01AU的小尺度磁通量绳到大于0.4AU的大尺度磁云呈现连续分布，而非小尺度与大尺度的“双峰”分布。通过估算这些行星际磁通量绳的能量还发现其能量也呈现连续分布。另外，我们还发现不同尺度(小、中、大)磁通量绳的物理性质随着尺度的增加发生缓慢变化，如中等尺度磁通量绳既有小通量绳的特性又有磁云的特性，而时间尺度每相差1～2小时的磁通量绳之间没有突变的特征。即很难从其磁场和等离子体特征上判断它们不是同一类现象。于是，我们认为所有磁通量绳都直接起源于太阳上的爆发[26]。

物理量的规律分布往往是由其内部的物理规律决定的，最常见的分布有高斯分布和幂律分布。对研究对象的分布规律进行研究是我们全面认识研究对象的一个重要手段。如Drake[27]在1971发现太阳耀斑爆发时软X射线的最大通量的分布呈现幂律分布，即耀斑的发生率随X射线的最大通量的变化可近似用幂律形式来表示；到1974年Datlowe等[28]发现耀斑爆发时硬X射线的最大通量也呈现类似的分布；1977年Lites和Hansen[29]发现太阳上存在小的远紫外(EUV)波段的脉冲爆发，Athay[30]认为这些小爆发是微耀斑。后来研究发现包括大耀斑至纳耀斑(比微耀斑更小)的所有耀斑的总能量都呈现幂律谱分布[31-33]。其实，这些幂律分布是它们属于同类爆发活动的外在反映，可以用统一的耀斑爆发理论解释。同样所有行星际磁通量绳的尺度呈现规律分布也是所有尺度的磁通量绳起源于太阳的一个重要证据。

本文是对我们前期工作[26]的延续工作，主要是对前面工作的补充， 即从行星际磁通量绳的数目随其尺度的变化形式来进一步论述中小尺度的行星际磁通量和太阳上的爆发活动的可能关系。

1 资料分析

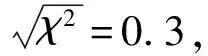
标准常α无力场轴对称模型用Lundquist解[11]描述:

(1)

其中B0为磁通量绳轴上的磁场强度，H=±1表示磁通量绳的螺旋性(+1为右手螺旋，-1为左手螺旋)，J0、J1分别为零阶、一阶贝塞尔函数，R为到磁通量绳轴的径向距离。运用最小二乘法拟合确定磁通量绳的直径通过以下步骤实现:(1)将观测磁场无量纲化;(2)用最小方差分析法(Minimun Variance Ananlysis，MVA)估计磁云的轴向，建立磁通量绳坐标系(即以磁通量绳的轴向为坐标系Z轴，取卫星轨道方向为S，则Z×S的方向为Y轴，最后X轴的方向可通过Y×Z得到。)并确定磁通量绳的螺旋性；(3)将无量纲化的观测磁场转换到磁通量绳坐标系，然后求无量纲化观测磁场和模型磁场的最小方差，通过多次迭代最后求得最小方差χ2从而确定轴的方向和卫星轨道离磁通量绳轴的距离(d0),其中

(2)

上式中N是所用磁场矢量的个数，这里在拟合时对数据进行了25份平均，即取N= 25。上标O和M分别代表观测磁场和模型磁场，下标C是指在磁通量绳坐标系。(4)运用拟合结果和磁通量绳速度的平均值，通过空间关系，可以得到磁通量绳的直径。关于最小二乘法拟合的详细描述可以参考文献[4]。

2 行星际磁通量绳的尺度谱

根据上述最小二乘法拟合可以估算出所有144个行星际磁通量绳的直径。拟合结果显示磁通量绳的直径分布在0.004 AU到0.6 AU之间，平均直径为0.14 AU，其中尺度最小的事件持续时间只有27min。为了分析行星际磁通量绳的发生率和其尺度的关系，将这144个事件按照拟合所得直径从小到大进行排序，每个事件的序号N(D)代表在1995年1月到2001年9月这段时间内所有尺度小于其直径D的磁通量绳数目。图1给出了事件的序号N(D)和直径的对照关系。由图1可以看出行星际磁通量绳的尺度分布是连续的，没有出现明显间断。有了事件的序号N(D)，则可以估算磁通量绳的发生率P(D)：

P(D)=ΔN/ΔD

(3)

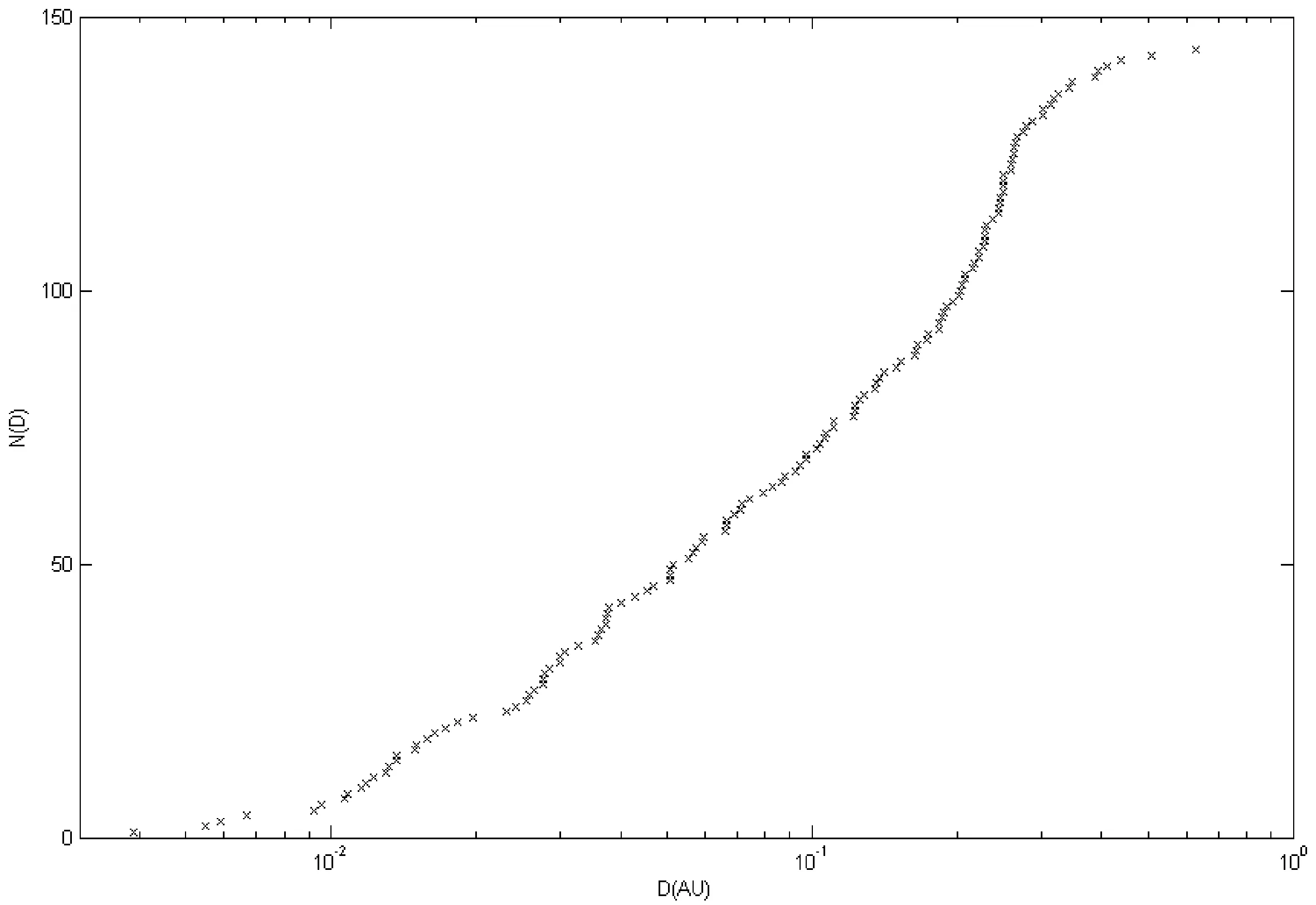
图1 横坐标是磁通量绳的直径，纵坐标是所有小于这个直径的通量绳数目Fig.1 The X-axis is for the diameters of interplanetary magnetic flux ropes,and the Y-axis is for the cumulative numbers of events with the diameters less than given values.

在利用公式(2)计算P(D)的时候我们取ΔN等于5。因为如果ΔN选取的较小，有些磁通量绳的尺度差别较小会造成P(D)很大，从统计学的角度上应该避免。磁通量绳的发生率随着其尺度的增加而较少，在这144个事件中值在0.0040～0.3000AU之间的就有133个。如果取ΔN等于5,那么平均的ΔD等于0.0098AU，而最小的ΔD为0.0053AU。也就是说对于直径在0.0040～0.3000AU之间的磁通量绳，平均的ΔD差不多是最小的ΔD的2倍，所以选取ΔN等于5不会造成P(D)过大影响计算结果。至于直径分布在0.03～0.6AU之间的磁通量绳，ΔD更大，更不会影响P(D)的计算结果。图2给出了磁通量绳的发生率P(D)和直径D的对照图。由图2可以看出P(D)随着直径D的增加几乎呈幂律下降，拟合结果显示：

P(D)≈64D-0.768

(4)

拟合的相关性系数为0.79。我们的前期工作曾经给出行星际磁通量绳的发生率和能量的关系也呈现幂律分布，其幂指数为-0.869[26]。两者十分相似，其实两者是紧密相关的。通常来说，尺度越大磁通量绳包含物质就越多，磁场也越强，总的能量也就越大。但是尺度和能量不是绝对的线性关系，所以磁通量的发生率随两者的变化趋势相似。

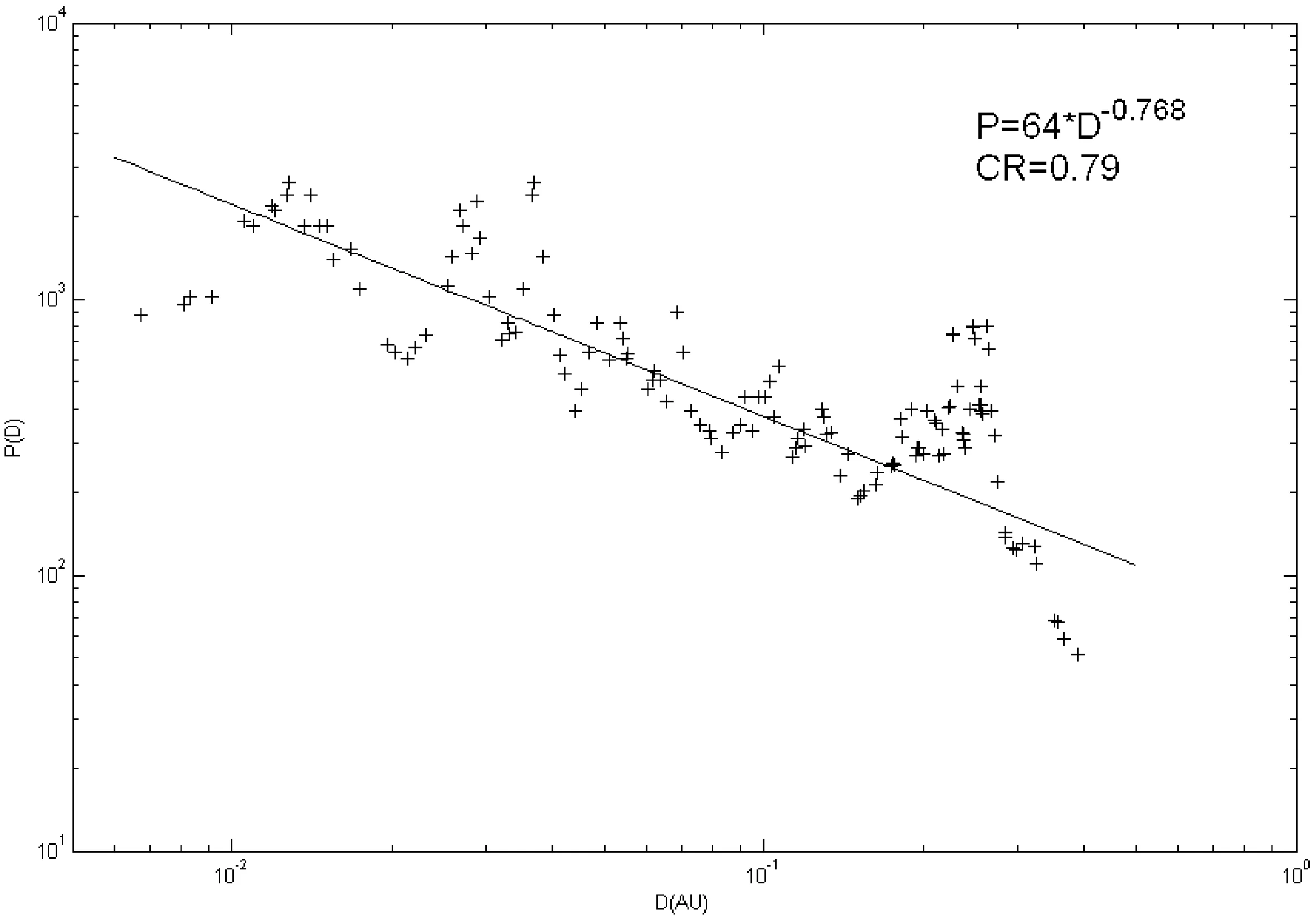
图2 磁通量绳的发生率P随直径D的变化图Fig.2 The occurrence rate (P) of interplanetary magnetic flux ropes as a function of diameter (D)

由图2还可以看出在0.18～0.3AU之间，计算所得的P(D)有一个明显的凸起。这个凸起可能由以下两方面原因引起。一是大于0.15AU的磁通量绳事件持续时间比较长(通常大于10小时)，在分析卫星资料的时候不容易被错过；而较小尺度的磁通量绳容易受背景太阳风扰动的影响而错过。另外，较大尺度的磁通量绳相对于较小尺度的也比较容易被卫星观测到，因为尺度越大“碰撞界面”就越大。所以如果排除上面两方面原因的影响，磁通量绳的发生率随尺度的变化可能会呈现更好的幂律分布。

3 行星际磁通量绳和太阳活动的可能关系的讨论

在前面提到各种尺度的耀斑的发生率相对于总能量呈现幂律谱分布是由它们服从的耀斑爆发理论所决定的。同样我们相信行星际磁通量绳的发生率相对其直径呈现幂律谱分布也是由共同的爆发理论(条件)所决定的，即所有尺度的行星际磁通量绳都直接起源于太阳上的爆发，而和磁云对应于通常的日冕物质抛射(CME)一样，较小尺度的通量绳对应相对较小的CME(如：micro-CME、nano-CME)。而较小CME的强度太弱，受目前观测技术的限制而没有被日冕仪观测到。耀斑和CME都是太阳大气中常见的爆发活动，耀斑和CME所释放的能量相当，所以从第一个CME事件观测到以后，人们就试图把两者联系起来，寻找它们之间的相互关系。30多年来，不少研究学者在这方面做了大量工作，但是有的学者认为耀斑和CME关系密切，是耀斑触发了CME的产生[34-35]；有的认为是CME触发了耀斑的产生[36]；最近Lin等建立了CME和太阳耀斑爆发的Lin-Forbes模型，提出耀斑和CME是太阳大气中同一种爆发的不同部分或不同阶段[37-38]。如果Lin等对耀斑和CME关系的解释是正确的，大的耀斑就会和大的CME相关，微耀斑就会和我们猜测的对应中下尺度的行星际磁通量绳的小CME相关。进一步可以推出行星际磁通量绳尺度的幂律谱分布和耀斑总能量的幂律谱分布可能是有关系的。因为太阳耀斑的能量和尺度总体上是正相关的(不一定是线性)，即大尺度耀斑具有较高的能量，所以太阳耀斑的能量分布在一定程度上反映了其尺度的分布。按照一般推断，CME爆发的尺度也会与其相关的耀斑爆发能量成正相关，CME的尺度分布也可能呈现幂律谱分布，以至于CME的行星际对应物(行星际磁通量绳)的尺度呈幂律谱分布。当然，上面对行星际通量绳、CME和耀斑关系的讨论只是一种推测，由于耀斑和CME都没有规则的形状，用不同波段的光去观测耀斑和CME呈现的形状也不一样，所以对其做尺度分布的研究很困难。

致谢：感谢NASA/GSFC提供Wind卫星的关键数据。

[1] Marubashi K. Structure of the interplanetary magnetic clouds and their solar origins [J]. Adv Spa Res, 1986, 6: 335-338.

[2] Burlaga L F. Magnetic clouds and force-free fields with constant alpha [J]. J Geophys Res, 1988, 93: 7217-7224.

[3] Richardson I G, Cane H V. The fraction of interplanetary coronal mass ejections that are magnetic clouds: Evidence for a solar cycle variation [J]. Geophys Res Lett, 2004, 31: L18804.

[4] Lepping R P, Burlaga L F, Jones J A. Magnetic field structure of interplanetary magnetic clouds at 1 AU[J]. J Geophys Res, 1990, 95: 11957-11965.

[5] Burlaga L F, Sittler E, Mariani F, et al. Magnetic loop behind an interplanetary shock: Voyager, Helios, and IMP 8 observations [J]. J Geophys Res, 1981, 86: 6673-6684.

[6] Vandas M, Romashets E P, Watari S. Potential magnetic fields around flux ropes [J]. Astron Astrophys, 2003, 412: 281-292.

[7] Vandas M, Romashets E, Watari S. Magnetic clouds of oblate shapes [J]. Planetary and Space Science, 2005, 53: 19-24.

[8] Hidalgo M A, Cid C, Medina J, et al. A new model for the topology of magnetic clouds in the solar wind [J]. Sol Phys, 2000, 194: 165-174.

[9] Hidalgo M A, Cid C, Vinas A F, et al. A non-force-free approach to the topology of magnetic clouds in the solar wind [J]. J Geophys Res, 2002, 107(A1): 1002.

[10] Hidalgo M A. A study of the expansion and distortion of the cross section of magnetic clouds in the interplanetary medium [J]. J Geophys Res, 2003, 108: 1320.

[11] Shimazu H, Vandas M.A self-similar solution of expanding cylindrical flux ropes for any polytropic index value [J]. Earth Planet space, 2002, 54: 783-790.

[12] Feng H Q, Wu D J, Chao J K. Identification of configuration and boundaries of interplanetary magnetic clouds [J]. J Geophys Res, 2006, 111: A07S90.

[13] Wei F S, Liu R, Fan Q, et al. Identification of the magnetic cloud boundary layers [J]. J Geophys Res, 2003, 108(A6): 1263.

[14] Wei F, Liu R, Feng X, et al. Magnetic structures inside boundary layers of magnetic clouds [J]. Geophys Res Lett, 2003,30(24): 2283.

[15] 魏奉思, 刘睿, 范全林, 等. 行星际磁云边界层特征及边界新定义[J]. 中国科学(E), 2002, 32(5): 608-617.

[16] Wang Y M, Wang S, Ye P Z. Multiple magnetic clouds in interplanetary space [J]. Sol Phys, 2002, 211: 333-344.

[17] Wang Y M, Ye P Z, Wang S. Multiple magnetic clouds: Several examples during March-April 2001 [J]. J Geophys Res, 2003, 108(A10): 1370.

[18] Wang Y, Zheng H, Wang S, et al. MHD simulation of the formation and propagation of multiple magnetic clouds in the heliosphere [J]. Astron Astrophys, 2005, 434: 309-316.

[19] Farrugia C J, Burlaga L F, Osherovich V A, et al. A study of an expanding interplanetary magnetic cloud and its interaction with the earth’s magnetosphere:the interplanetary aspect [J]. J Geophys Res, 1993, 98: 7621-7632.

[20] Farrugia C J, Osherovich V A, Burlaga L F. Magnetic flux rope versus the spheromak as models for interplanetary magnetic clouds [J]. J Geophys Res, 1995, 100: 12293-12306.

[21] Wu D J, Chao J K, Lepping R P. Interaction between an interplanetary magnetic cloud and the Earth’s magnetosphere:Motions of the bow shock [J].J Geophys Res,2000,105:12627-12638.

[22] Wang Y M, Ye P Z, Wang S, et al. An interplanetary cause of large geomagnetic storms: Fast forward shock overtaking preceding magnetic cloud [J]. Geophys Res Lett, 2003, 30(13): 1700.

[23] Wu C C, Lepping R P. Effects of magnetic clouds on the occurrence of geomagnetic storms: The first 4 years of Wind [J]. J Geophys Res, 2002, 107(A10): 1314.

[24] Wu C C, Lepping R P. Effect of solar wind velocity on magnetic cloud-associated magnetic storm intensity [J]. J Geophys Res, 2002, 107(A11): 1346.

[25] Moldwin M B, Ford S, Lepping R, et al. Small-scale magnetic flux ropes in the solar wind [J]. Geophys Res Lett, 2000, 27: 57-60.

[26] Feng H Q, Wu D J, Chao J K. Size and energy distributions of interplanetary magnetic flux ropes[J]. J Geophys Res, 2007, 112: A02102.

[27] Drake J F. Characteristics of Soft Solar X-Ray Bursts[J]. Sol Phys, 1971, 16: 152-185.

[28] Datlowe D W,Elcan M J,Hudson H S.OSO-7 observations of solar X-rays in the energy range 10-100 keV [J]. Sol Phys, 1974, 39: 155-174.

[29] Lites B W, Hansen E R.Ultraviolet brightenings in active regions as observed from OSO-8 [J]. Sol Phys, 1977, 55: 347-358.

[30] Athay R G. Are EUV bursts members of the flare family? [J]. Sol Phys, 1984, 93: 123-131.

[31] Parker E N. Nanoflares and the solar X-ray corona [J]. Astrophys J, 1988, 330: 474-479.

[32] Hudson H S. Solar flares, microflares, nanoflares, and coronal heating [J]. Sol Phys, 1991, 133: 357-369.

[33] Craig I J D. A reconnection model for the distribution of flare energy [J]. Sol Phys, 2001, 202: 109-115.

[34] Wu S T,Dryer M,Han S M.Non-planar MHD model for solar flaregenerated disturbances in the heliospheric equatorial plane [J], Sol Phys, 1983, 84: 35-418.

[35] Maxwell A, Dryer M, McIntosh P. A piston-driven shock in the solar corona[J], Sol Phys, 1985, 97: 401-413.

[36] Kahler S W. Solar flares and coronal mass ejections [J]. Ann Rev Astr Ap, 1992, 30: 113-141.

[37] Lin J, Forbes T G. Effects of reconnection on the coronal mass ejection process [J]. J Geophys Res, 2000, 105: 2375-2392.

[38] Lin J, Raymond J C, Van Ballegooijen A A. the role of magnetic reconnection in the observable feature of solar eruptions [J]. Astrophys J, 2004, 602: 422-435.