Sn上的变换群探究

邓艳娟，陈 军

(中国青年政治学院 经济系,北京 100089)

1 Sn上的简单介绍

Sn为n维球空间，定义为

1.1 球坐标表示

下面讨论中，用·代表欧氏内积，<,>代表洛伦兹内积.令C为Sn上的中心为c∈Sn，弧度为θ，0<θ<π的n维闭-cap，

C={x∈Sn∶x·c≥cosθ}.

(1)

此时对于Sn上的属于C的点x我们可以表示为

x·c-1·cosθ≥0,

(2)

由于sinθ>0,我们有

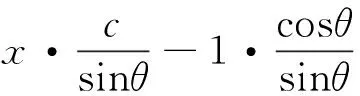
(3)

可用(n+2)维向量来表示点x和cap-C,令

(4)

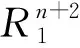
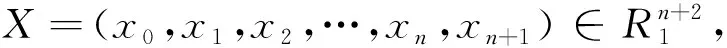
即确定了Sn上的一个定向球.由上可知，

定理1 球空间上的定向球与洛伦兹空间中的点一一对应.

≥0.

(5)

性质1 (1)如果一个向量C表示一个cap当且仅当C满足条件=1；(2)如果一个向量表示一点X当且仅当=0并且X的第一个分量为1.

由此规定，如果有正数λ，点λX与X表示同一点.

如果一个capC=(cotθ,cscθc)的中心为c，弧度为θ，那它的补C′记为中心为-c，弧度为π-θ的cap.C′的坐标表示记为-C.

性质2 n-1维球上的点X是C和C′的公共边界点当且仅当=0.

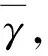
特别的，当γ是大圆时，反演就是得到γ的那个截Sn的平面的反射.如果γ不是大圆，那么就有Rn+1中唯一一点与γ上点的连线与Sn相切.

由于球坐标的引入，可将球上的反演线性化.所以有

定理2U关于C和C′的公共边界的反演记为线性变换

U→U′=U-2C

(6)

证明 只需验证变换保持线性和保内积.

假设U,V为球上cap，U′,V′为U,V关于C和C′的公共边界的反演，所以有内积

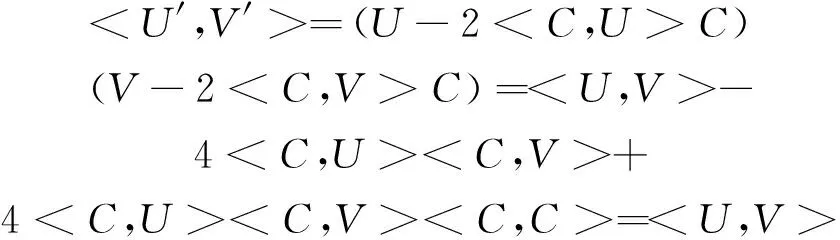
(7)

对于球上的点上式同样成立.由此说明变换将cap映成cap，点映成点.特别的，当C为半球时，即C=(0,c)(C的第一个分量为0)，c为n-维平面的法向，此时反射即为我们的反演.点X=(1,x)的反射

x→x-2(c·x)c.

通常情况下，C不是半球时，点X的反演可写成

(8)

其中

λ=⎣1+cos2θ-2(c·x)cosθ」csc2θ

(9)

容易看出λ>0并且==0，X′是球上的点，并且可看出点x′是x和θc的线性组合.

1.2 定向球之间的位置关系

任意两个定向球C1=(cotθ1,cscθ1c1),C2=(cotθ2,cscθ2c2).=cosθ,其中θ为两个定向球之间的夹角.

由洛伦兹内积我们有，

(10)

另一方面，x∈定向球C上，有法向量n在C和x确定的平面上，C=ax+bn,a=C·x=cosθ.同时又有=1，故可得到b=sinθ.因此，

(11)

由此可看出

定理3 两个定向球之间的夹角即为两个定向球法向之间的夹角.

通过夹角θ，可以来判断两个定向球的位置关系：

(1)当θ=0，两个定向球相内切，=1；

(2)当θ=0，两个定向球相外切，=-1；

(3)当θ≠0,π，两个定向球相交，||<1；

(4)两个定向球相外离，即||>1;

(5)两个定向球正交，即=0.

1.3 相切的定向球之间的位置关系

定理4 定向球C1,C2∈Sn，C1,C2相切，即

===1，则有

tC1+(1-t)C2,t∈R.

证明 过C1,C2的直线为

C=tC1+(1-t)C2∈Sn,t∈R,

(12)

此时说明Sn上相切的一簇定向球对应洛伦兹空间中的一条直线.

2 Sn上的四种变换群

定义1 球Sn上反演变换的复合就是Möbius变换群.

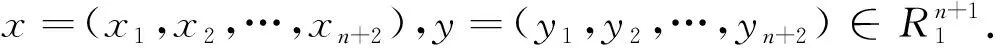
性质3 保正向的洛伦兹变换群O+(n+1,1)是O(n+1,1)的子群.

定义3 如果映射σ∶Sn→Sn是微分同胚且满足σ*g=λg,λ∈C∞，这时我们称σ为Sn上共形变换群.

定义4 如果映射σ∶Sn→Sn是微分同胚且把Sn上每个Sn-1变成Sn-1，这时我们称σ为Sn上保球换群.

性质4 保球变换将定向球映到定向球.

参考文献：

[1] Blaschke. W.Verlesungen ueber Differentiallgeometry.Vol[M]. Springer, Berlin , 1929.

[2] Bryant, R.A dualitytheorem for Willmore surfaces[J].Differential Geom, 1984(20):23-53.

[3] J. B. Wilker.Inversive geometry[M].The geometric vein (C. Davis, et ah, eds.), Springer, New York, 1981.

[4]Kulkarni, R.S. and Pinkall, U. Conformal Geometry.Aspecs[M].Math. E12, Friedr. Vieweg Son, Braunschweig, 1988.

[5]Li, H.Zh., Liu, H.L., Wang, C.P. and Zhao, G.S., M bius isoparametric hypersurfaces inSn+1with two distinct principle curvatures[J]. Acta Math. Sinica, English series , 2002(18):437-446.