桩土界面荷载传递模型的改进及其数值实现

蒲诃夫， 郑俊杰， 章荣军

(华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

桩土相互作用问题是岩土工程领域的一个十分重要的问题，桩土界面的荷载传递模型对于预测桩的承载变形性状有着重要的影响。合理准确的荷载传递模型是分析桩的承载力、沉降及变形等方面问题的关键所在。20世纪50年代Seed和Reese[1]等人提出了基于荷载传递法的双曲线模型来分析桩土界面荷载传递，取得了很好的计算结果；后来，Kezdi[2]提出了以指数函数作为荷载传递模型的方法，对刚性桩进行了分析； Vijayvergiya[3]提出了抛物线形式的荷载传递函数，考虑了桩周土体在受荷过程中的非线性；辛公锋[4]等人对双曲线模型进行修正和扩充，提出了既能考虑侧阻软化又能考虑侧阻硬化的广义双曲线模型；陈龙珠[5]采用双折线硬化模型，分析了桩周和桩端土特性参数对荷载-沉降曲线的影响。陈明中[6]用三折线模型作为传递函数，分析了土体强度随深度增加的特性，推导出了单桩的荷载-沉降关系的近似解析解。张忠苗课题组[7]提出了可考虑桩土软化的桩侧传递函数的统一三折线模型。

上述这些荷载传递模型在桩土相互作用分析方面都具有较好的适用性和准确性，但目前常见的数值分析软件为了分析的方便都没有采用这些形式的荷载传递模型，而是采用了更加简便的理想弹塑性模型，这样的处理方法虽然使得软件的使用者操作起来更加简单，但却牺牲了模拟的精度，降低了模拟结果的可信度。以有限差分软件FLAC3D为例，FLAC3D采用的是理想弹塑性模型来模拟桩土界面的相互作用问题，这样的处理有三个明显的缺陷：第一，桩土界面耦合弹簧的刚度值没有一个合理的确定依据，软件使用者一般都是首先采用一个估计值，然后根据计算结果的准确度再不断地调整，这样的方法具有很大的主观性和随意性，计算出的结果往往不可靠；再者，荷载工作范围不同就应该选取不同的初始值，这样才能在应用理想弹塑性模型来表达桩土界面特性时取得较好的计算结果。对于已知荷载工作范围的模拟而言，通过选取适当的k值虽然也能够取得较好的计算结果，但对于不知道荷载工作范围的情况而言，k值的确定就只能靠经验来猜测了。第二，耦合弹簧的刚度值k在给定之后就一直不变了，而事实上，桩土界面的应力-应变关系是非线性的，因此理想弹塑性模型不能真实地反映桩土界面的相互作用特性。第三，耦合弹簧的刚度值k的确定一般都忽略了深度效应的影响。

为克服上述缺陷，本文基于有限差分软件FLAC3D，利用FLAC3D软件内嵌的FISH语言进行桩土界面荷载传递模型的二次开发，采用双曲线模型代替FLAC3D软件内嵌的理想弹塑性模型，并将Alonso[8]所提出的确定桩土界面的初始剪切刚度的方法应用到FLAC3D中，将两种模型下所计算出的结果与文献[9]中的结果进行对比分析。

1 传统荷载传递模型

自Seed和Reese等人提出软黏土中桩身荷载传递的双曲线模型以来，许多学者在荷载传递模型方面进行了研究，对双曲线荷载传递函数做出了各种不同的简化和改进或提出新的传递函数模型，应用最广的有以下几种模型。

1.1 双曲线模型

Wong和Teh等[10]假定桩土界面上的剪应力τ与桩土相对位移Δ呈双曲线关系，如图1(a)所示，其表达式为：

(1)

式中,τ，Δ分别为桩土界面上的剪应力和桩土相对位移；ksi和τult分别为桩土界面的初始剪切刚度和极限剪应力。Poulos和Davis[11]根据Coulomb定律，指出τult可由下式确定：

τult=c+σm×tanφ

(2)

式中，c为桩土界面黏结强度，σm为有效约束应力，φ为桩土之间的摩擦角。

1.2 修正双曲线模型

罗斌[12]、辛公锋[4]等人在现场试验、室内常规试验与离心模型试验的基础上对上述双曲线模型进行修正和扩充，分别提出了能够考虑侧阻软化的修正双曲线模型和既能考虑侧阻软化又能考虑侧阻硬化的广义双曲线模型，其函数表达式分别为式(3)和式(4)：

(3)

(4)

式中，a,b,c均为双曲线模型参数。考虑侧阻软化的双曲线模型适用于深厚软土中的大直径超长桩；而考虑侧阻硬化的双曲线模型适用于加工硬化型土中的桩土相互作用分析。

1.3 统一三折线模型

张忠苗课题组[7]在总结前人研究成果的基础上提出了可考虑桩周土软化和硬化的桩侧传递函数统一三折线模型，如图1(b, c, d)所示。桩侧土的荷载传递函数可统一表达为：

(5)

式中，τs为桩侧摩阻力(Pa)；s为桩身相邻的土结点位移(m)；λ1，λ2为桩侧土弹性阶段和塑性阶段(硬化或软化)的剪切刚度系数(Pa/m)；su1为弹性阶段和塑性阶段的界限位移(m)；su2为塑性阶段和滑移阶段的界限位移(m)；β为强度系数。

上述模型中，λ2>0,λ3≥0且β>1时表示侧阻硬化(如图1(b)所示)；λ2<0,λ3=0且0<β<1时表示侧阻软化(如图1(c)所示)；当λ1>0,λ2=λ3=0且β=1时，su2=su1，此时表示的是理想弹塑性模型(如图1(d)所示)。该三折线模型可统一表示桩侧土的三种计算模型。

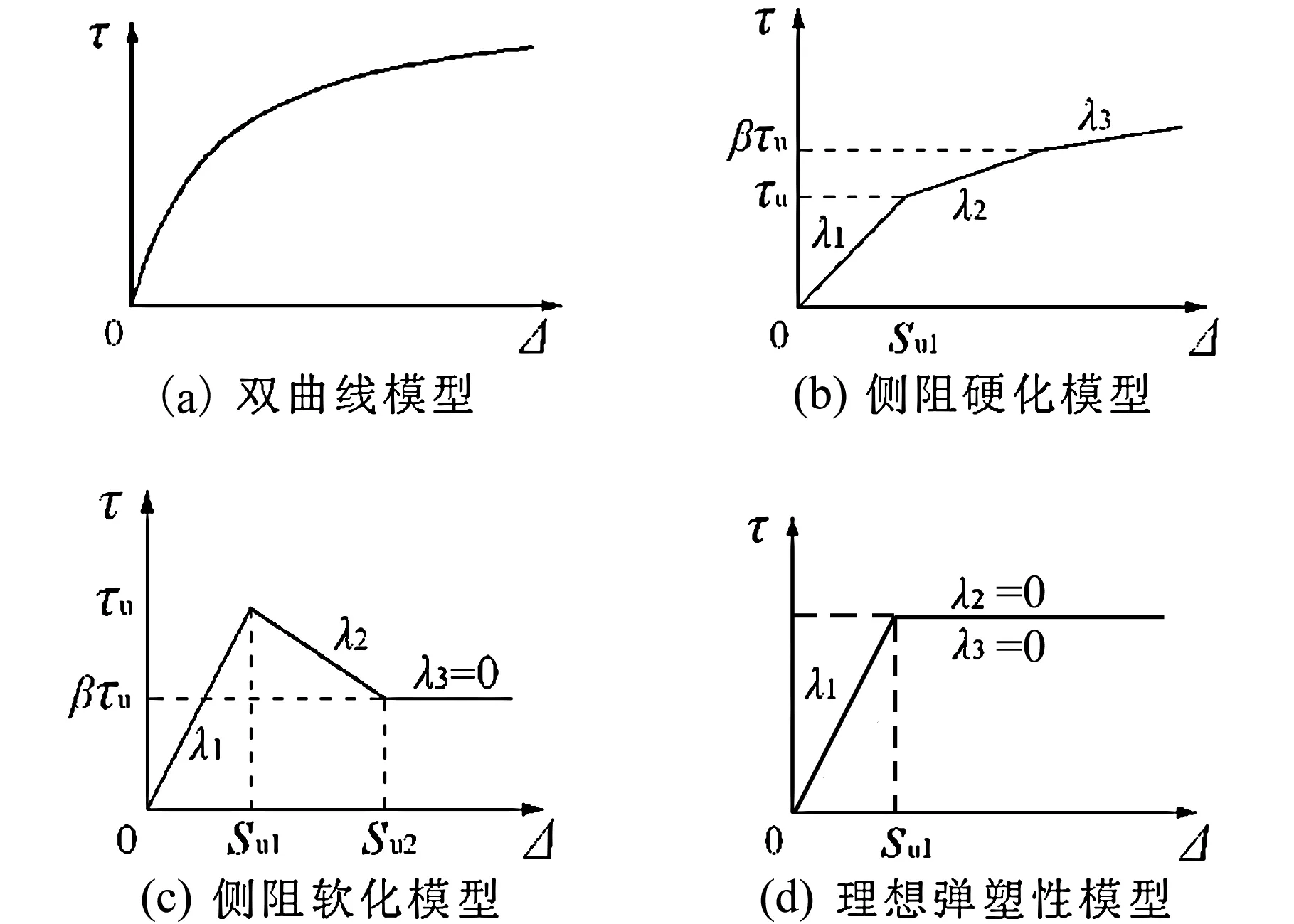
图1 传统荷载传递模型

2 FLAC3D中桩土界面模型

FLAC3D中桩土相互作用的实现过程与荷载传递法很相似，即在FLAC3D中，桩单元与土的相互作用是通过剪切和法向的耦合弹簧实现的。这些耦合弹簧是非线性结点，它使得桩单元结点与土体之间进行了力和运动的传递，法向耦合弹簧用来模拟桩土界面法向上的相互作用，如桩周土对桩的挤压效果等，且能考虑桩土之间的分离状况；切向耦合弹簧用来模拟桩土接触面的切向上的相互作用，这些非线性弹簧的应力-应变关系即表示桩侧摩阻力τ(或桩端抗力σ)与剪切位移Δ之间的关系。

2.1 法向耦合弹簧的力学特性

桩和网格接触面的法向特性就是自然的粘结特性和摩擦作用，其力学特性由法向耦合弹簧刚度kn、粘结强度cn、摩擦角φn、外圈周长P、裂缝标志及有效约束应力σm共同决定(图2)。

图2 法向耦合弹簧力学特性

2.2 剪切耦合弹簧的力学特性

桩和网格接触面的剪切特性与法向特性类似，也是自然的粘结特性和摩擦作用，其力学特性由剪切刚度ks、粘结强度cs、摩擦角φs、外圈周长P及有效约束应力σm共同决定(图3)。

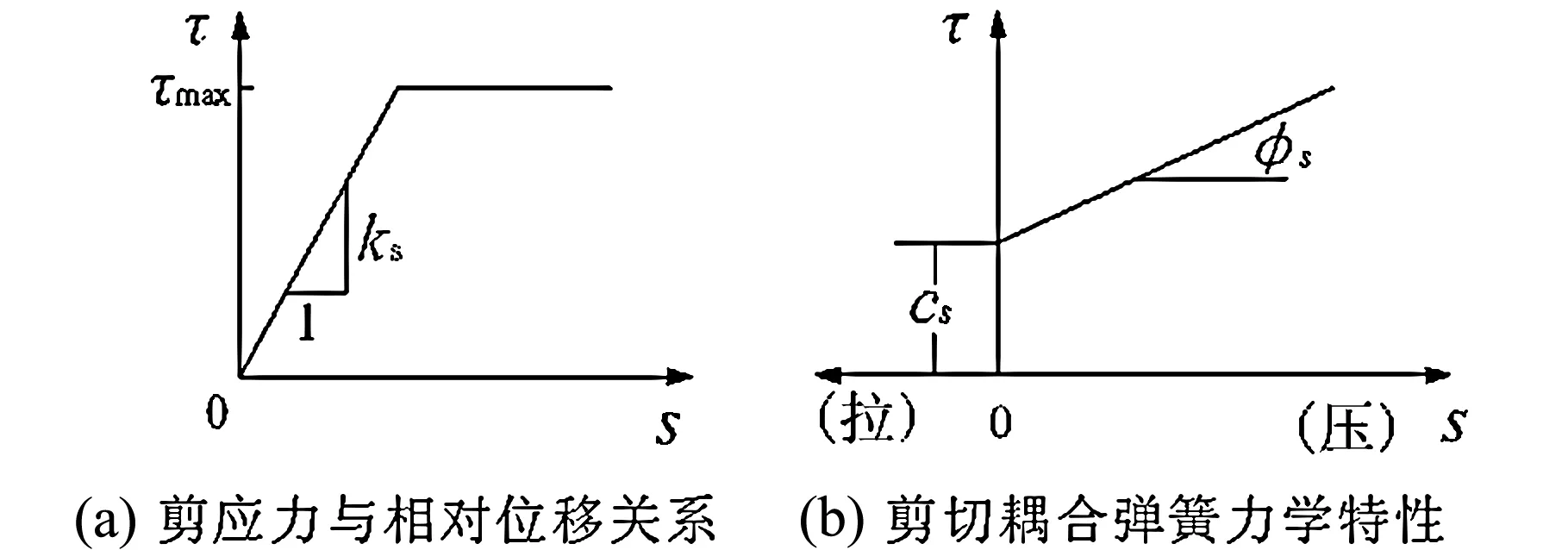
图3 剪切耦合弹簧力学特性

这一处理方法其实就是类似于荷载传递法中的理想弹塑性模型，只是荷载传递法中没有考虑桩土的分离，而FLAC3D中考虑了桩土的分离。在该模型中，当桩土相对位移较小时，剪应力与相对位移成线性关系，即剪切刚度ks保持不变，剪应力随相对位移增加而线性增加；当桩土相对位移增加到极限相对位移Δcr以后，剪应力为恒定值，等于界面的剪切强度，此后不再随桩土相对位移的增加而增加。

这样的处理方式比较简单，在数值模拟中需要输入的参数较少，应用起来比较方便，但缺点是忽略了桩土界面的非线性特性，从而导致模拟精度降低。Desai[13], Uesugi[14], Yin[15]等人所做的SSI(Soil Structure Interface)试验及大量的工程测量数据[7]表明，双曲线模型能够更好地反映桩土界面剪切性状的非线性特性，基于这一考虑，本文利用FLAC3D内嵌的FISH汇编语言通过自编的程序用双曲线模型代替FLAC3D内嵌的理想弹塑性模型，对比分析两种情况下桩土相互作用的不同结果。

3 改进桩土界面模型及数值实现

3.1 改进桩土界面模型

对于如何确定FLAC3D中桩土界面初始刚度值的问题，目前还没有一个合理的取值依据和方法。Wong和Teh等人[10]建议采用Randolph和Wroth[16]提出的经验公式ksi=2πGiL/ln(rm/r0)，式中Gi为第i层土的土体剪切模量，L为桩长，r0为桩半径，rm为桩的影响半径，rm=2.5Lρ(1-υs)，ρ为桩中点处的土体剪切模量与桩端底处的土体剪切模量的比值，υs为土体泊松比。这为桩土界面刚度值的确定方法提供了一定的参考，但这其中存在一个明显的理论缺陷，即该方法是基于剪切位移法提出的，剪切位移法中桩土位移是协调的，不考虑桩土之间的滑动，而FLAC3D中是考虑了桩土滑动的，因此直接用该方法并不妥当。

在荷载传递法中，桩土位移也是协调的，没有考虑桩在土中的滑动；而FLAC3D中考虑了桩土之间的相对滑动。因此从理论上讲，不能将荷载传递法中的双曲线模型直接应用到FLAC3D中。为了解决两者之间的不兼容问题，可采用Alonso[8]提出的方法来确定FLAC3D中的桩土界面初始刚度，即按照极限剪应力和极限相对位移的比值来确定，它能考虑桩土之间的滑移，且如此处理后就可将双曲线模型直接应用到FLAC3D中去了。

如图4所示，取桩土界面的τ～Δ双曲线的初始切线与τ=τult线的交点对应的桩土相对位移为表观极限相对位移Δau，即Δau=τult/ks。当取破坏比Rf=1.0时，Δau=τf/ks，为了将Δau与Δu建立联系，引入一个参数χ=Δu/Δau，通过调节χ使双曲线模型在桩土相对位移等于Δu时的剪应力τ(Δu)尽量接近极限剪应力τult。这样一来，桩土界面的初始剪切刚度ks与极限剪应力之间的关系就建立起来了，极限剪应力越大，ks越大。陈仁朋等[17]建议，为了避免ks过大，一般取χ=4可满足要求。

该方法还能够考虑土的深度效应对ks和kn的影响。一般而言，土体越深处约束应力σm越大，桩土界面的极限剪应力τult越大，故而耦合弹簧刚度值也越大。此外，该方法也能考虑到桩侧土的土类和土性的影响。根据工程经验，对于黏性土，发挥极限侧阻所需位移约为6～12 mm，对于砂类土约为8～15 mm[7]。

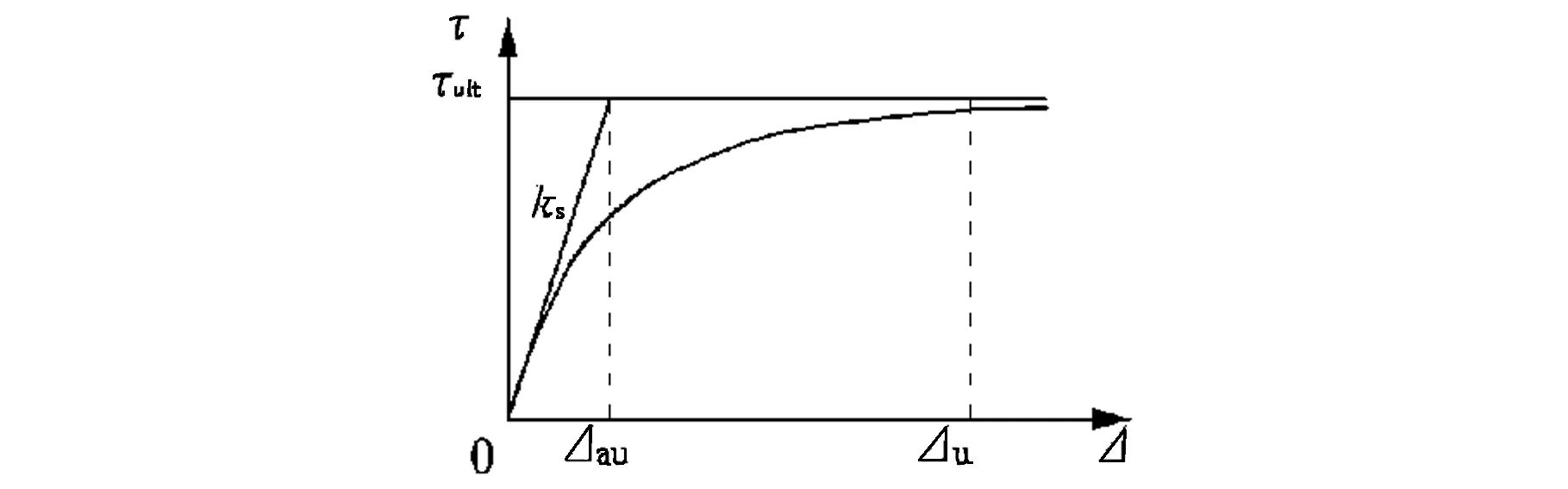
图4 桩土界面剪应力与相对位移的关系曲线

3.2 改进桩土界面模型的实现过程

在FLAC3D内嵌的理想弹塑性模型中，桩土界面耦合弹簧的刚度是一个不变的定值，在计算之前输入软件即可。而在双曲线模型或侧阻软化硬化模型等非线性模型中，耦合弹簧的刚度与桩土相对位移相关，当桩在荷载作用下逐渐产生位移时，桩土相对位移不断变化，耦合弹簧的刚度也就跟着不断地变化。且由于土体的深度效应，耦合弹簧的刚度应当是从上到下逐渐增大的。由于FLAC3D是基于增量法求解的软件，因此应当采用对这些非线性函数求导的方法来计算随桩土相对位移不断变化的耦合弹簧的刚度。

式(1)为剪应力τ与桩土相对位移Δ之间的关系，在该双曲线上任何一点的切线的斜率就是此状态下耦合弹簧的刚度，对式(1)求导可得：

(6)

ks,j即表示在桩土相对位移为Δj时所对应的耦合弹簧刚度；Δj为第j个耦合弹簧的变形(即桩单元第j个节点处桩土相对位移)；kini,j为第j个耦合弹簧的初始刚度；τult,j为第j个耦合弹簧的极限剪应力，由式(2)确定。

在FLAC3D的FISH语言中，用sp_rconf函数可提取出每个桩节点处的有效约束应力σm，将σm代入式(2)即可确定出τult,j；用sp_rdisp函数可提取即时的桩土相对位移Δj。将kini,j,Δj和τult,j一起代入式(6)即可确定出与桩土相对位移所对应的耦合弹簧刚度ks,j，最后，通过sp_cssk函数把ks,j的值赋予第j个耦合剪切弹簧。每进行20个计算步就计算一次最新的ks,j并将其值赋给弹簧刚度，这样一来即完成了用双曲线模型代替理想弹塑性模型的过程。事实上，对于任何非线性或线性的桩土界面模型，只要能给出相应的模型的函数，都可用该方法将其应用到桩土共同作用的分析中。

值得注意的是，为避免耦合弹簧由于突然受力而发生剧烈震荡，建议在桩土分析中采用在桩顶处施加均匀的速度的方法来施加荷载，如果要直接施加力的话，最好能够分很多步逐渐地加载。还有就是通过sel set damp combined语句为模型设置结合式阻尼，以进一步减小耦合弹簧的震荡。

4 实例验证

为了验证用FLAC3D进行桩土分析时双曲线模型比理想弹塑性模型具有更好的模拟效果，本文引用了Guo和Randolph[9]所做的一个桩土分析的例子，并分别采用FLAC3D内嵌的理想弹塑性形式的界面荷载传递函数和双曲线形式的界面荷载传递函数对其进行模拟，然后将模拟结果与Guo和Randolph所做的结果进行对比。

在该例中，一根长30 m，直径0.75 m的桩位于50 m厚的匀质土中。土体杨氏模量为E=1056 MPa，泊松比υ=0.49；桩体的杨氏模量为E=30 GPa，桩顶受一竖向荷载。在本例的FLAC3D所建模型(见图5)中，模型为100 m长，100 m宽，50 m高，共10000个单元体，11466个节点；顶面为自由面，在x=50 m和x=-50 m的面只约束x方向位移；在y=50 m和y=-50 m的面只约束y方向位移，在模型底面只约束z方向位移。

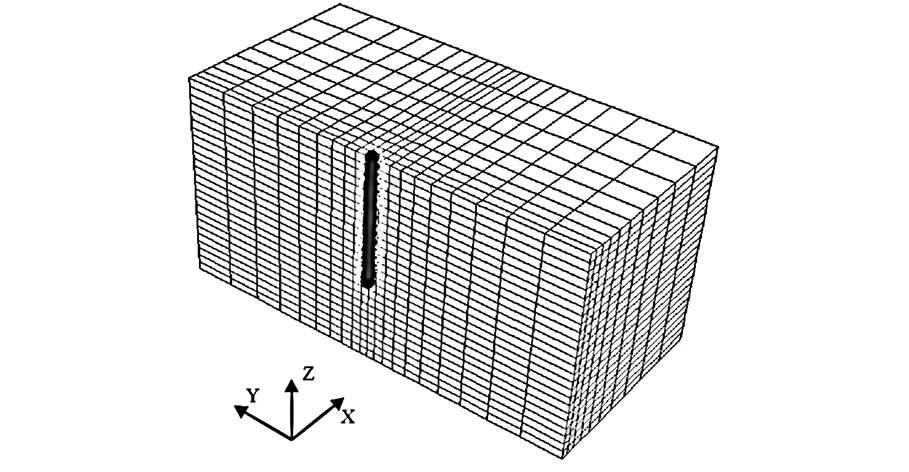
图5 FLAC模型(半模型)

对于桩土界面初始刚度的确定，采用Alonso提出的方法，本例的计算中取Δu=12 mm。双曲线模型和理想弹塑性模型除耦合弹簧刚度不同之外，其他参数均一样。

分别采用理想弹塑性模型和双曲线模型所计算出的桩顶处的荷载-沉降(P-S)曲线与Guo和Randolph[9]结果的对比如图6所示。

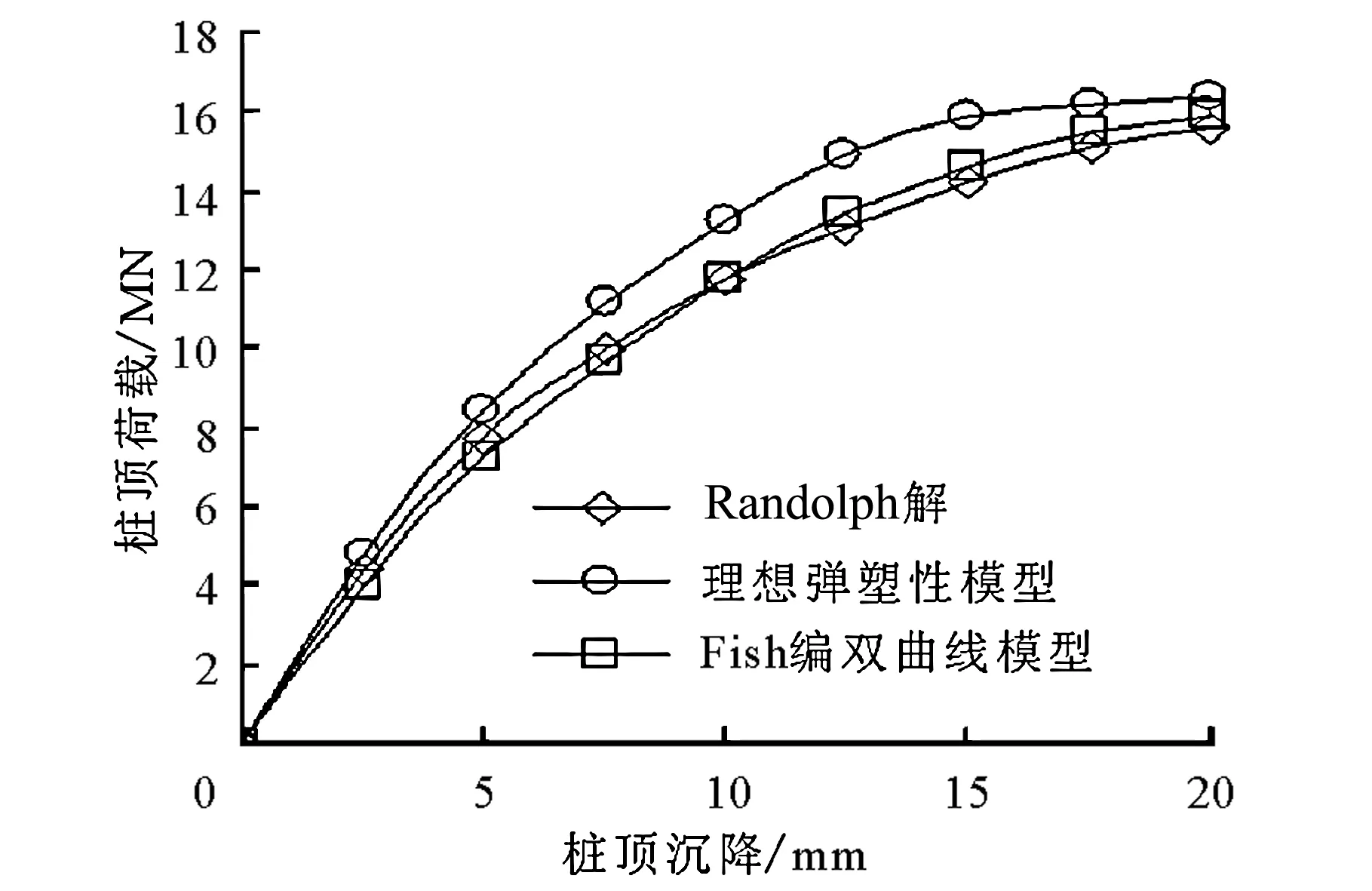
图6 桩顶荷载-沉降曲线

由图6可看出，当采用相同的初始刚度时，在相同的荷载作用下，理想弹塑性模型计算的沉降值比Randolph解计算的沉降值偏小，而双曲线模型计算的沉降值则与Randolph解的结果非常吻合。

由此可见，本文所编的FISH程序成功地实现了用双曲线模型替换内嵌的理想弹塑性模型，前者更好地反映了桩土界面的非线性特性，提高了计算的准确性。采用双曲线形式的荷载传递函数比采用理想弹塑性形式的荷载传递函数能更好地模拟桩土相互作用。此外，将Alonso所提出的确定桩土界面的初始剪切刚度的方法应用到FLAC3D中是可行的，该方法不仅为确定桩土界面的初始剪切刚度提供了合理的参考，而且能够考虑土的深度效应对桩土界面刚度的影响。

5 结 语

本文以有限差分软件FLAC3D为平台，提出可考虑桩土相对滑移和土体深度效应的改进双曲线模型，并利用FLAC3D内嵌的FISH汇编语言编程，将改进双曲线模型应用到FLAC3D的桩土相互作用的分析中。最后，将本文方法的计算值、FLAC3D内嵌理想弹塑性模型的计算值与实例进行对比。结果表明：本文提出的改进双曲线模型能够较好地应用到数值模拟中，它能够更为合理准确地模拟桩土共同作用。

[1] Seed H B, Reese L C. The action of soft clay along friction piles[J]. Transaction， ASCE, 1955, 122: 731-754.

[2] Kezdi A. The bearing capacity of piles and pile groups[C]// 4th International Conference on Soil Mechanics and Foundaiton Engineering. London, 1957: 46-51.

[3] Vijayvergiya V N. Load-movement characteristics of piles[J]. Coastal and Ocean Division, ASCE, 1977，(2): 269-284.

[4] 辛公锋. 大直径超长桩侧阻软化试验与理论研究[D]. 杭州: 浙江大学, 2006.

[5] 陈龙珠, 梁国钱. 桩轴向荷载-沉降曲线的一种解析算法[J]. 岩土工程学报, 1994, 16(6): 30-38.

[6] 陈明中. 群桩沉降计算理论及桩筏基础优化设计研究[D]. 杭州: 浙江大学, 2000.

[7] 张忠苗. 桩基工程[M]. 北京: 中国建筑工业出版社, 2007.

[8] Alonso E E, Josa A, Ledesma A. Negative skin friction on piles: A simplified analysis and prediction procedure[J]. Geotechnique, 1984, 34(3): 341-357.

[9] Guo W D, Randolph M F. Vertically loaded piles in non-homogeneous media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21: 507-532.

[10]Wong K S, Teh C I. Negative skin friction on piles in layered deposits[J]. Journal of Geotechnical Engineering, ASCE, 1995, 121(6): 457-465.

[11]Poulos H G, Davis E H. Pile Foundation Analysis and Design[M]. New York: John Wiley & Sons, 1980.

[12]罗 斌, 凌 辉, 李 熹. 单桩荷载传递双曲线模型的研究[J]. 建筑技术开发, 2004, 31(l): 29-31.

[13]Desai C S, Drumm E C. Cyclic testing and modeling of interface[J]. Journal of Geotechnical Engineering, 1985, 111(6): 793-815.

[14]Uesugi M, Kishida H, Tsubakihara Y. Friction between sand and steel under repeated loading[J]. Soils and Foundations, 1989, 29(3):127-137.

[15]Yin Z Z, Zhu H, Xu G H. A study of deformation in interface between soil and concrete[J]. Computers and Geotechnics, 1995, 17(1): 75-92.

[16]Randolph M F, Wroth C P. Analysis of deformation of vertically loaded piles[J]. Journal of Geotechnical Engineering Division, ASCE, 1978,104: 1465-1488.

[17]陈仁朋, 周万欢, 曹卫平,等. 改进的桩土界面荷载传递双曲线模型及其在单桩负摩阻力时间效应研究中的应用[J]. 岩土工程学报, 2007, 29(6): 824-830.