线荷载作用下混凝土双向板的挠度分析

张先进， 石 俊, 陈 浩

(1.华中科技大学 a.土木工程与力学学院; b.控制结构湖北省重点实验室， 湖北 武汉 430074；2. 武汉宝安房地产开发有限公司， 湖北 武汉 430079)

钢筋混凝土双向板在工业与民用建筑中应用十分广泛，随着板的应用跨度日益增大，常常遇到板上作用有集中线荷载的情况，如隔墙等，此时预测板在正常使用阶段的挠度对指导工程设计具有重要的意义。

在计算钢筋混凝土双向板的挠度时，有两个方面的问题需要解决：(1)确定位移函数；(2)确定适当的抗弯刚度。

对钢筋混凝土双向板而言，确定适当的抗弯刚度比梁更为困难。虽然文氏[1]等人提出了如下经验方法：当荷载较小(裂缝出现前)时，按毛截面计算EI值，当荷载较大(裂缝出现后)时，按换算截面计算EI值，但实际情况表明，这不能从根本上解决板在使用阶段的挠度计算问题。

1 双向板位移函数的选取与确定

1.1 四边简支板

四边简支矩形钢筋混凝土板的计算简图如图1所示，板沿x、y方向的边长分别为a、b，板厚h，在跨中(0≤x≤a，y=b/2)处作用有垂直于板面向下、大小为q0的线荷载。视混凝土双向板为双向正交异性板，由于变形的连续性，必存在一个连续的位移函数。

图1 简支双向板计算简图

设位移函数：

(1)

式中，D为待定位移系数。显然，该函数满足四边简支板的边界条件。

根据小挠度板理论[2～4]，板的内部虚功：

式中，B0为四边简支板的短期抗弯刚度，将式(1)代入上式中，可得

(2)

考虑板面同时作用有线荷载q0和均布活荷载q′，则线荷载q0的外部虚功：

(3)

其中L为积分路径：0≤x≤a，y=b/2。

均布荷载q′的外部虚功：

(4)

其中Ω为积分区域：0≤x≤a，0≤y≤b。

总外虚功为：

(5)

由虚功原理[5]可得：

(6)

令n=b/a，记K0=B0(n4+2n2+1)为四边简支双向板的整体刚度特征系数，则

(7)

将式(7) 代入式(1)，得位移函数：

(8)

1.2 四边固支板

四边固支矩形钢筋混凝土板的计算简图如图2所示，板沿x、y方向的边长分别为a、b，板厚h，在跨中(0≤x≤a，y=b/2)处作用有垂直于板面向下、大小为q0的线荷载。

设位移函数：

(9)

式中，D为待定位移系数。显然，该函数满足四边固支板的边界条件。

(10)

图2 固支双向板计算简图

考虑板面同时作用有线荷载q0和均布活荷载q′，则荷载总外虚功为：

(11)

由虚功原理可知：

(12)

令n=b/a，记K=B(3n4+2n2+3)为四边固支双向板的整体刚度特征系数，则

(13)

将式(13) 代入式(9)，得位移函数：

(14)

2 双向板的抗弯刚度与挠度计算

我国《混凝土结构设计规范》[6]中只给出了钢筋混凝土单向受弯构件的刚度计算公式，考虑双向板双向弯曲和受压区混凝土双向受压的特点，本文根据张平生等人的研究结果[7～9]，在《混凝土结构设计规范》的刚度计算公式中引入双向板刚度特征系数φ，得到四边简支双向板的短期抗弯刚度计算公式：

(15)

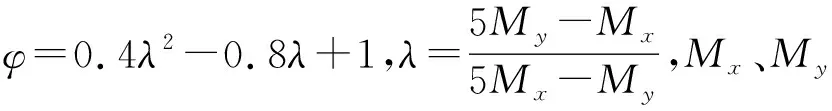
对四边固支混凝土双向板而言，在垂直于板面的竖向荷载作用下，支座截面承受负弯矩，跨中截面承受正弯矩。那么在计算挠度时应根据哪一截面计算板的抗弯刚度是个不易确定的问题。因此，本文试图根据四边固支与四边简支的双向板挠度之间的关系，建立四边固支板的挠度计算方法。

点曲线的使用方式完全不同。我们可以在曲线的任意位置上单击创建调整垫，并且随心所欲拖动；接着还可以继续创造更多新的调整垫。但无论点曲线还是参数曲线，始终不变的是左下角对应暗部，右上角对应亮部。向上拖动右侧向下拖动左侧就能得到提高反差的S形曲线。

在相同荷载条件下，四边固支与四边简支双向板挠度之间的关系如图3所示。f1为四边固支板反弯点处的挠度，f2为弯点迹线所围成的四边简支板的最大挠度。

图3 四边固支板跨中板带的受力与变形

为简化计算，假定f1沿反弯点迹线等值(事实上，f1在反弯点迹线所围成的矩形角点处较小，矩形边长中点处较大)。试算结果表明，由此引起的对整体挠度的误差并不大。则四边固支板的最大挠度为：

f=f1+f2

(16)

(17)

当仅有均布荷载作用时，取π2≈10，则

(18)

对四边简支板

(19)

对四边固支板

(20)

3 计算结果分析与比较

计算模型1采用边长为 6000 mm、板厚130 mm的钢筋混凝土方板，在跨中作用有与x轴平行的集中线荷载，板面均布荷载仅考虑板的自重。混凝土强度等级为C20，泊松比v=0.2，钢筋为Ⅰ级，受拉钢筋配筋率ρx=ρy=0.7%，四边固支时支座负筋的配筋率为0.7%。在应用ANSYS软件进行有限元分析时，采用分离式模型，混凝土单元选用Solid65，钢筋单元选用Link8，混凝土的本构关系为：

σ=fc[1-(1-εc/ε0)2]εc≤ε0；

σ=fcε0<εc≤εcu

式中，ε0=0.002，εcu=0.0033。

钢筋的本构关系为：σ=Esεs≤fy。

应用本文公式和ANSYS软件的计算结果如图4、图5所示，二者吻合较好。

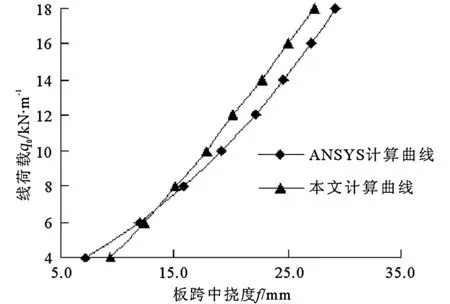
图4 四边简支板荷载—挠度曲线

图5 四边固支板荷载—挠度曲线

计算模型2为板跨中作用有线荷载8 kN/m(相应于200 mm厚轻质砌块墙体自重)，n=0.6，材料强度、板厚及配筋同计算模型1，四边固支时支座负筋的配筋率为0.7%。按本文公式得到的板跨中挠度与线荷载作用位置及板短边尺寸的关系见图6。线荷载沿板长跨方向布置，不同n值时板跨中挠度与板短边尺寸的关系见图7。

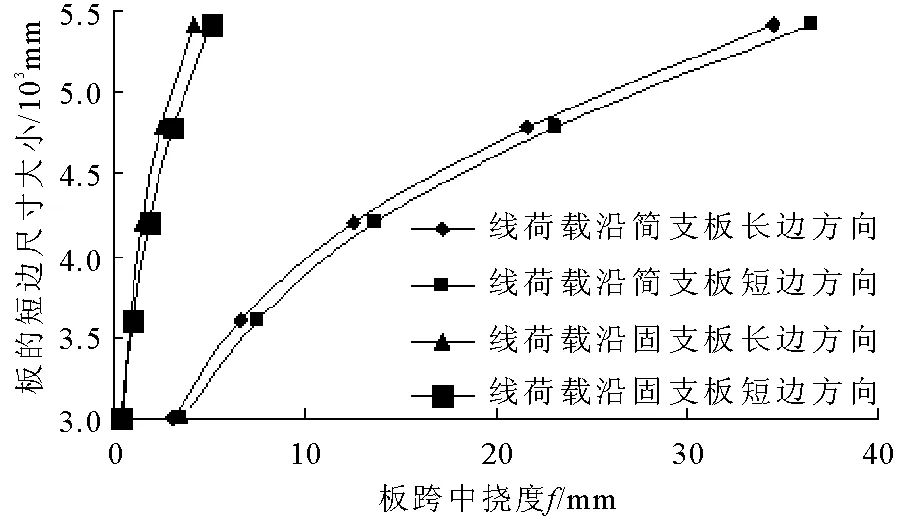
图6 不同线荷载作用位置板的短边尺寸—挠度曲线(n=0.6)

图7 不同n值板的短边尺寸—挠度曲线

计算模型3为板跨中作用有线荷载8 kN/m且沿板长跨方向布置，板长边为 6000 mm，n=0.6，材料强度及配筋同计算模型2，按本文公式得到的板跨中挠度与板厚的关系见图8。改变配筋率的大小可得板跨中挠度与配筋率的关系见图9。

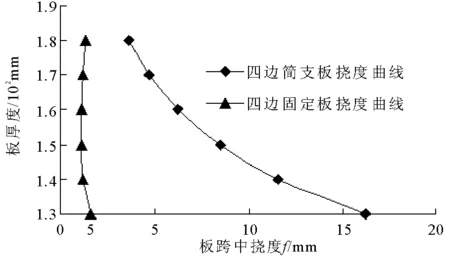
图8 板厚—挠度曲线

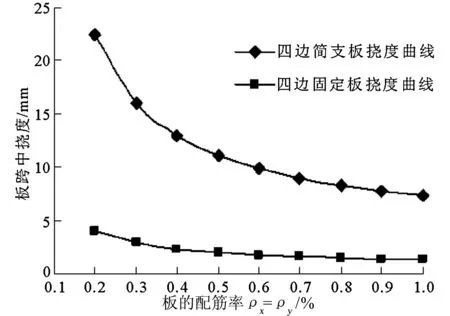
图9 板的配筋率—挠度曲线

混凝土板在长期荷载效应作用下的挠度可利用式(15),按《混凝土结构设计规范》的方法计算长期抗弯刚度，然后由式(17)～(20)计算长期挠度。

4 结 论

(1)本文研究了有线荷载作用的混凝土双向板在正常使用阶段的挠度计算方法，并根据相同荷载条件下四边固支与四边简支板的挠度关系，导出了四边固支板的抗弯刚度公式，反映了板的抗弯刚度的非线性特征。其计算结果与板的实际受力特性相符，且和大型商用软件ANSYS的计算结果吻合较好。

(2)分析结果表明，板面线荷载的作用位置、双向板的长短边尺寸和板厚对板的挠度有较大影响；跨中线荷载沿板短跨方向布置时较为有利；板的挠度随长短边尺寸的增大而增大，且短边相同时，短边与长边之比越小，挠度越大；板的挠度随板厚的增大而显著减小。

(3)当ρx=ρy<0.5%时，配筋率对板的挠度有较大的影响；当ρx=ρy≥0.5%时，配筋率对板的挠度的影响逐渐减小。

(4)在同等条件下，与四边固支板相比，四边简支板的挠度相对较大，且对上述各参数变化的反应更加敏感。

[1] Gamble W L. Moments in beam supported slabs [J]. J Am Concr Inst, 1972, 69(3), 149-157.

[2] (美) R·派克, W·L·根勃尔. 钢筋混凝土板[M]. 黄国桢, 成源华译. 上海: 同济大学出版社, 1992.

[3] 曲庆璋, 章 权, 季求知,等. 弹性板理论[M]. 北京: 人民交通出版社, 2000.

[4] 黄 炎. 弹性薄板理论[M]. 湖南: 国防科技大学出版社, 1992.

[5] 龙驭球, 包世华. 结构力学[M]. 北京: 高等教育出版社, 2000.

[6] GB J50010-2002,混凝土结构设计规范[S].

[7] 张平生. 四边简支钢筋混凝土双向板挠度计算与板厚确定[J]. 西安冶金建筑学院学报, 1991,(3):14-17.

[8] Nawy E G. Flexural cracking in two-way concrete slabs reinforced with high strength weld wire fabric[J]. ACI, 1964,(8): 54-61.

[9] 丁大钧. 现代混凝土结构学[M]. 北京: 中国建筑工业出版社, 2000.