古建筑木构架抗震性能试验＊

周 乾,闫维明,张 博

(1.北京工业大学工程抗震与结构诊治北京市重点实验室,北京 100124;2.故宫博物院,北京 100009)

0 引言

我国的古建筑以木结构为主,梁与柱采用榫卯节点形式连接。地震作用下,榫头和卯口之间相互挤压和摩擦可耗散部分地震能量,从而减小结构的破坏。一些学者对古建筑榫卯节点的抗震性能进行了研究,如文献[1-2]以穿斗式柱梁节点为对象,通过加载试验研究了不同形式榫卯节点的破坏模式,总结出节点的M-θ回归方程表达式;文献[3-4]对1∶3.52缩尺比例的2等材木构架平面框架模型进行了低周水平反复荷载试验,获得了榫卯节点的抗震性能。为研究考虑榫卯连接的古建筑木构架的抗震性能,本文将基于上述成果,建立考虑榫卯连接的4梁4柱古建筑木结构空间模型,通过进行低周反复加载试验来分析构架的抗震参数和恢复力模型,结果将为古建筑保护提供理论参考。

1 试验方案

模型以现存故宫太和殿某开间尺寸为原型,参照清式《营造则例》相关规定,制作成4梁4柱结构[5],榫卯节点为承重构架常采用的燕尾榫节点形式。模型共3组,考虑制作安装、加载等各项误差因素,缩尺比例取1∶8。为了方便加载,基于已有的试验成果,柱头截面高出额枋150 mm[6-7]。构件的具体尺寸见图1所示。

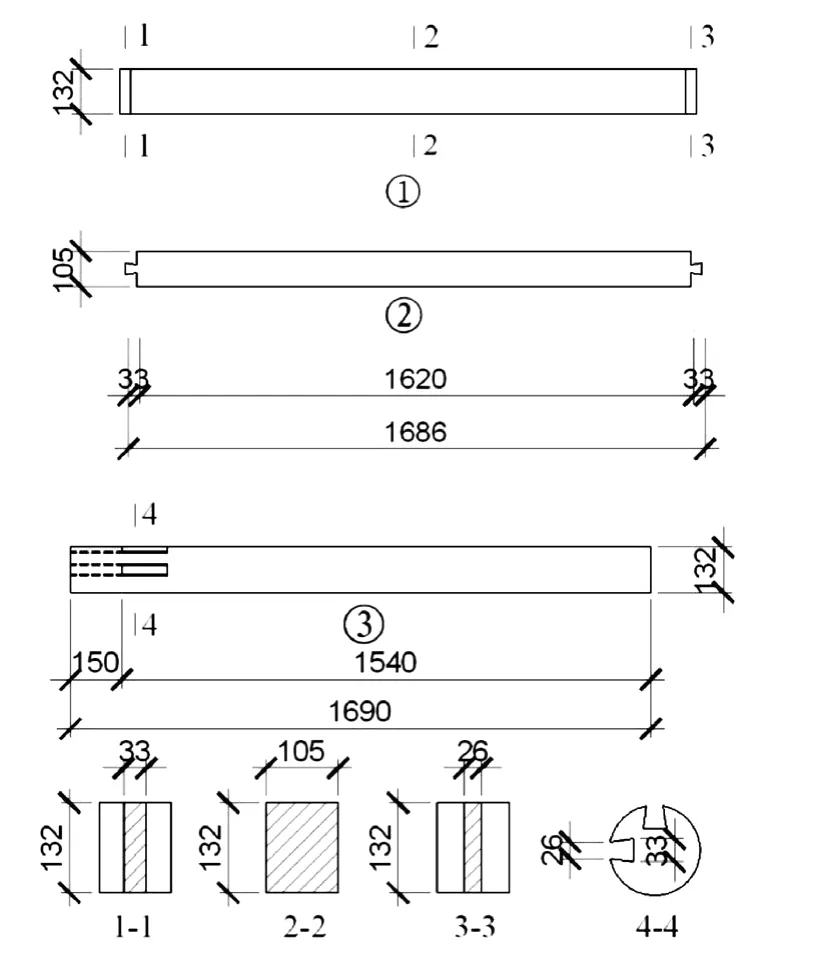
图1 构件尺寸(单位:mm)

试验时,采用支座考虑为单向铰支座模拟柱础,铰的转动方向与加载方向相同。考虑到所需的外力不是很大,试验采用手动加载方式,通过自制的加载装置对构架加载。另屋顶采用混凝土板模拟。根据对太和殿屋顶分层构造的勘查结果,求出三次间屋顶的实际重量,按相似比计算得混凝土板重量为1.03 t,安装方式为浮放在柱顶。为增加屋面板与柱顶之间的摩擦力,屋面板底部尽量粗糙。为防止试验过程中构架侧移过大导致屋面板发生落架,试验前用吊车将屋面板通过吊绳轻轻套住以保证试验安全。

为了获得构架的侧移,在每根柱子的上侧沿受力方向布置了±200 mm量程的位移计(编号W1-W4);为了测定节点弯矩,在每根柱子的内外侧分别布置了电阻应变片(编号Z1-Z8);为了测定榫卯节点转角,在沿受力方向的两根梁的上下端部布置了两个量程为±100 mm的位移计,通过上下位移计的读数来获得节点转角(编号Wa-Wh);考虑所需的外力不大,选用的力传感器的吨位控制在1 t。构架测点布置见图2所示。

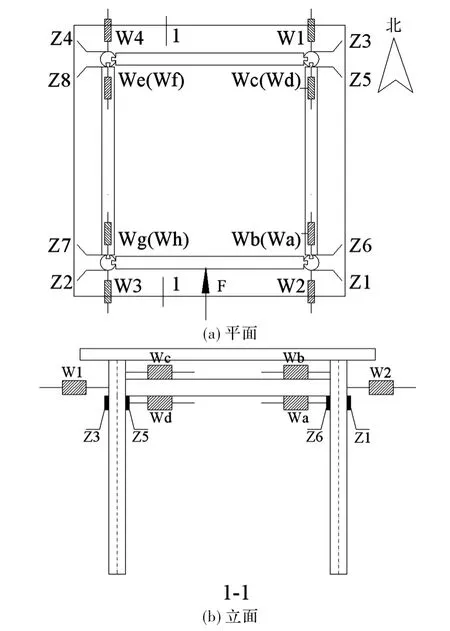
图2 测点布置(Z表示应变片,W表示位移计)

参考相关试验成果[8],本试验采用变幅位移控制的加载方式,加载的位移控制值为0、±30 mm、±60 mm、±90 mm、±120 mm、±150 mm,每级位移循环一次。为了详细观察试验过程中模型构架的变形及榫卯节点破坏状况,在每级加载过程中,构架的侧移达到控制值时,对构架整体及节点上下端的变形和破坏情况进行拍照分析,同时根据试验具体情况修正试验方案,如调整加载速率,控制结构位移幅值等。

2 试验现象

加载过程中,构架节点位置有吱声,且随着构架侧移增大,吱声由间断变得连续而有节奏,反映了榫卯节点转角增大后榫卯之间的咬合程度越来越大。施加外力时,在构架侧移较大时所需的外力较大,随后立刻减小,尤其在平衡位置附近,似乎构架不需推力自行能向平衡位置移动;过平衡位置后,外力又开始增大,节点开始不断发出吱声且富有节奏。这说明构架侧移大时,柱头偏心矩大,节点转角大,榫卯咬合紧密,要使节点转角及构架侧移恢复必须使较大外力;而当构架侧移逐步减小时,柱头偏心矩及节点转角均减小,构架恢复力增大,且由于榫卯之间的相互滑移作用,使得构架在平衡位置附近移动是所需的外力很小。

此外,在加载过程中榫卯节点有拔榫现象。构架被推时节点上端拔榫下端挤紧,被拉时下端拔榫上端挤紧,且随着构架侧移值的增大,节点拔榫量也增大。由此可知对构架进行水平推拉时,榫头主要表现为绕卯口转动,且转角随着构架侧移增大而增大。当水平拔出力大于卯口对榫头的嵌固力时,榫头绕卯口转动的同时,还要产生拔榫。

构架在受拉150 mm时的侧移情况及节点拔榫情况见图3所示。

图3 变形照片(Δ=150 mm)

3 试验分析

3.1 P-Δ滞回曲线

构架在水平荷载作用下的滞回曲线是其抗震性能的一个综合体现,能反映结构的承载力、抗裂度、变形能力、耗能能力、刚度及破坏机制等。一般来说,滞回环面积越大,说明构架的耗能能力越强。基于试验结果,获得了3组构架共的PΔ曲线见图4所示。

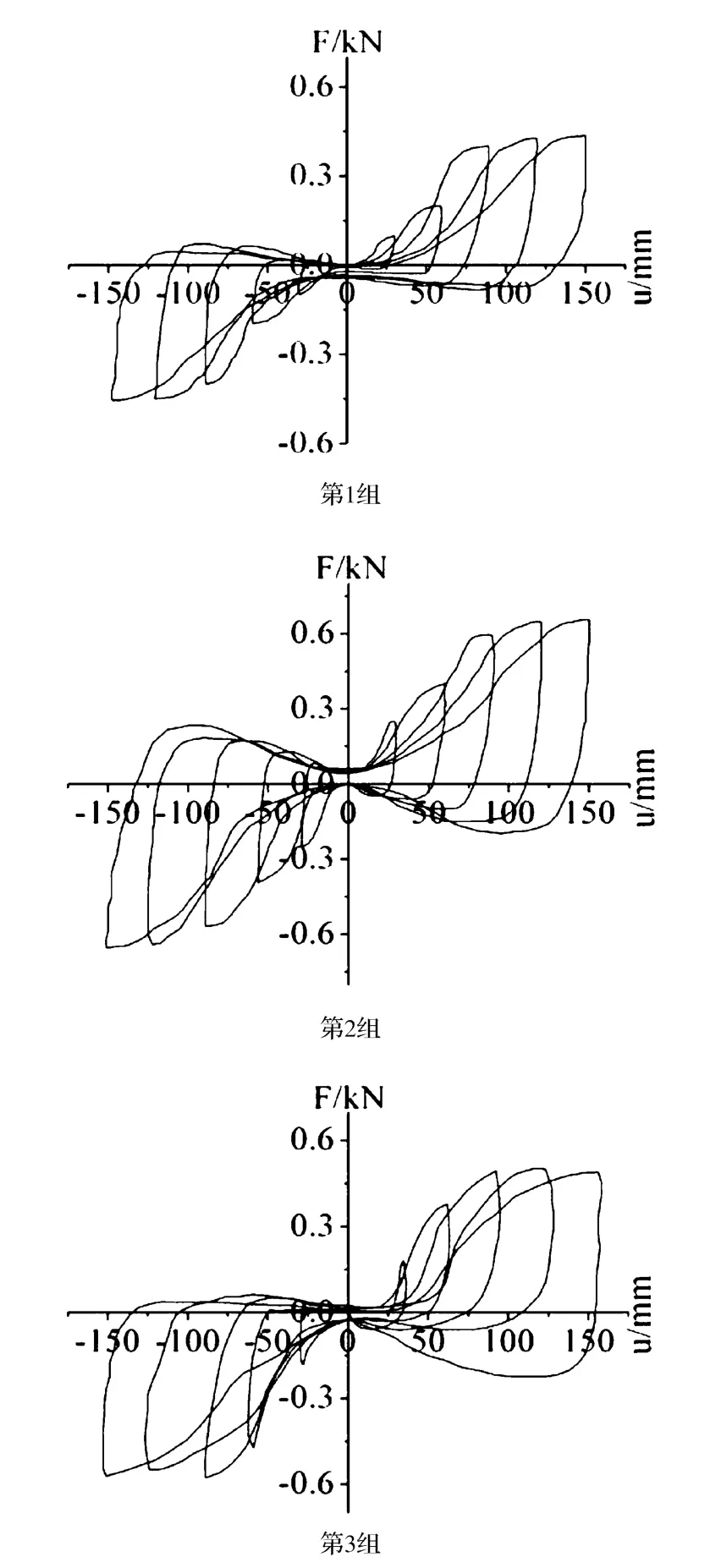
图4 构架P-Δ滞回曲线

易知可知构架的P-Δ滞回曲线具有如下特点:①构架滞回曲线为Z形。这说明榫卯节点在受力过程中有较大的滑移,且随着构架侧移增大,节点在平衡位置附近的滑移量也增大;②从每次加载循环曲线看,构架侧移较小时,曲线基本与x轴重合,说明这个过程是榫卯节点由松弛状态挤紧发展,节点耗能能力较弱供;而随着构架侧移增大,榫头与卯口相对转角增大,榫头开始产生拔榫,滞回环形状外鼓,即节点耗能能力增强,此时构架承载力由榫卯节点提供;另一方面,随着构架侧移增大,柱头上荷载产生的偏心矩也增大,使得构架侧移较大时,滞回曲线斜率变缓;当构架达到控制位移时卸载,变形并不能恢复,必须反向加载才能实现,这说明榫卯节点的恢复力较小,构架的塑性变形需要外力恢复;③刚开始加载时,构架侧移小,榫卯在外力作用下开始挤紧且产生相对滑移;随着荷载增加,榫卯之间滑移距离增加,且开始产生相对转动,在构架屈服前滞回曲线基本为直线;随着荷载不断反复作用,榫头逐渐从卯口拔出,表征刚度变化的滞回曲线斜率逐渐下降,表明构架刚度降低,并带有较大的滑移和剪切变形影响。④构架滞回环较饱满,且随着侧移增大而外鼓,反映了构架的耗能性能较好;滞回环左右两部分基本相同,反映了构架受推及受拉过程的耗能能力基本相同。

另构架滞回曲线图形并不完全对称,大概有如下几个原因:①木构架及榫卯节点制作、安装的尺寸误差;②木材材料的各向异性,各构架破坏形式不一定完全相同;③榫卯节点间的干摩擦效应不一致。

3.2 骨架曲线

根据构架P-Δ滞回曲线可获得相应的骨架曲线,见图5(a)所示,其中Gi(i=1～3)表示第i组,下同。

为了消除试验数据的离散性和随机因素的不确定性,对图5(a)中3条骨架曲线的峰值点取均值,以获得具有一般规律的骨架曲线,结果表明均值曲线的形状为S形。考虑榫卯节点的受力特点及强度退化,采取Boltzmann方程对平均值曲线进行拟合后,获得构架的P-Δ一般性骨架曲线见图5(b)所示,其中ave表示平均值点(下同),fit表拟合曲线。曲线的拟合方程为:

式中:F为外力;x为构架侧移;R-Square为拟合优度系数;F=0.6 kN和F=-0.63 kN为拟合曲线的上下渐进线。由拟合优度系数可知骨架曲线与所得方程几乎完全正相关。另由拟合方程可知,节点在构架屈服以前,构架外力随着侧移增大而增大,曲线形状比较平缓,反映了构架良好的延性。

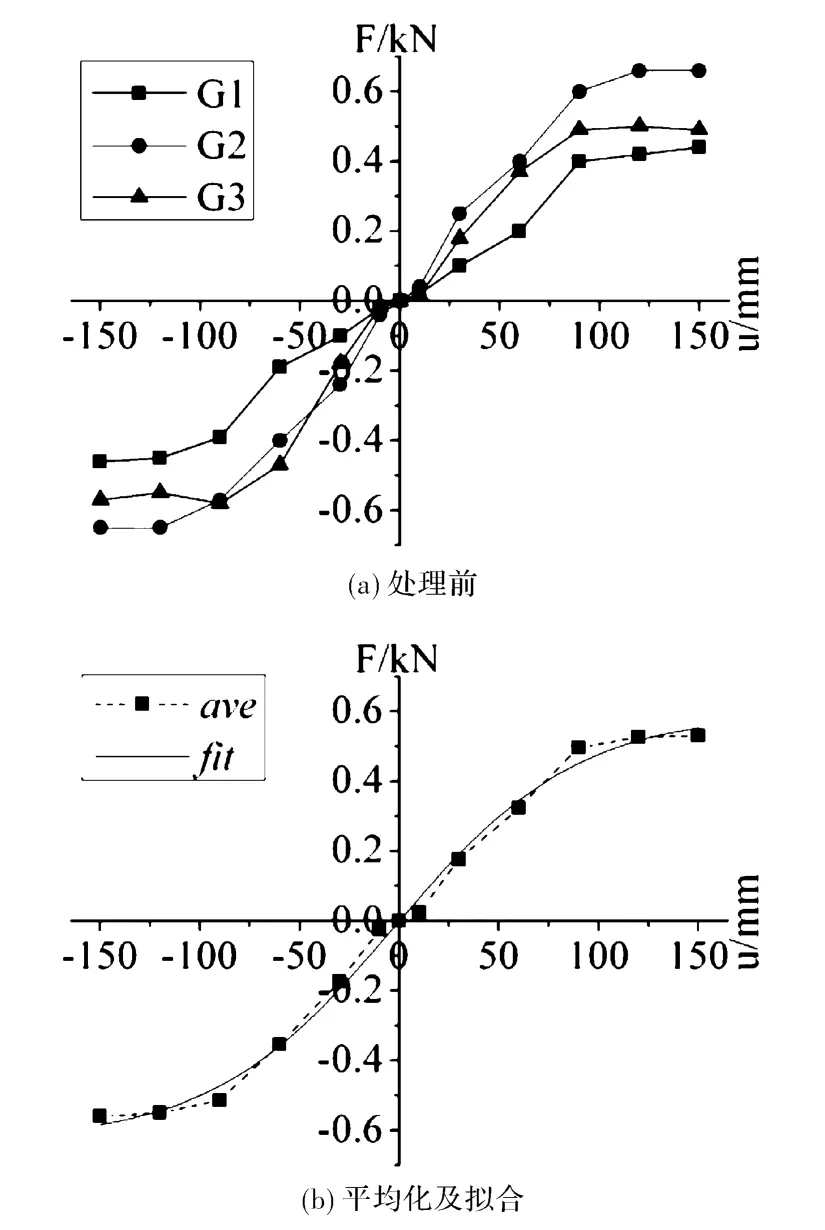
图5 骨架曲线

构架P-Δ骨架曲线具有如下特点:

(1)可以看出骨架曲线具有滑移段、弹性段、强化段和屈服段的特征。开始阶段,榫卯有相对滑移,主要是因为榫头和卯口之间有空隙,但滑移表现不明显,滑移长度约为10 mm;随后,榫头和卯口开始咬合,构架刚度增大,在构架侧移为30 mm时,曲线斜率较大,构架处于弹性段,此时的荷载约为最大值的30%;随后曲线变缓,榫卯节点相对转角增大,提供构架的承载力增强;另一方面,构架侧移增大使得柱头上荷载产生的偏心矩增大;当构架侧移达到90 mm时,曲线开始出现较为明显的转折,反映了构架进入屈服阶段,此时的荷载约为最大荷载的80%;当构架侧移达到150 mm时,曲线出现了承载力下降趋势,柱头上荷载产生偏心矩过大导致曲线更加平缓,外力最大均值达到0.55 kN。

(2)构架的骨架曲线相对比较平缓,反映了构架有较好的延性。

3.3 构架耗能

本文采用等效粘滞阻尼系数he来表示木构架的耗能能力[9],值越大表示耗能能力越强。分别求出各构架在每个加载循环过程中的he值,绘出he-Δ均值曲线见图6所示。

图6 构架耗能曲线

易知构架的he值随着构架侧移增大呈逐增大而又趋于稳定,这是因为构架侧移增大时,榫卯之间的滑移摩擦距离越大,咬合程度加深,节点转角增大,在榫头完全拔出卯口之前,构架的耗能能力得到了提高。

3.4 刚度退化

在水平荷载作用下,构架刚度随着循环周数和控制位移增大而减小,即产生刚度退化。构架侧移在每次达到控制位移时的刚度可按下式计算[10]:

式中:ki为第i级荷载作用下构架的侧移刚度;Pi为第i级荷载峰值;Δi为第i级峰值荷载对应的构架侧移。

分别对3组构架计算每一级加载循环下的刚度值(单位:kN/mm),绘出构架侧移刚度退化曲线见图7所示。易知在构架侧移较小时,构架刚度较大,此时节点尚处由松至紧状态;随着构架侧移增大,榫卯间相对滑移距离增长,节点产生拔榫,构架刚度降低;当构架侧移越来越大时,由于柱头上屋面板荷载产生偏心矩增大,使得构架刚度降低明显。

图7 构架刚度退化曲线

3.5 延性系数

构架的抗震性能主要从强度、刚度、变形能力及耗能能力进行评价,而构架的变形能力可用延性系数表示。本试验中,构架延性系数可按如下公式计算:

式中:μ为构架延性系数;Δu为构架极限位移,Δu=150 mm;Δy为构架屈服位移,当构架屈服点不明显时,可采取图8所示方法取值[9]。

图8 屈服点确定方法

在图8中过原点O做直线OA将骨架曲线分成Ι、П两部分且它们的面积相等,点A在过极限荷载点C的水平线上,过点A做垂线与骨架曲线相交与点B,点B即为近似屈服点。

对3组构架试验数据进行分析,求得构架的延性系数见表1所示。

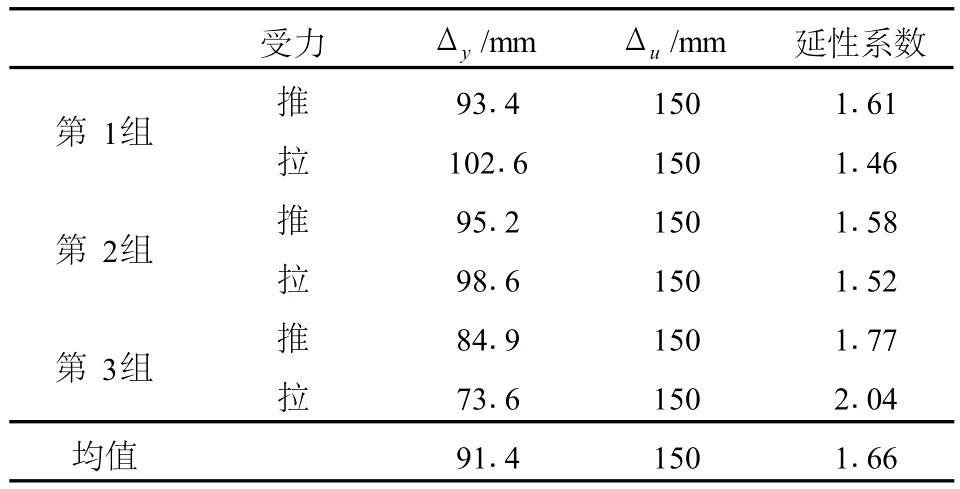
表1 构架延性系数

3.6 恢复力模型

本文采用试验拟合法来确定木构架的P-Δ恢复力模型,主要做法为:根据试验获得的相关数据绘制曲线,然后利用一定的数学模型进行拟合,确定骨架曲线和不同控制下的标准滞回环,再将骨架曲线和各标准滞回环结合起来组成恢复力曲线,并利用不同控制变形下的标准滞回环相比较确定反复加载时的刚度退化规律。

(1)骨架曲线:根据试验获得的构架滞回曲线及骨架曲线,可把木构架恢复力模型的骨架曲线理想化为三线段曲线,即滑移段、弹性段、屈服段,见图9所示。

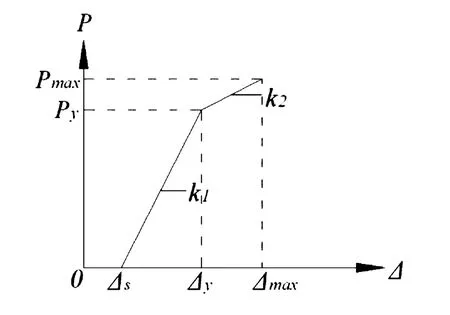
图9 骨架曲线模型

图9中,Δs为构架滑移的位移;Δy、Py分别为构架屈服时的位移及对应荷载,其中Δy按表1取值;Δmax、Pmax分别为构架最大位移及对应荷载,本试验中取Δmax=150 mm[10];k1、k2分别为骨架曲线各段刚度,k1=Py/(Δy-Δs),k2=(Pmax-Py)/(Δmax-Δy)。基于对各组数据进行分析并取平均值,求得:k1=0.006 2kN/mm,k2=0.000 84 kN/mm。

(2)滞回规则:正向加、卸载曲线为图10中A-B-C-D-E-F段:AB段可认为是滑移段,刚度为0;从D点卸载时,卸载直线段DE刚度较大;由于构架残余变形的存在,卸载后需要反向加载方可使构架变形恢复;反向加载直线段EF基本与x轴平行,且向原点靠拢。反向加、卸载曲线为图10中A-b-c-d-e-f段,正、反向加载卸载曲线对称。

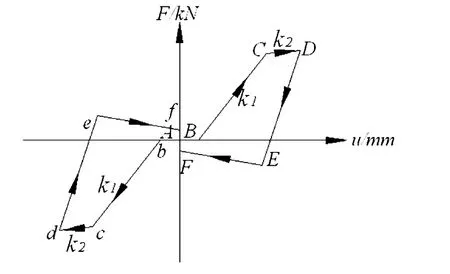
图10 构架力-侧移恢复力曲线

4 结论

(1)古建筑木构架P-Δ滞回曲线为Z形,具有明显的捏拢特性。

(2)构架的骨架曲线具有滑移段、弹性段、强化段和屈服段的特征,且骨架曲线平缓,反映了构架较好的变形能力。

(3)在榫头完全拔出前,构架等效粘滞阻尼系数值随着构架侧移增大增大而趋于稳定。

(4)构架侧移刚度随构架侧移增大有减小趋势。

[1] Chang Wen-Shao,Hsu Min-Fu,Komatsu Kohei.Rotational performance of traditional Nuki joints with gap I:theory and verification[J].Journal of Wood Science,2006,52:58-62.

[2] Chang Wen-Shao,Hsu Min-Fu.Rotational performance of traditional Nuki joints with gap II:the behavior of butted Nuki joint and its comparison with continuous Nuki joint[J].Journal of Wood Science,2007,53:401-407.

[3] 高大峰,赵鸿铁,薛建阳,等.中国古建木构架在水平反复荷载作用下的试验研究[J].西安建筑科技大学学报:自然科学版,2002,34(4):317-324.

[4] 赵鸿铁,张海彦,薛建阳,等.古建筑燕尾榫节点刚度分析[J].西安建筑科技大学学报:自然科学版,2009,41(4):450-454.

[5] 宾慧中,路秉杰.浅识宋材份制与清斗口制[J].安徽建筑,2003(3):1-2.

[6] 谢启芳,赵鸿铁,薛建阳,等.中国古建筑木结构榫卯节点加固的试验研究[J].土木工程学,2008,41(1):28-34.

[7] 于业栓,薛建阳,赵鸿铁.碳纤维布及扁钢加固古建筑榫卯节点抗震性能试验研究[J].世界地震工程,2008,24(3):112-117.

[8] 葛鸿鹏.中国古代木结构建筑榫卯加固抗震试验研究[D].西安:西安建筑科技大学,2004:32-33.

[9] 李忠献.工程结构试验理论与技术[M].天津:天津大学出版社,2003.

[10]谢启芳.中国木结构古建筑加固的试验研究及理论分析[D].西安:西安建筑科技大学,2007.