关于二阶变系数线性微分方程求解法的研究
2010-01-18常秀芳
李 高,常秀芳
(大同大学煤炭工程学院,山西大同037003)
国内外现行《高等数学》中的方程[1],只是对常系数微分方程的情况做了详细的讨论,即使《常微分方程》也未对二阶变系数微分方程的解作进一步的阐述.
若 p(x)、q(x)为连续非常数的函数,方程

则称为二阶变系数线性微分方程.如果f(x)恒等于零,那么该方程称为二阶变系数齐次线性微分方程;如果f(x)不恒等于零,那么该方程称为二阶变系数非齐次线性微分方程.
对一般的二阶变系数线性微分方程而言,由《常微分方程》教材[2]知,只要能求出二阶变系数齐次线性微分方程的一个特解,则二阶变系数线性齐次或非齐次微分方程的解即可求得.尽管专家学者目前的研究[3-4]给出了特殊类型的二阶变系数线性微分方程的求解法,然而到目前为止,如何求出其中的某一特解是无法可循的.那么如何求其解是要研究的对象.本文利用构造法在求二阶变系数线性微分方程的通解的一般方法上进行探讨,诣在解决二阶变系数线性微分方程求解的问题,并得出成规求解的方法与结论,以便适应在工程技术的实际领域或学生在学习相关专业中的需要.
1 二阶变系数线性微分方程的一般求解法
假设二阶变系数非齐次线性微分方程中 p(x)具有一阶连续的导数、q(x)连续.
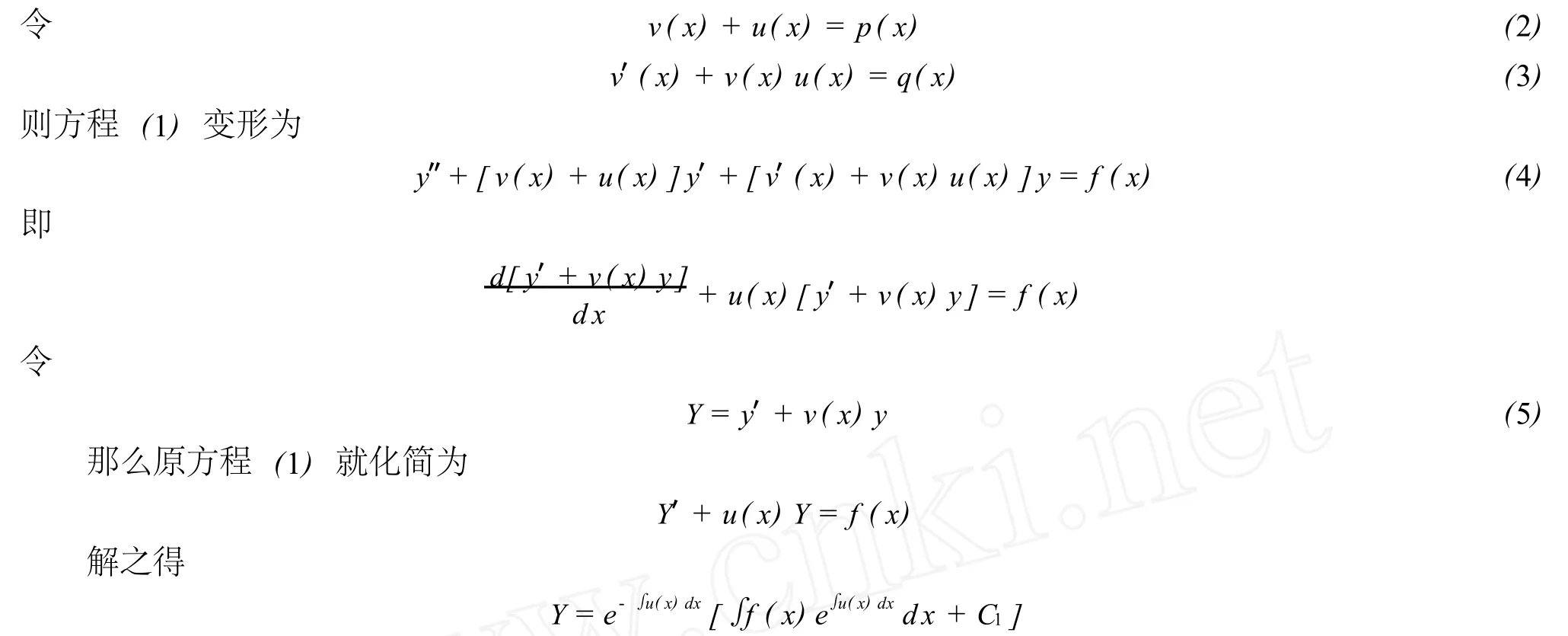
将之代入 (5)式.则方程 (1)通过上述变换可降阶为
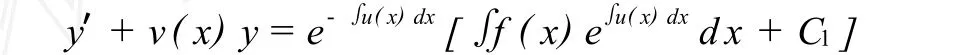
此一阶线性非齐次微分方程的解就是我们所要求的二阶变系数非齐次线性微分方程的解[5].而方程
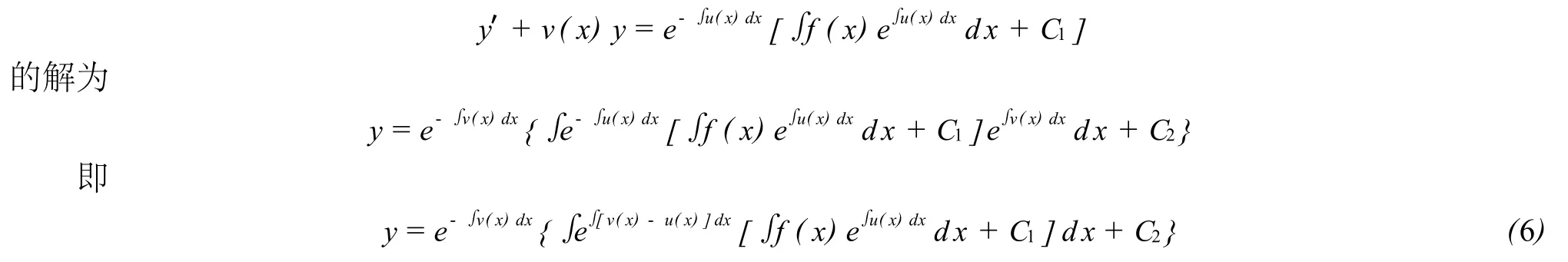
故式 (6)为二阶变系数非齐次线性微分方程

特别地1 当 f(x) ≡0时,方程 (1)就转化为二阶变系数齐次线性微分方程,而式 (6)、(7)、(8)分别为
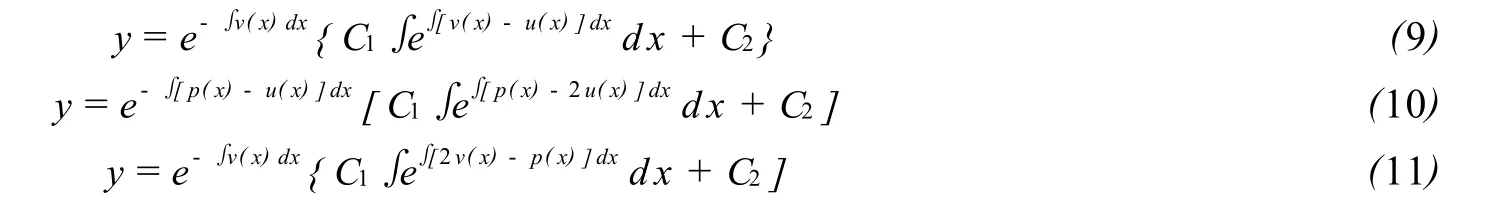
它们是对应的二阶变系数齐次线性微分方程的通解公式.
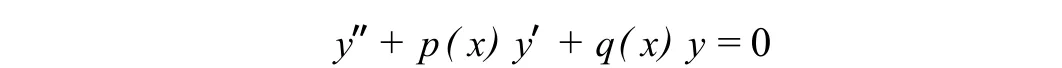
注意:以上的求解过程或方式就是二阶变系数线性微分方程的求解方法,公式 (6)、(7)、(8)均为二阶变系数非齐次线性微分方程 y″+p(x)y′+q(x)y=f(x)的通解公式.公式 (9)、(10)、(11)均为二阶变系数齐次线性微分方程 y″+p(x)y′+q(x)y=0的通解公式,在具体应用时,依据问题应灵活使用.
特别地2 形如
y″+[v(x)+u(x)]y′+[v′(x)+v(x)u(x)]y=f(x){C0n(y′)n+C1n(y′)n-1[p(x)y]+ …+Cnn[p(x)y]n}型的方程可化为伯努利方程.
原方程变形为
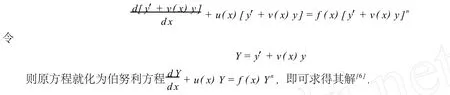
2 应 用
运用二阶变系数线性微分方程的一般求解法在求二阶变系数线性微分方程的解时,其重点是构造 (2)和 (3)式,难点或关键点是从 (2)式和 (3)式求出u(x)和v(x).或由 (2)式和 (3)式变形得
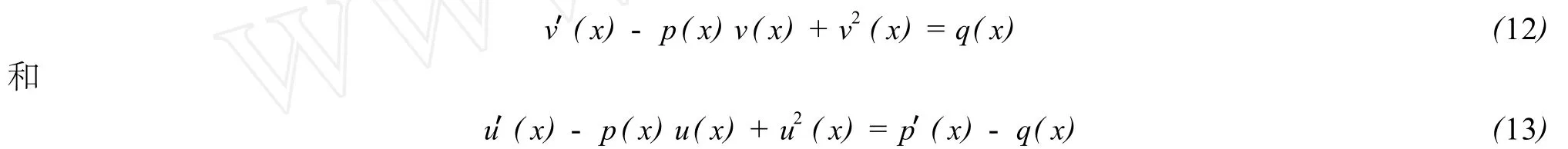
再从中求得u(x)和v(x).然后用上述方法或应用公式 (6)或 (7)或 (8)或公式 (9)或 (10)或(11)可求得二阶变系数线性微分方程的解.
注 方程 (12)或 (13)是黎卡提 (Riccati)方程,见《常微分方程》教材[7].
求二阶变系数线性微分方程解时,必须观察二阶变系数线性微分方程的特征.如果是上述特殊类型的二阶变系数线性微分方程,就用特殊类型的二阶变系数线性微分方程的求解方法求之;如果不是上述特殊类型的二阶变系数线性微分方程,就用二阶变系数线性微分方程的一般求解方法求之.
二阶变系数线性微分方程的一般求解步骤:
第一步:构造 (2)式和 (3)式
第二步:计算出u(x),v(x)
第三步:将第二步的结果代入上述公式求出通解来.
例 1 求 y″+[a+p(x)]y′+ap(x)y=0的通解
解 由方程特征可知 v(x) =a,u(x)=p(x),则

注意:对于常系数齐次线性微分方程的通解往往用特征根的方法求其通解.如果用以上降价法解常系数齐次线性微分方程的解更不成问题,但较特征根法烦琐一些.
例 2 求 y″+2y′+y=0的通解
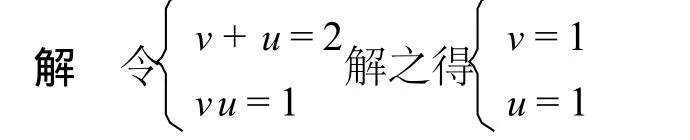
又知 p=2由以上公式,所求方程的通解为

特征根法:特征方程λ2+2λ+1=0有两个相等的实数根λ=-1.则所求方程的通解为y=e-x(c1x+c2)
[1] 同济大学应用数学系.高等数学 [M].北京:高等教育出版社,2003:259-317
[2] 王高雄.常微分方程 [M].北京:高等教育出版社,1985:101-163
[3] 李录苹,王通.关于几类二阶微分方-程的解法 [J].雁北师范学院学报,2006,22(02):71-72
[4] 李录苹.三阶变系数微分方程的三种可积类型 [J].山西大同大学学报,2008,24(01):16-18
[5] 龚东山,刘岳巍,贾筱景.计算一类常微分方程特解的新方法 [J].河北北方学院学报:自然科学版,2008,24(06):1-3
[6] 常秀芳,李高.伯努利方程的几种新解法 [J].雁北师范学院学报,2007,23(02):89-91
[7] 王高雄.常微分方程 [M].北京:高等教育出版社,1985:62
