覆盖空间中的庞开来对偶

李 彬，陈柏辉

(四川大学 数学学院，四川 成都 610064)

1 基础知识介绍

1.1 庞开来对偶

设X为n维可定向光滑紧流形,存在同构Hp(X;R)≅Hn-p(X;R),其中p∈Z,0≤p≤n.为方便起见，本文以下将采用Hp(X)，Hp(X)简记X上带R系数的上同调以及同调[1].

1.2 奇异同调与上同调的Pontrjagin对偶

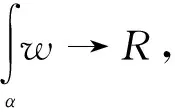
1.3 同调群中Pontrjagin对偶与庞开来对偶的交换性

1.4 正则覆盖定义

设X，Y为拓扑空间，称f:Y→X为正则覆盖映射，如果f为映上，并且∀x∈X，存在包含x的一个连通开集U，使得f-1(U)中任意一连通单元在映射f下分别同胚于U[4].

1.5 覆盖空间中的积分

设X，Y为n维可定向光滑紧流形，f:Y→X为正则覆盖映射，映射度为m，α为X空间中任意p维闭链，w为X空间中p阶微分形式，则[5]:

2 正则覆盖空间中庞开来对偶的性质

设X，Y为n维可定向光滑紧流形，f∶Y→X为正则覆盖映射，α为X空间中任意p维闭链，α∈Hp(X;R)，n-p维闭微分形式D(α)为其对应庞开来对偶，则f-1(α)与f*(D(α))为庞开来对偶.

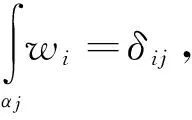
设D(α1)，D(α2)，…，D(αk)为α1，α2，…，αk对应n-p维庞开来对偶形式，由庞开来对偶相关性质可知:

从而

上式可诱导映射Φ:wi→D(αi)，从而建立Hp(X)，Hn-p(X)之间的同构Hp(X)≅Hn-p(X)

wi与D(αi)为庞开来对.

又由覆盖映射的积分性质:

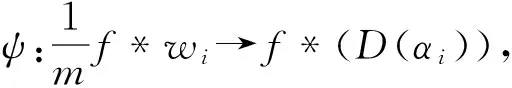
f*(Hp(Y))≅f*(Hn-p(Y))

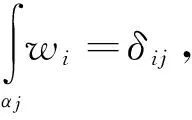
[1]J.R.曼克勒斯.代数拓扑基础[M].谢孔彬,译.北京:科学出版社,2006:473-480.

[2]苏竞存.流形的拓扑学[M].武汉:武汉大学出版社,2005:258-261.

[3]姜伯驹.同调论[M].北京:北京大学出版社,2006:212-215.

[4]李忠.复分析导引[M].北京:北京大学出版社,2004:143-151.

[5]Dubrovin,Fomenko,Novikov.Modern Geometry-Methods and Applications(part2)[M].Springer,1985：110-112.

[6]陈省身,陈维桓.微分几何讲义[M].北京:北京大学出版社，1983:1-321.

[7]William Fulton.Algebraic Topology[M].Springer,1995:1-430.