会议筹备的优化模型

程 丽，胡英武，李代华，余素娟，吴丹萍

(金华职业技术学院师范学院，浙江金华 321017)

会议筹备的优化模型

程 丽，胡英武，李代华，余素娟，吴丹萍

(金华职业技术学院师范学院，浙江金华 321017)

利用数学规划和概率统计知识对会议筹备问题进行了讨论，从经济、方便、代表满意等方面出发，建立了预定宾馆客房的0－1规划以及相应的线性规划。在一些合理的假设下，给出租借会议室、租用客车的方案，从而使租借会议室与租用客车的总费用尽可能少。最后，指出了模型中没有考虑进去的因素，并提出了模型的改进方向，以满足实际的要求。

会议筹备;0－1规划;穷举法

1 问题的提出

2009年，高教社杯全国大学生数学建模竞赛D题提出会议筹备问题。某会议服务公司负责承办一届全国性会议，会议筹备组要为与会代表预订宾馆客房，租借会议室，并租用客车接送代表。由于预计会议规模庞大，而适于接待这次会议的几家宾馆的客房和会议室数量均有限，所以只能让与会代表分散到若干家宾馆住宿。为了便于管理，除了尽量满足代表在价位等方面的需求之外，所选择的宾馆数量应该尽可能少，并且距离上比较靠近。再者，如果预订客房的数量大于实际用房数量，筹备组需要支付一天的空房费，而若出现预订客房数量不足，则将造成非常被动的局面，引起代表的不满。会议期间，有一天的上下午各安排6个分组会议，筹备组需要在代表下榻的某几个宾馆租借会议室。租借客车方面:由于事先无法知道哪些代表准备参加哪个分组会，筹备组需向汽车租赁公司租用客车接送代表，现有45座、36座和33座3种类型的客车，租金分别是半天800元、700元和600元。本文通过数学建模的方法，从经济、方便、代表满意等方面，为会议筹备组制定一个预订宾馆客房、租借会议室、租用客车的合理方案。

2 问题的假设

1) 车辆都靠边并沿直线行驶。

2) 6个 分组会议都同时召开，上午和下午安排的会议场地不变，参加的代表也不变。

3)上午6场会议的内容是相同的，下午6场会议的内容相同。

4) 当奇数个人去住双人间时当偶数个人去处理。

5) 一辆客车可以送代表去不同的目的地。

6) 每辆客车尽可能载满，一个宾馆没载满可到其他宾馆载满。

7) 考虑时间问题，避免代表迟到，每辆客车每半天只送两趟即客车在出发点只能出发两次。

3 符号说明

Pi:表示以往几届已到人数占发来回执人数的百分比。(i=1，2，3，4)

P:表示以往几届已到人数占发来回执人数百分比的平均值。

dij:表示第i个宾馆到第j个宾馆的客车行驶距离。(i、j=1，2，…，10)

u:租用45座客车的数量。

v:租用36座客车的数量。

w:租用33座客车的数量。

4 问题的分析和模型的建立与求解

4.1 利用概率知识求出本届会议可能参加代表的住房情况

根据D题附表3的以往几届会议代表回执和与会情况，求出以往几届会议已到人数占发来回执人数的百分比。

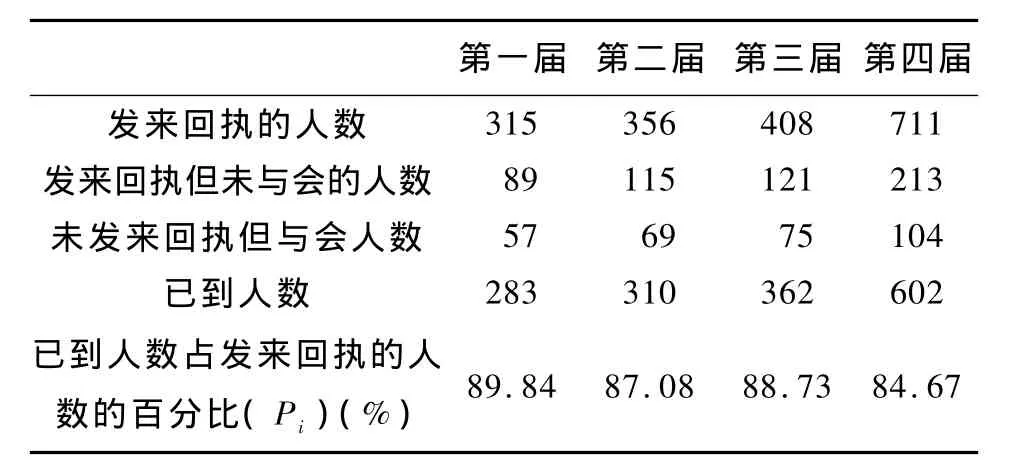
表1 以往几届已到人数占发来回执人数的百分比

87.58% 。从经济角度出发，为了使预订的客房不出现浪费或不足的局面，根据P值，对D题附表2的本届会议的代表回执中有关住房要求的信息做一定的处理，让它更符合实际。

表2 本届会议可能参加的代表住房要求的情况 人

由表2求出本届会议可能参加的人数为655人。再根据D题附表1的数据，对10个宾馆各个价位的房间数量进行统计得表3。

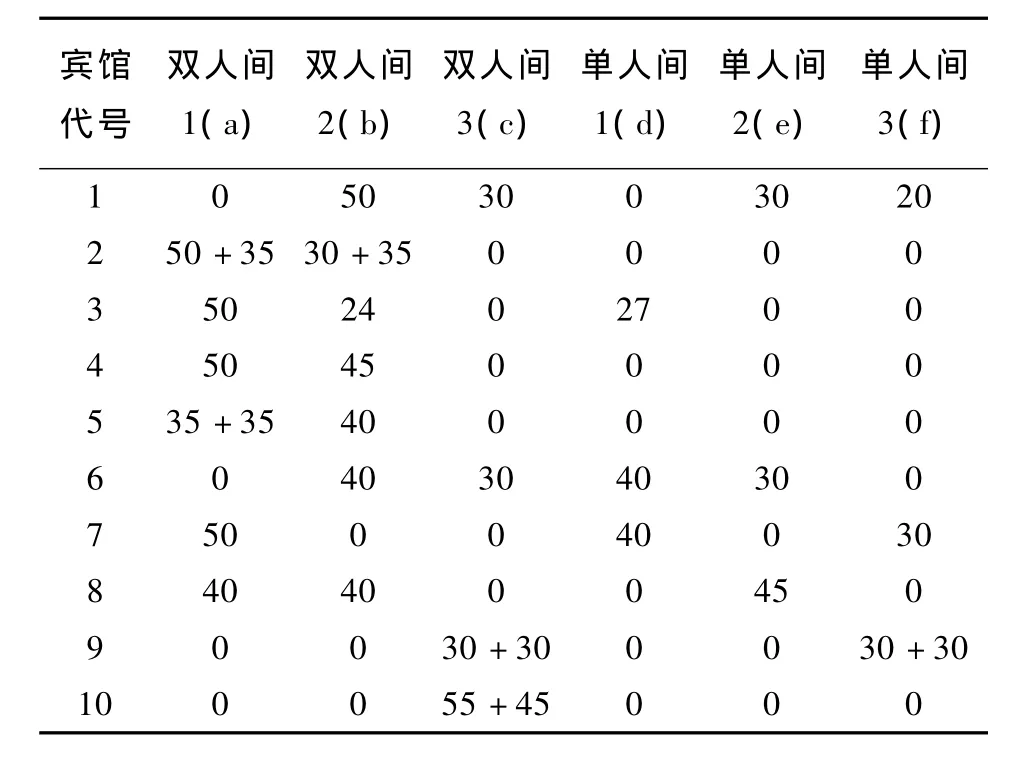
表3 10个宾馆各个价位的房间数量 间

4.2 建立选择宾馆的模型

为了便于管理，首先要满足所选的宾馆数量尽可能少的要求，因此，对于宾馆的房间，我们要充分地利用。在满足合住的要求下，在安排独住时，可以把独住的人安排单人间或让一个人单独住一个双人间。基于此原则，以宾馆数量尽可能少为目标，建立如下的0－1规划模型:xi=0或1(0表示不选择第i个宾馆，1表示选择第i个宾馆)。

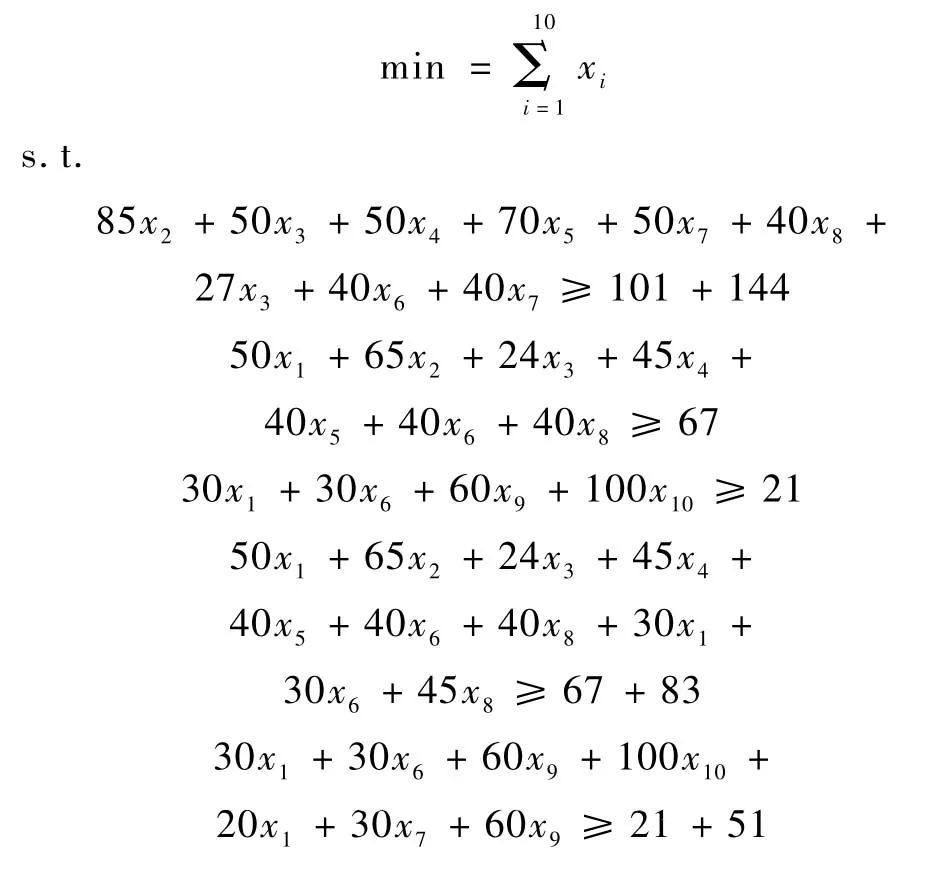
运用Lingo程序，求得有两种解:第一种x1=x2=x3=x7=1，其他为0;第二种 x1=x2=x5=x7=1，其他为0。

当 x1=x2=x3=x7=1，其他为0 时，xi=4，d11=d22=d33=d77=0，d12=150m，d23=750 m，d27=450 m，d13=900 m，d37=1 200 m，d17=300 m，比较得出:max dij=d37=1200 m。

当x1=x2=x5=x7=1，其他为0时，xi=4，d11=d22=d55=d77=0，d12=150 m，d15=600 m，d17=300 m，d25=750 m，d27=450 m，d57=300 m，比较得出:max dij=d25=750 m。

通过两种结果的比较，d37=1 200 m>750 m=d25，说明宾馆 1、2、5、7 距离上比较靠近，因此选择这4个宾馆安排代表。

4.3 建立已选择宾馆的客房预定模型

从经济、代表满意等方面出发，以住房总价格尽可能少为目标，为会议筹备组制定一个向1、2、5、7这4家宾馆预定客房的方案。设

x1b:表示宾馆1价格为180元/天普通双标间的预定间数。

x1c:表示宾馆1价格为220元/天商务双标间的预定间数。

x1e:表示宾馆1价格为180元/天普通单人间的预定间数。

x1f:表示宾馆1价格为220元/天商务单人间的预定间数。

x7a:表示宾馆7价格为150元/天普通双标间的预定间数。

x7d:表示宾馆7价格为160元/天商务单人间的预定间数。

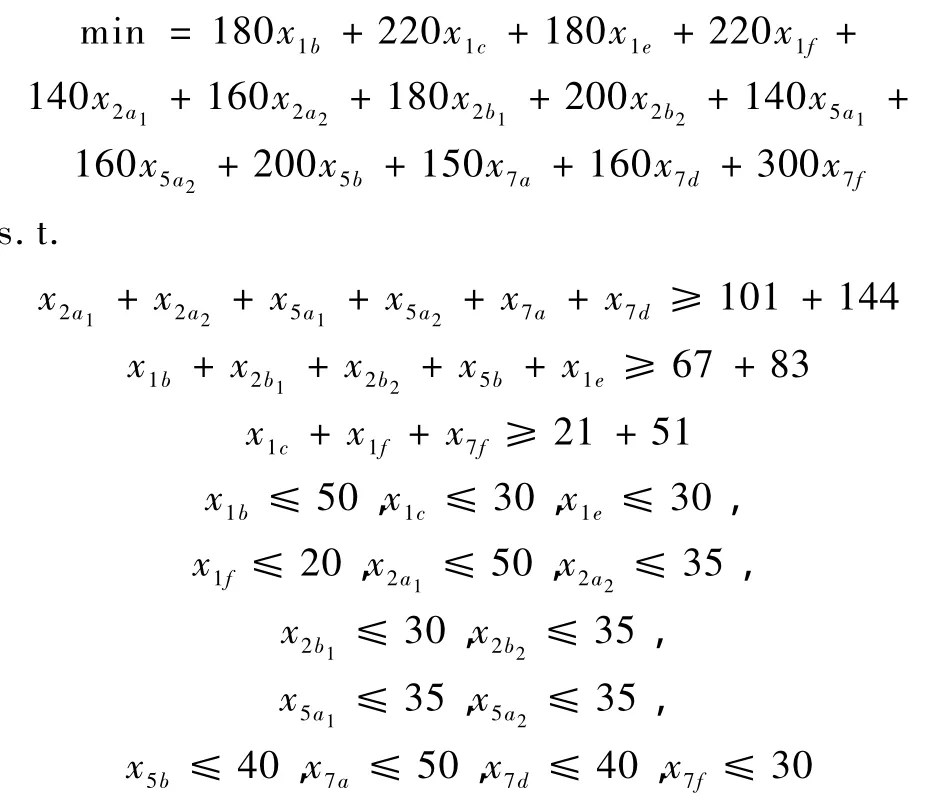
x7f:表示宾馆7价格为300元/天商务套房(1床)的预定间数。x1b，x1c，x1e，x1f，x2a1，x2a2，x2b1，x2b2，x5a1，x5a2，x5b，x7a，x7d，x7f为非负整数。

利用lingo程序解得最优值为82 400元，这时，x1b=50、x1c=30、x1e=30、x1f=20、x2a1=50、x2a2=35、x2b1=30、x2b2=0、x5a1=35、x5a2=35、x5b=40、x7a=50、x7d=40、x7f=22。

由于独住可安排单人间，或让一人单独住一个双人间。因此，双人间在先满足合住的前提下，余下的安排独住，具体分配见表4。

要求合住2的男代表出席人数为奇数，此多余的代表只能让他单独住双人间，不妨把他安排在宾馆1。从上表中可以求出，宾馆1居住的人数为178人，宾馆2居住的人数为174人，宾馆5居住的人数为166人，宾馆7居住的人数为137人。

4.4 制定租借会议室和租用客车的合理方案

会议期间，有一天的上下午各安排6个分组会议，由模型的假设，我们只考虑半天的安排。在预订宾馆的基础上，对分组会议人数的确定按以下两种情况进行讨论。

1) 会议人数以会议室规模为准

相比之下，租用客车的半天租金比租借会议室的半天费用要高很多，因此不租车应是最优安排。我们在1、2、5、7每个宾馆都租借会议室，在这个宾馆住的就在这个宾馆开会。设

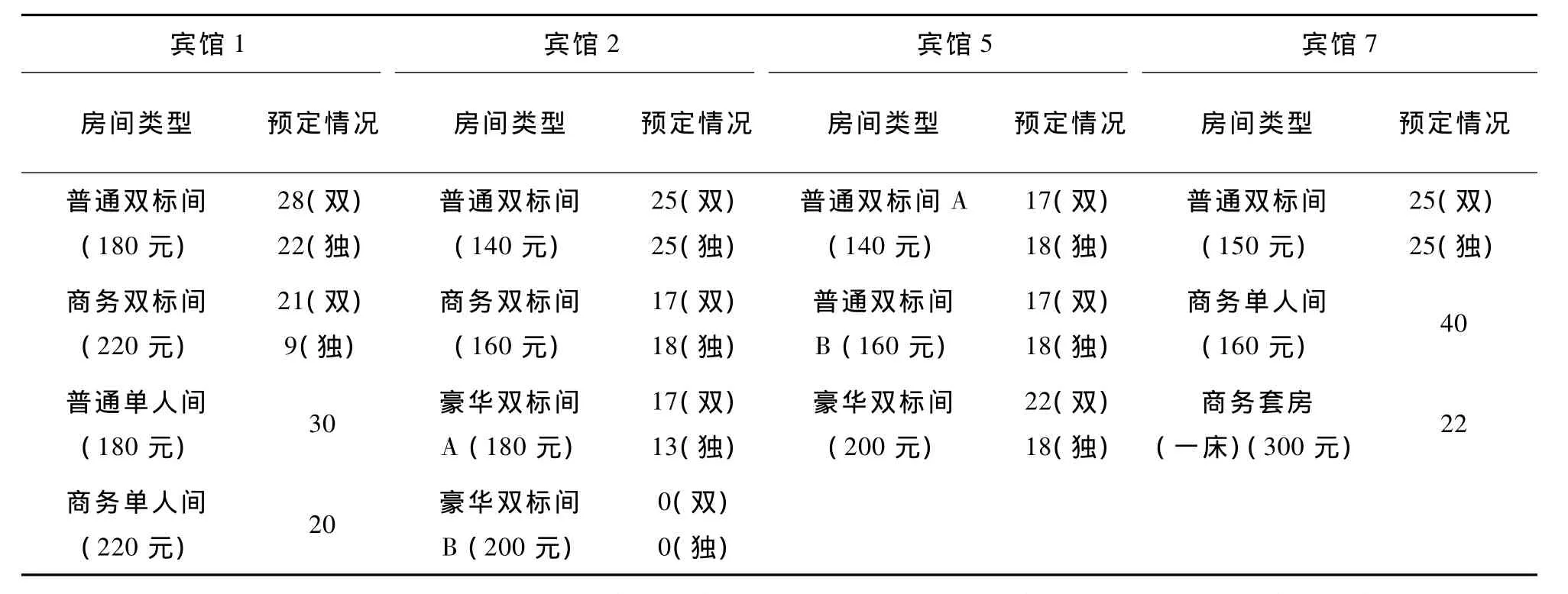
表4预定的宾馆客房分配情况

h11:表示宾馆1价格为1 500元/半天会议室的租借间数。

h12:表示宾馆1价格为1 200元/半天会议室的租借间数。

h13:表示宾馆1价格为600元/半天会议室的租借间数。

h21:表示宾馆2价格为1 000元/半天会议室的租借间数。

h22:表示宾馆2价格为1 500元/半天会议室的租借间数。

h23:表示宾馆2价格为300元/半天并容纳45人的会议室的租借间数。

h24:表示宾馆2价格为300元/半天并容纳30人的会议室租借的间数。

h51:表示宾馆5价格为1 000元/半天会议室的租借间数。

h52:表示宾馆5价格为1 500元/半天会议室的租借间数。

h53:表示宾馆5价格为500元/半天会议室的租借间数。

h71:表示宾馆7价格为800元/半天会议室的租借间数。

h72:表示宾馆7价格为300元/半天会议室的租借间数。

h73:表示宾馆7价格为1 000元/半天会议室的租借间数。

以租借会议室半天的总费用最少为目标，可得整数规划:

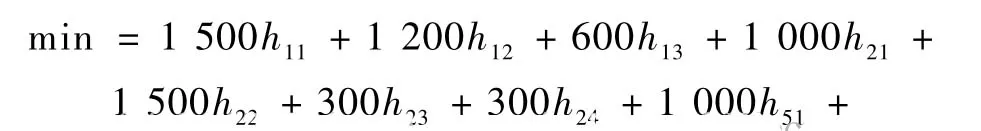
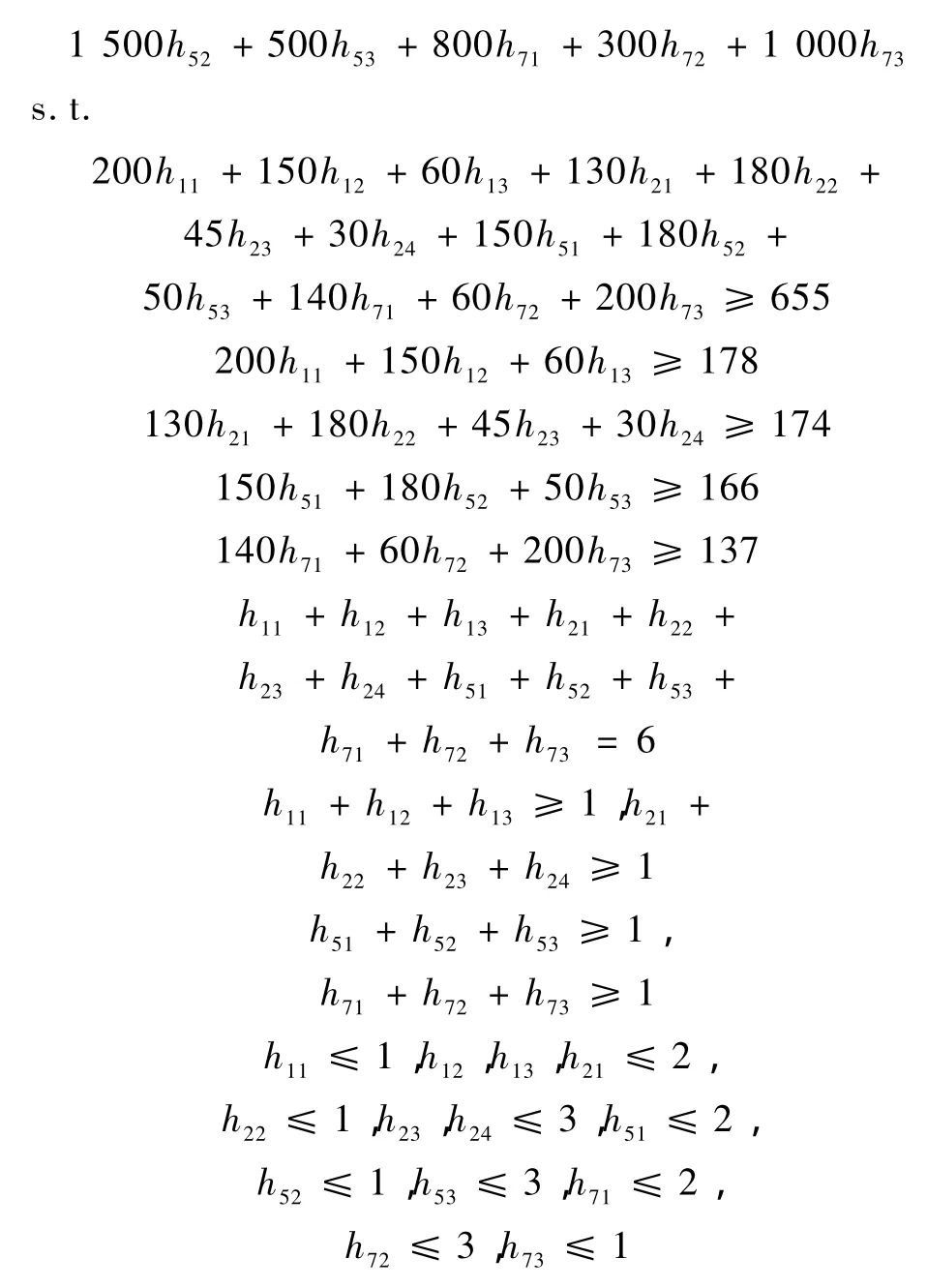
h11，h12，h13，h21，h22，h23，h24，h51，h52，h53，h71，h72，h73为非负整数。

解得 h11=h21=h23=h51=h53=h71=1，其余为0，即在宾馆1租借一个价格1 500元/半天的会议室，在宾馆2租借一个价格1 000元/半天的会议室、一个价格300元/半天并容纳45人的会议室，在宾馆5租借一个价格1 000元/半天的会议室和一个价格500元/半天的会议室，在宾馆7租借一个价格800元/半天的会议室，此时不需要租车。半天租借会议室的总费用为5 100元，一天为10 200元。

2)会议人数平均分配

根据本届会议可能参加的人数为655人，计算出每个分组会议的人数大约为 109人，即每个会议室的规模应大于109人。若还是在1、2、5、7每个宾馆都租借会议室，则必定有一个宾馆将租借2个会议室，这样到此宾馆开会的大约有220人，而这4个宾馆居住的人数都不超过180人，因此筹备组必须要租用客车接送代表。

虽然租用客车的租金是以半天计算，但是考虑时间问题，为了避免代表迟到，假设每辆客车每半天只送两趟，并尽量让客车坐满，一个宾馆没载满可到其他宾馆载满，一趟可以送代表去不同的目的地。

如果6个会议室分别租借在4个宾馆，则有2个宾馆要租2个会议室或有1个宾馆要租3个会议室，用排列组合算出共有10种情况。

以宾馆1、2各租两个会议室，宾馆5、7各租一个会议室为例，建立模型:

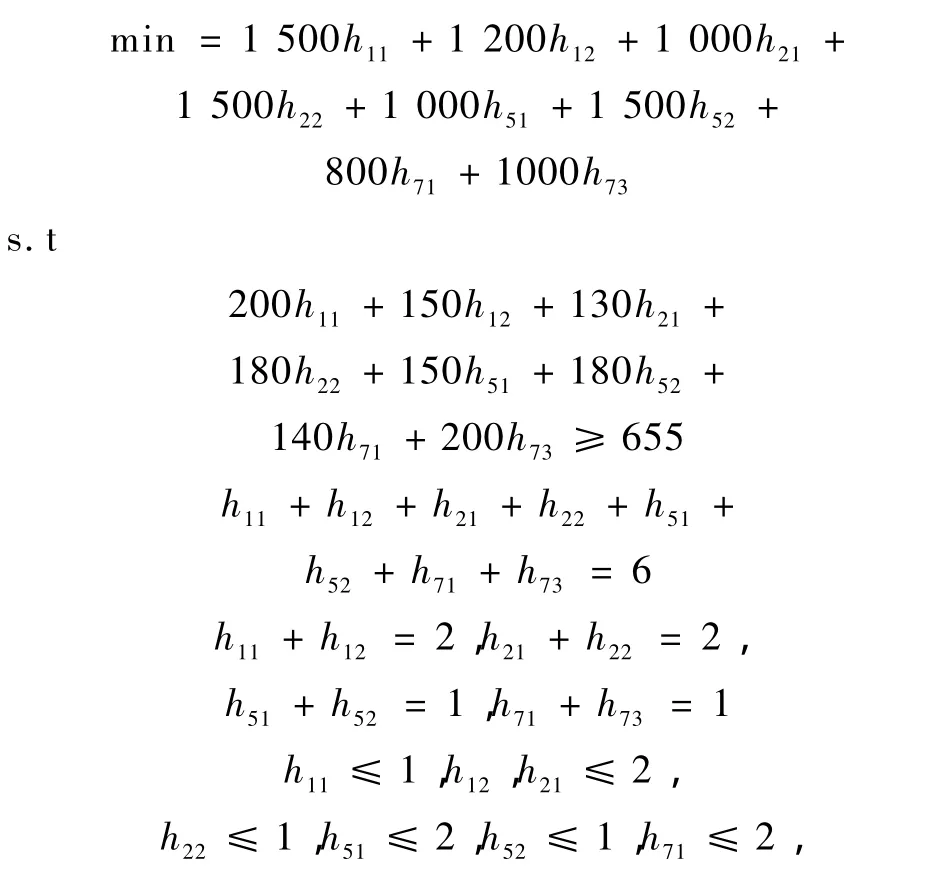
h73≤1，h11，h12，h21，h22，h51，h52，h71，h73为非负整数。

得 h12=h21=2，h51=h71=1，其余为 0，目标函数最优解为6 200元。但在宾馆5租借了一个会议室，须把166－109=57人送到宾馆1或2参加会议，同样也须把宾馆7的137－109=28人送到宾馆1或2参加会议，于是又建立如下模型:

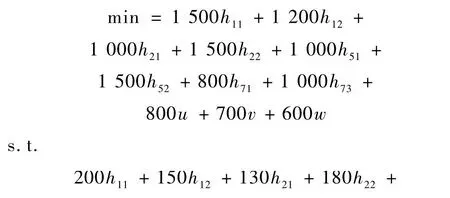
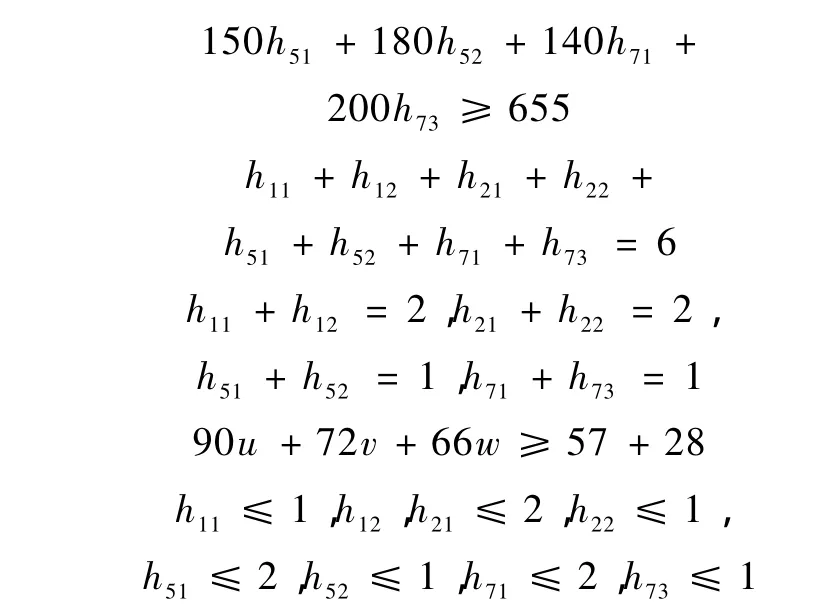
h11，h12，h21，h22，h51，h52，h71，h73为非负整数。

得 h12=h21=2，h51=h71=1，u=1，其余为 0，目标函数最优解为7 000元。

其余9种情况同样建立规划可得，其计算结果见表5。

如果6个会议室租借在3个宾馆，则有4种情况，对于每一种情况，先不考虑要送的代表人数，求出租用会议室的最少费用，然后再考虑至少要送的代表，求出租借会议室和租用客车至少所需的总费用，见表6。

如果6个会议室租借在两个宾馆，则至少有137+166=303位代表要送，租用客车至少需u=2辆，w=2辆，即需租金2 800元，而不考虑任何限制，租6个规模大于109人会议室最优地点是h21=h51=h71=2，租金为5 600元，这样半天总费用至少要8 400元。

如果6个会议室都租借在同一个宾馆里，这是不能安排的。

综上所述，要使总费用最少，应在宾馆1中租借两个价格为1 200元/半天的会议室，在宾馆2租借两个价格为1 000元/半天的会议室，在宾馆5租借一个价格为1 000元/半天的会议室，在宾馆7租借一个价格为800元/半天的会议室，并租用45座类型的客车一辆;或在宾馆1租借选择一个价格为1 200元/半天的会议室，在宾馆2租借两个价格为1 000元/半天的会议室，在宾馆5租借一个价格为1 000元/半天的会议室，在宾馆7租借两个价格为800元/半天的会议室，并租用33座类型的客车两辆，此时半天总费用都为7 000元，一天就为14 000元。

5 模型分析与改进

论文就会议筹备优化模型进行分析讨论。在尽可能提高与会代表对住房满意度的前提下来讨论预定宾馆客房的方案，计算出居住在宾馆1、2、5、7各自的总人数;对于分组会议人数的不同情形，利用穷举法列举出各种会议室分布情况，进而求出租借会议室和客车的最省总费用。

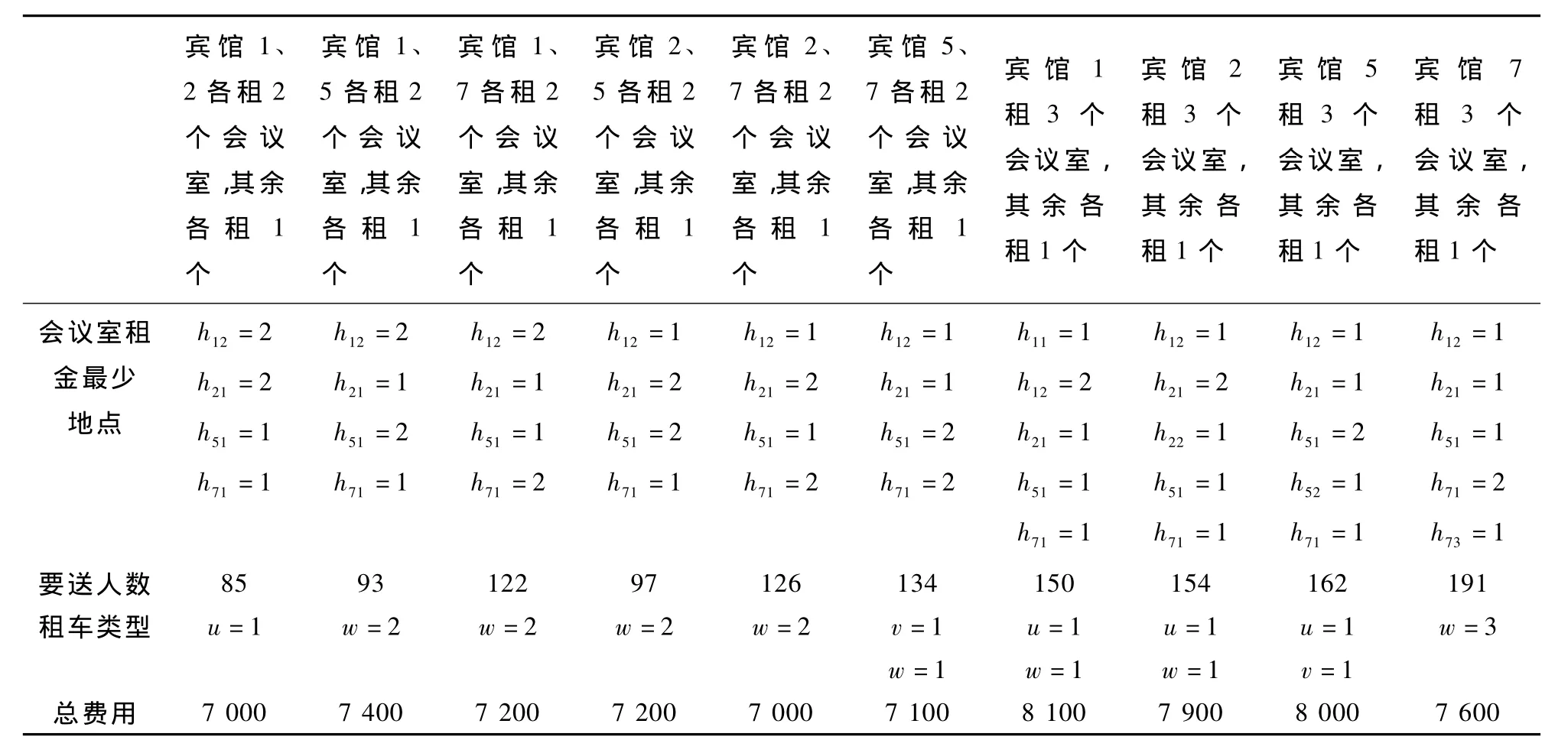
表5 在4个宾馆都租借会议室以及客车租用的情况

表6 在3个宾馆租借会议室以及客车租用的情况

在选择会议室的时候，我们的模型还存在一些不足之处，即本文假设6个分组会议的内容是相同的，没有考虑6个分组会议的内容互不相同，代表需到指定的会议室这一变因;在安排客车接送代表时，也只考虑每辆客车每半天只送两趟，没有考虑客车接送次数变化，而这些因素很可能会对模型的稳定性产生影响，不利于模型的推广，模型有待于进一步地改进与优化。但无论如何，我们所建的模型对筹划组的工作人员还是有一定的实际指导意义的。

［1］ 姜启源.数学模型［M］.北京:高等教育出版社，2003.

［2］ 袁新生.Lingo和Excel在数学建模中的应用［M］.北京:科学出版社，2007.

［3］ 叶其孝.大学生数学建模竞赛辅导材料(三)［M］.长沙:湖南教育出版社，1999.

［4］ 袁荫棠.概率论与数理统计［M］.北京:中国人民大学出版社，2000.

［5］ 吴建国.数学建模案例精编［M］.北京:中国水利水电出版社，2005.

An Optimality Model of Conference Preparations

CHENG Li，HU Ying-wu，LI Dai-hua，YV Su-juan，WU Dan-ping

(Normal school of Jinhua College of Profession and Technology，Jinhua Zhejiang 321017，China)

An optimality model of conference preparations was discussed on the theory of mathematical programming and probability.First，some mathematical programming problems about hotels chosen and guestroom reservation were given from the perspectives of economy，convenience，and satisfaction of participants.Second，a reasonable plan for the Local Organizing Committee in their meeting room lease and coach lease by use of mathematical modeling is made under some reasonable hypothesis.Some fault and improvement about the model are pointed out in the end.

conference preparations;0－1 programming problem;exhaustive method

O 141.4

A

1005-0310(2010)01-0067-06

2009－10－08

程丽(1972—)女，浙江永康人，金华职业技术学院副教授，硕士，研究方向为最优化理论。

(责任编辑 李亚青)