楼层间含有大质量结构的动力特性分析

金丽萍

(中冶华天工程技术有限公司,安徽马鞍山 243005)

楼层间含有大质量结构的动力特性分析

金丽萍

(中冶华天工程技术有限公司,安徽马鞍山 243005)

用有限元分析软件SAP2000对楼层间存在大质量结构的动力特性进行了分析,通过不同简化设计方法的对比,给出了此类结构行之有效的简化设计方法,供工程设计参考。

楼层间大质量结构; 动力特性; 地震响应

在许多工业建筑中为了满足工艺需要,常常需要在楼层间设置一些质量比较大的设备或原料仓(例如冶金工厂的喷煤厂房就需要在楼层间设置原煤仓和煤粉仓),由于这些设备或原料仓的存在致使这一类结构在楼层间存在大质量。目前对楼层间存在大质量结构的设计方法一般是将楼层间的质量转化为活荷载或恒荷载施加于质量所在的楼层,然后按照楼层间不存在大质量的普通结构进行设计。这一解决方法,是否与结构实际情况接近,其精度能否满足工程需要,目前尚未看到关于此方面的文献。本文通过有限元分析对楼层间存在大质量结构的动力特性进行了研究,并对将质量转化为荷载的设计方法的精度进行了分析,得出了一些有意义的结论,供设计参考。

1 计算模型建立

为了研究楼层间存在大质量结构,本文设计了三组试件即 SJ1～SJ3。试件为六层工业建筑,在第 2、6层分别设有原料仓,从SJ1～SJ3仓重分别为200 t、400 t、600 t。为了进行对比每组试件包括:(1)料仓满仓(以下称:满仓);(2)料仓空仓(以下称:空仓);(3)将料仓满仓时质量转化为活荷载作用于楼层(以下称:活载);(4)将料仓满仓时质量转化为恒载作用于楼层(以下称:恒载),四个试件。为了研究不同仓重对结构的影响,六组试件柱距均为 10m,层高均为 6m,梁、板、柱的截面尺寸均相同。试件材料为钢筋混凝土。

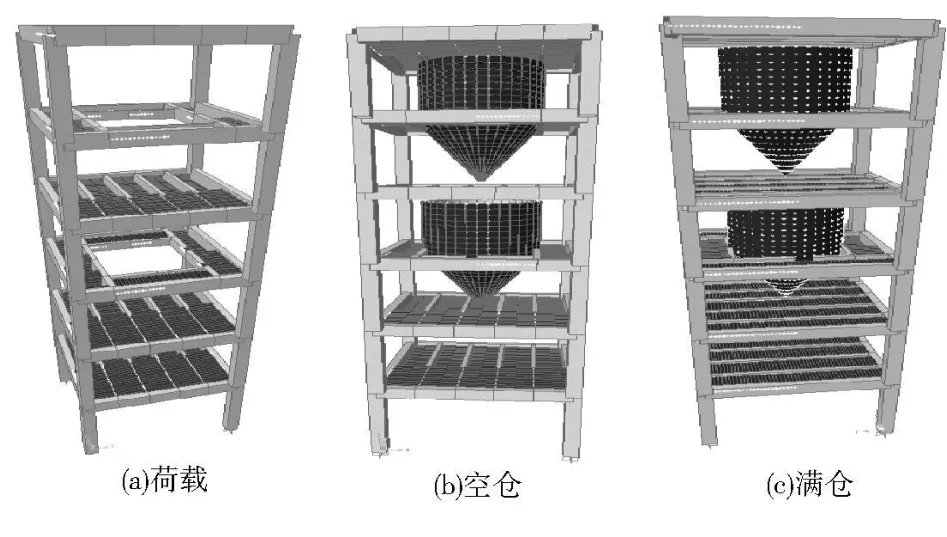
图1 三维模型图

试件分析采用有限元分析软件SAP 2000进行,分析时梁、柱用框架单元模拟,楼板用壳单元模拟,料仓空仓时仓壁用壳单元模拟,满仓时将仓料与仓壁考虑为同一种材料用实体单元模拟,所有仓的外形尺寸均相同,通过改变材料密度达到不同仓重的目的。为了接近实际情况分析时除了仓重外在每层楼面施加了 5 kN/m2的活荷载。图 1为试件三维模型图。

图2 SJ2第一振型

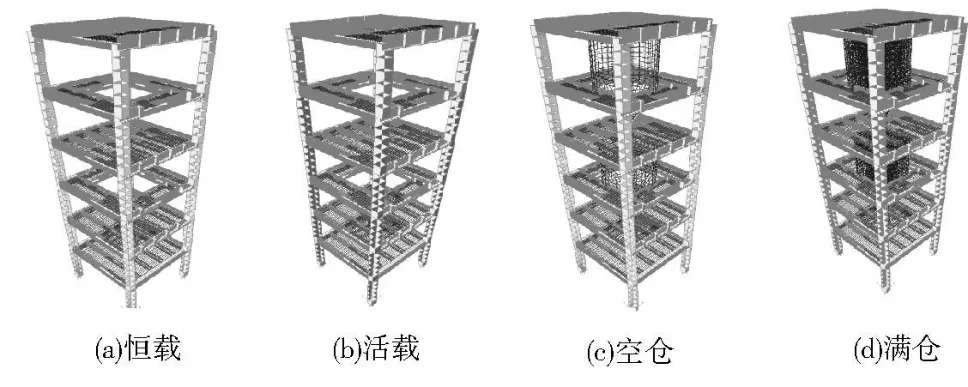
图3 SJ2第二振型

图4 SJ2第三振型

2 动力特性分析

《建筑抗震设计规范》规定“不进行扭转偶联计算的结构计算地震作用效应时可只取前 2～3个振型”,试件SJ2的前 3阶振型见图 2～图 4。

从图 2～图 4可以看出,结构的前三阶阵型分别为沿 X和 Y方向的平动和扭转振动。无论是空仓时还是满仓时或者是将仓体质量转化为荷载作用于楼层,结构的阵型形状比较接近,这是因为本文所选的结构体系比较简单,无论何种情况结构的质量集中点变化不大,因此结构的阵型比较接近。

表 1～表3为各组试件前 10阶阵型的自振周期。图5～图 7为各组试件前十阶阵型周期变化趋势。从表 1～表 3和图 5～图 7可以看出由于料仓空仓和满仓时楼层间质量变化较大,空仓和满仓两种状态的自振周期变化较大,并且随着仓重的增加两种状态下的自振周期差距越来越大。自振周期的不同将直接导致结构地震响应的不同,设计此类结构时应分满仓和空仓两个状态分别计算自振周期及地震响应,取不利情况进行设计。

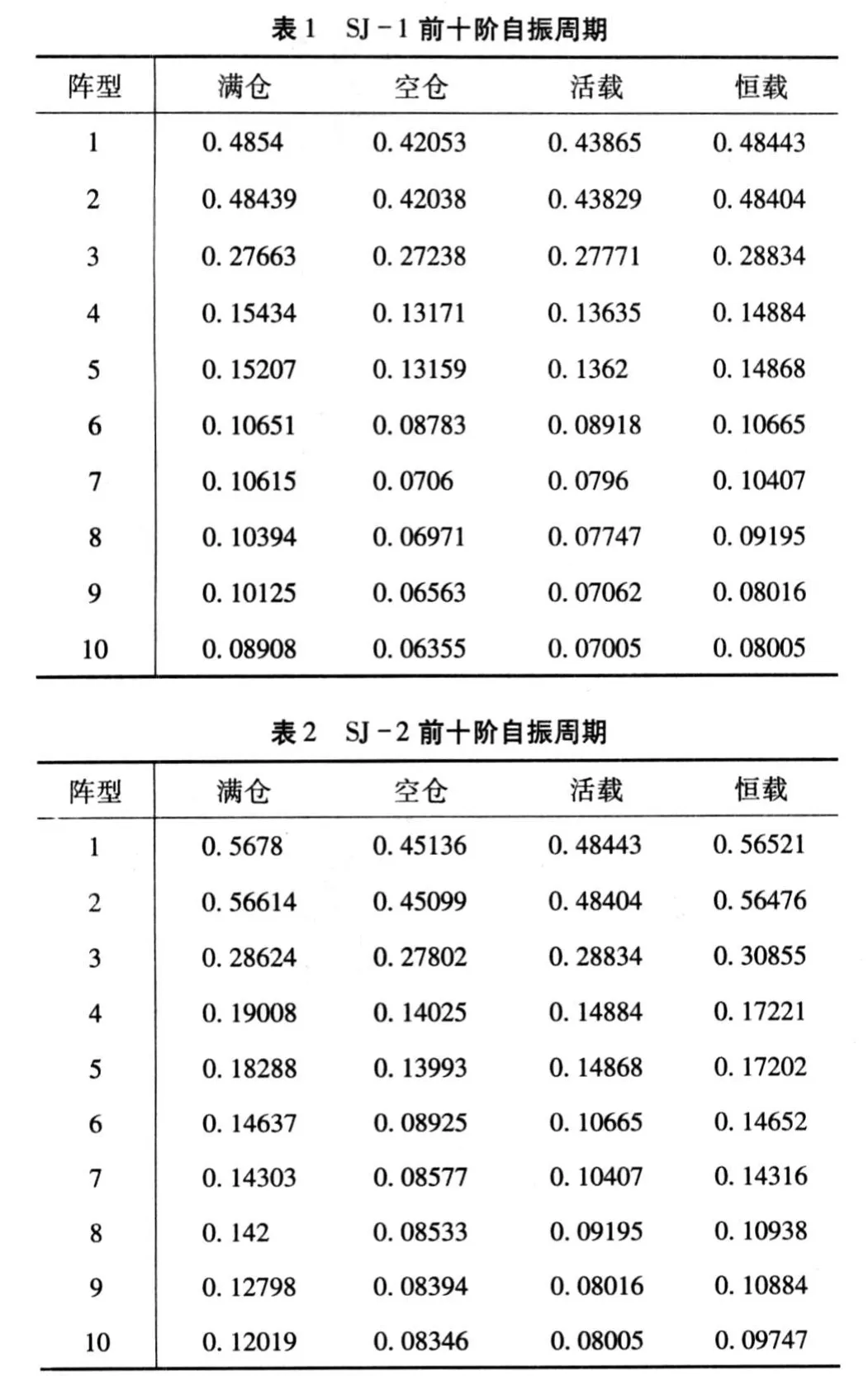
图5 SJ-1周期变化趋势

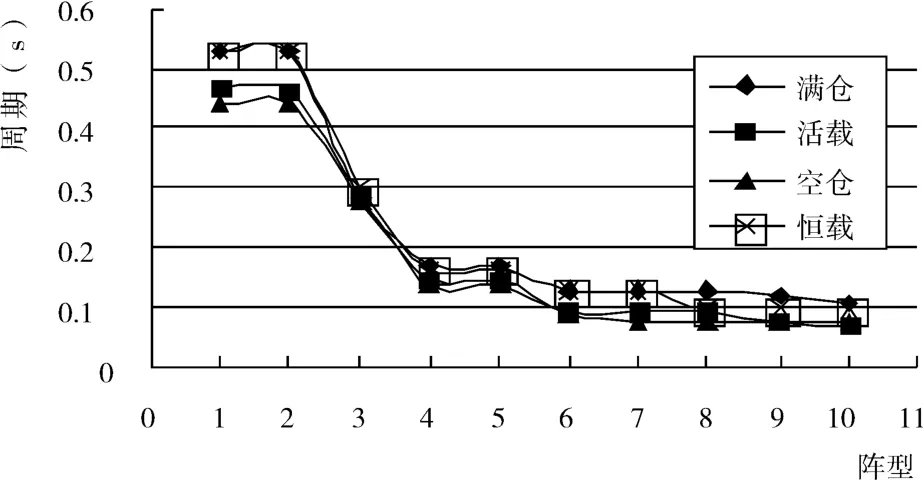
图6 SJ-2周期变化趋势

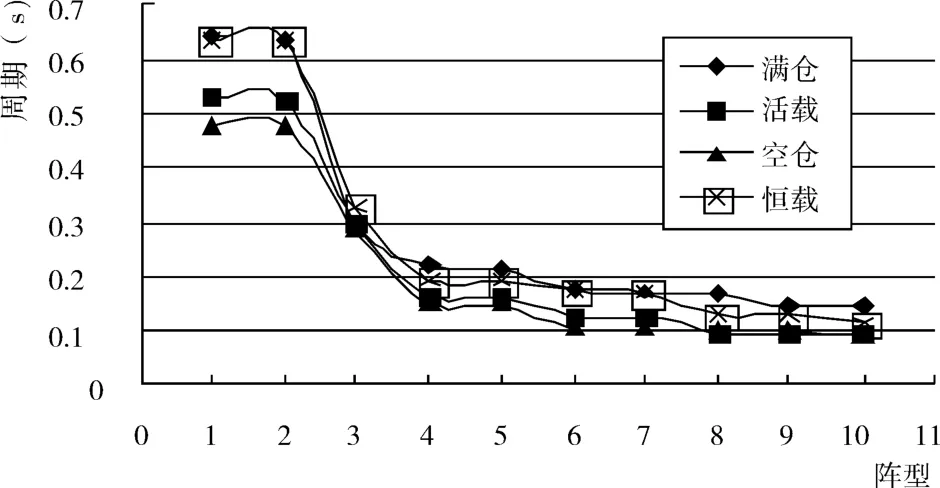
图7 SJ-3周期变化趋势

将满仓质量转化为恒载和活载分别作用在楼层表面的简化方法由于程序计算时对恒载和活载对质量贡献的不同取值,导致两种简化方法的周期差异。两种简化方法各阵型周期始终位于满仓和空仓两种状态周期之间,并且转化为恒载简化方法的各阶周期与满仓状态的周期十分接近,分析此类结构时可以以此种方法计算的周期代替满仓状态下的周期。转化为活载简化方法的各阶周期与空仓状态周期比较接近,但仍有一定差距,对于空仓状态下的自振周期其简化计算可以采取与满仓状态相同的方法,将空仓时仓重的质量转化为恒载作用于楼层。经过以上简化计算方法,不但可以解决用程序计算时要建立仓的不便,还可以获得与实际情况十分接近的自振周期。

3 地震作用响应分析

楼层间存在大质量结构的周期在满仓和空仓状态下以及不同的简化计算方式下存在差异,自振周期的不同必将导致结构地震响应的不同。为了考察结构在不同状态下的地震响应,本文采用阵型分解反应谱法对结构X、Y方向的地震响应进行了分析。分析时设防烈度为 8度,场地类别为Ⅱ类,设计地震分组为第二组,阻尼比为0.05。

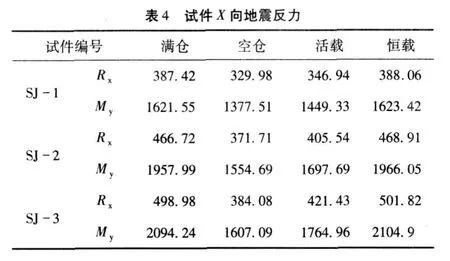
由于本文所分析试件X和Y方向为对称结构,两个方向的地震响应比较接近,因此只给出结构在X向地震作用下的柱底反力(见表 4)。从表 4可以看出,由于满仓和空仓两种状态下结构楼层间质量变化较大,致使空仓与满仓状态下结构地震反力存在较大差异,差距最大的SJ-3空仓时地震反力仅为满仓时的 77%左右,因此对于此类结构除了结构在空仓时周期接近场地特征周期,满仓时周期与场地特征周期相差较远的特殊情况下,空仓时地震反力有可能大于满仓时外,一般情况下空仓时地震反力均小于满仓时,进行结构设计时可只考虑满仓状态而不必考虑空仓状态下的地震反力。

从表 4可以看出将满仓时质量转化为活荷载作用在楼层的简化方法,计算的地震反力较满仓时的实际地震反力要小,并且随着仓重的增加差距越来越大。本文SJ-3中转化为活荷载的地震反力仅为满仓时实际地震反力的 84%,因此如果将此地震反力用于工程设计会不安全。将满仓时质量转化为恒荷载作用于楼层的简化方法算得的地震反力与满仓时实际地震反力几乎没什么差别,且其值稍微大于实际值,若将此值用于结构设计不但十分接近实际情况还偏于安全。对此类结构进行设计时可以采用将满仓质量转化为恒载的简化方法,此简化方法,不但便于实现,而且其简化结果与实际情况十分接近,是一种行之有效的方法。

4 结束语

楼层间存在大质量结构在满仓和空仓状态下结构自振周期存在较大差异,分析此类结构动力特性时应分空仓和满仓两种状态分别计算。分析楼层间存在大质量结构时可以将楼层间质量转化为恒荷载作用于楼层,然后按普通结构进行计算,此种简化方法计算所得结构自振周期、阵型、地震响应与结构实际周期、阵型、地震响应十分接近,操作简便且满足工程设计要求。

[1] GB 50011-2001建筑抗震设计规范[S]

[2] 张政,丁洁民,王忠平,等.双塔连体复杂高层结构的超限分析及抗震性能评价[J].建筑结构,2008,38(9):52-57

[3] 段振亚,谭蔚,聂清德,等.框架塔动力特性的有限单元法研究[J].化工机械,2004,31(5):272-275

TU312+.1

A

2010-02-24

金丽萍(1982～),女,满族,学士,从事结构设计和研究工作。