多跨短肢剪力墙的自由振动分析
2010-01-15李创第陈运凯陆运军
李创第,陈运凯,陆运军
(广西工学院,广西柳州 545006)
多跨短肢剪力墙的自由振动分析
李创第,陈运凯,陆运军
(广西工学院,广西柳州 545006)
针对多跨短肢剪力墙的自由振动进行研究。以多跨短肢剪力墙各跨连梁切口处位移为零建立包含水平位移和剪力流的微分方程,并将这些方程叠加起来,再根据剪力墙的弯矩-曲率关系式建立水平位移和外荷载弯矩四阶微分方程,根据达朗贝尔原理将该方程化为只含有水平位移的六阶微分方程。通过两端的边界条件,令其所组成的系数行列式为零,用试算法求出多跨短肢剪力墙的自振周期,进而得其振型图像。考虑了多跨短肢剪力墙中连梁的作用,从而得到了一个比较精确的解。
自由振动分析; 多跨短肢剪力墙; 自振周期
短肢剪力墙结构具有受力均匀,抗震性能好的优点,地震区建造此类结构是可行的[2]。由于关于短肢剪力墙的理论分析还不多,短肢剪力墙自振周期的研究更少,传统解析法求剪力墙结构自振周期的求法是以简单欧拉梁的模型建立自由振动方程,再根据边界条件得出方程的系数行列式不为零的条件求出自振周期。这种方法简单实用。然而欧拉梁模型所忽略的剪力墙结构中的连梁的作用,在短肢剪力墙结构连梁计算中却非常重要,简单的欧拉梁模型求出的自振周期将造成很大误差。因此建立一个考虑连梁作用的剪力墙模型来求短肢剪力墙的自振周期是非常有必要的。
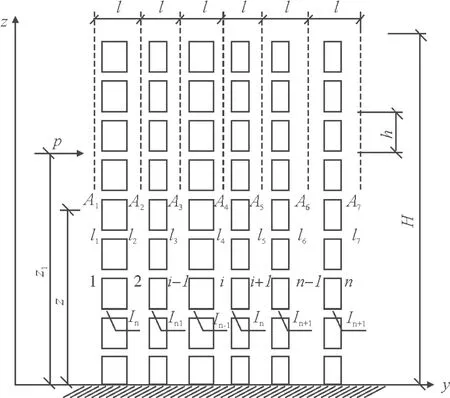
图1 带有n个墙肢的短肢剪力墙立面
1 自由振动微分方程
考虑如图1所示的多跨短肢剪力墙。层高为h,设墙肢i的横截面面积、惯性矩分别为Ai,Ii;第i列连梁的跨度为bi,横截面惯性矩为Ibi(i=1,2……n)。沿连系梁切口处在外荷载、切口处的轴向力和剪力共同作用下的相对位移为零。此相对位移由以下几部分组成[3]。
(1)由墙肢弯曲所引起的相对竖向位移:

式中:dy/dz为墙肢在高度Z处转角;li为第i跨洞口两侧墙肢轴线之间的距离。
(2)由连梁弯曲所引起的相对竖向位移:

式中:qi(z)为第i个连梁沿墙肢高度分布的剪力流。
(3)由于墙肢轴向力所引起的相对竖向位移:

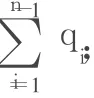
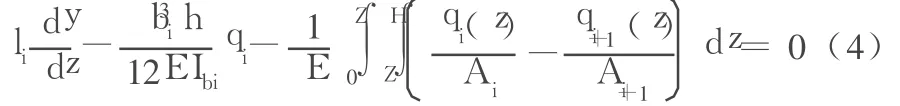
引入假定qi=ηiQ。这里,Q= ;ηi为连梁的总剪力在第 i列连梁中的分配系数。通过对连梁的变形以及与其相应的弯矩和剪力的分析,可以导出[4]
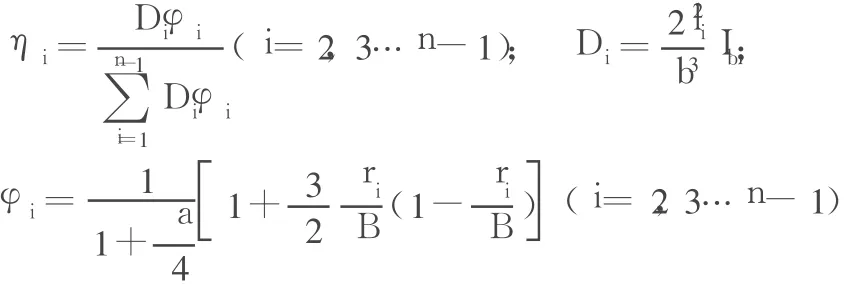
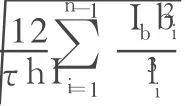
由式(4),依次令(i=2,3…n-1),并求和,则有:

在任意高度 z,外加水平荷载引起的弯矩为 M和剪力墙的曲率之间关系式为[3]:
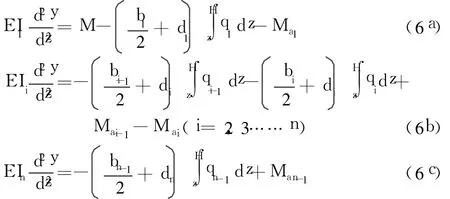
式中:di(i=1,2……n)为第i堵墙1/2截面高度; Man-1(i=1,2…n-1)为连梁的轴向力在墙肢中引起的弯矩。需要指出的是,连梁的轴向力总是成对出现,且每对轴向力的大小相等、方向相反,它们在按照如下方法求解时对问题的解答没有任何影响。
类似地,由式(6a)~式(6c)依次求和得:

式中:m为墙体单位高度质量。
把式(9)代入式(8),并将其对z求两次微分,得:
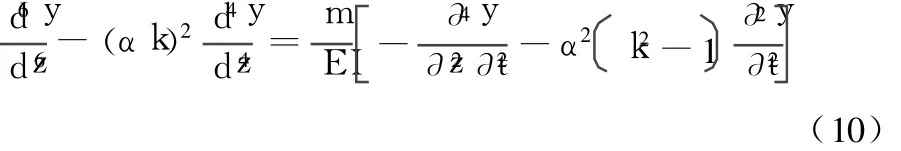

式中:Z=z/H;λ4=mω2/(EI)。
式(13)表示自由振动的状态方程。如果连肢墙是建在刚性基础上,则在连续系统中,无论 t取何值,其底部挠度、转角和分布剪力均为零。在自由端,无论 t取何值,每堵墙的弯矩、轴力和剪力也都为零。因此,式(13)的边界条件可归纳为如下的无量刚形式。
在底部(即Z=0,t为任意值):

2 自由振动方程的求解
式(13)为用无量刚形式描述的短肢剪力墙的自由振动方程,其通解[5]可表示为以下形式:
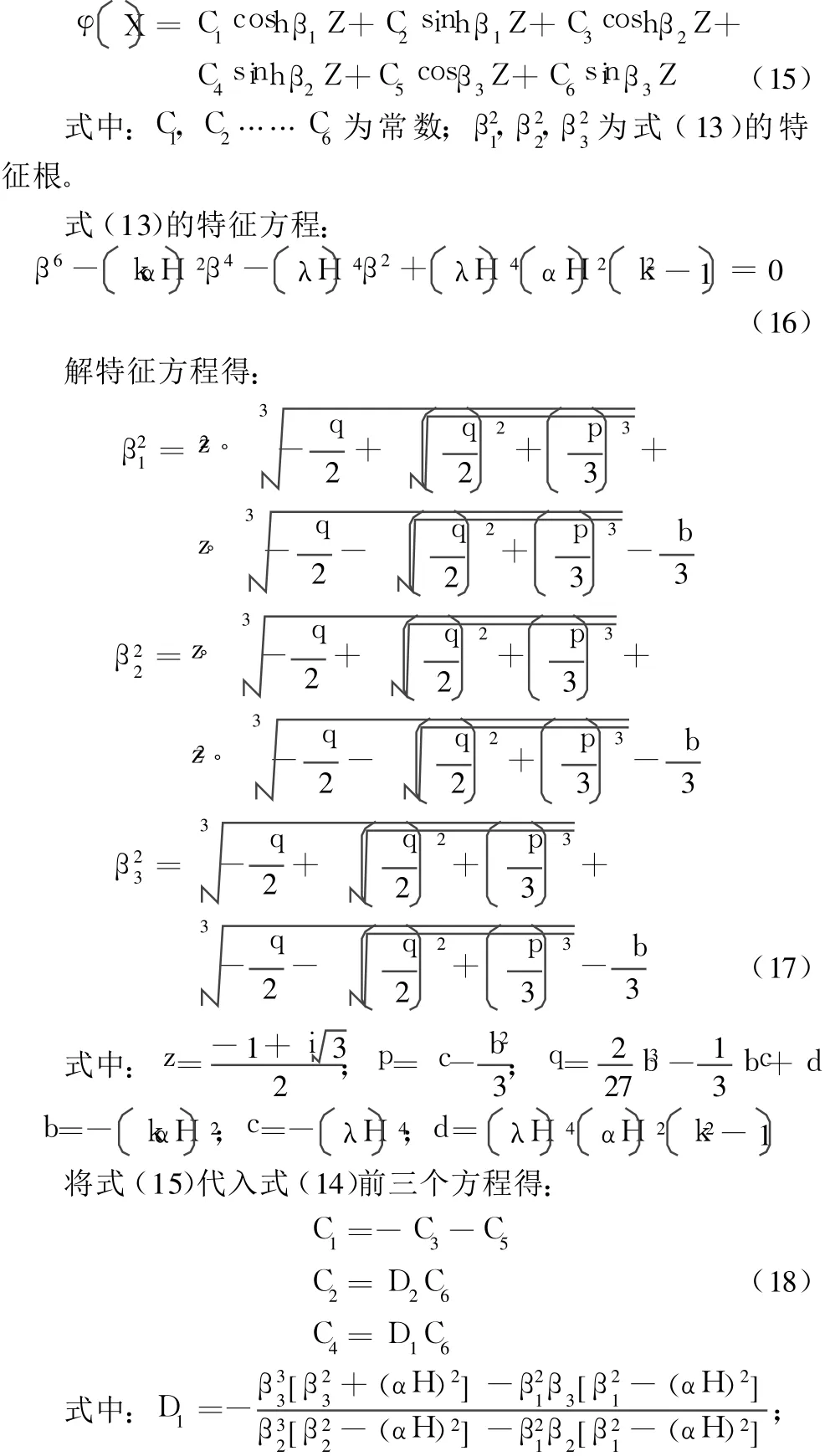
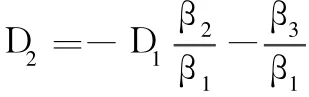
将式(15)代入式(14)的后三个方程,并利用式(18)的关系式得关于 C3,C5,C6的三个齐次方程组。并得到关于C3,C5,C6的系数矩阵;

3 算 例
某 26层短肢剪力墙结构建筑,该建筑由六堵四肢墙组成,如图 2所示。剪力墙各参数为:四墙肢截面高度均为 di=7.32m,层高h=2.74m,各连梁截面高度hbi=0.2m各连梁净跨bi=1.68m,沿高度质量分布m=653×103t/m,弹性模量E=25×106kN/m2,各墙横截面积Ai=13.4 m2,各墙惯性矩Ii=59.7m4,连梁惯性矩Ibi=0.0064m4。
代入公式计算得l1=l2=l3=9 m;I=238.8 m4;a= 0.12;φ1=φ2=φ3=1
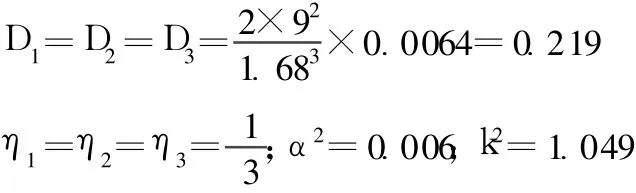
编入MATLAB程序利用试值法进行计算,前三阶振型周期的结果见表 1。
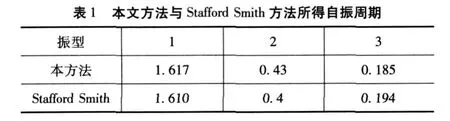
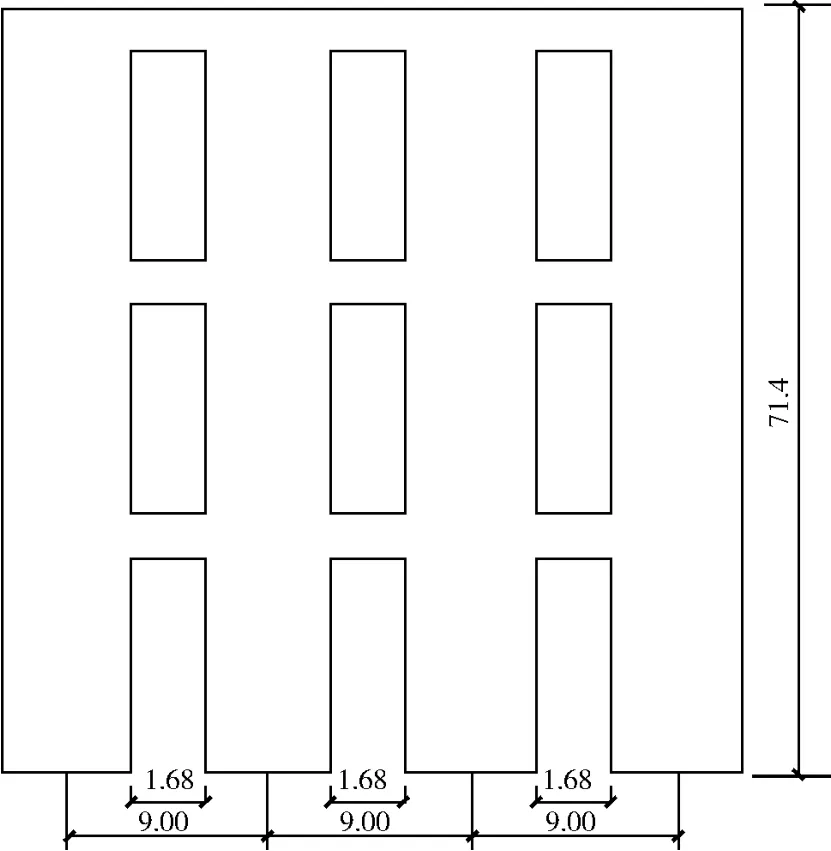
图2 立面图
4 结论
结果表明,考虑连梁作用的多跨短肢剪力墙模型,摒弃了传统欧拉梁模型忽略连梁作用的不足,因而,更接近实际情况。计算结果表明,笔者所得出方法与和Stafford Smith[5]方法的分析结果能够较好地吻合。
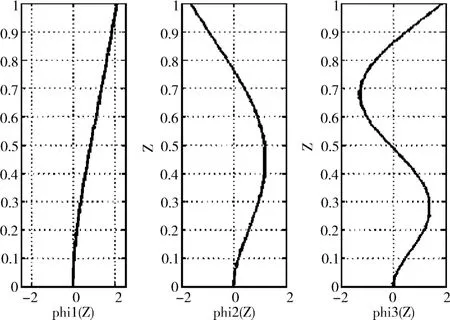
图3 振型图
[1] 黄东升.剪力墙结构的分析与设计[M].中国水利水电出版社,2006
[2] 张晋,吕志波.短肢剪力墙筒体结构模型振动台试验研究[J].东南大学学报(自然科学版),2001,31(6):4-8
[3] 黄东升,程文滚.短肢剪力墙结构动力特性分析的半解析法[J].振动工程学报,2005(9)
[4] 梁启智.高层建筑结构分析与设计[M].广州:华南理工大学出版社,1992:131-133,222-227
[5] Bryan stafford smith,and Young-soo Yoon.Estimating Seismic Base shears of tallwall frame buildings[J].Journal of structural engineering 1991(10)
TU311.3
A
2009-12-17
李创第(1964~),男,教授;陈运凯(1984~),男,研究生;陆运军(1983~),男,研究生。
