多点输入下大跨网壳结构的弹塑性分析
2010-01-15曹现雷白福玉
李 龙,曹现雷,白福玉
(西安建筑科技大学土木学院,陕西西安 710055)
多点输入下大跨网壳结构的弹塑性分析
李 龙,曹现雷,白福玉
(西安建筑科技大学土木学院,陕西西安 710055)
通过对地震动力弹塑性分析原理及方法的介绍,说明对大跨空间结构时程分析时考虑多点输入的必要性。以单层大跨网壳结构为例,利用El-centro地震波研究该结构在8度罕遇地震作用下的变形能力和破坏特征,评价其抗震性能,并提出其在多点输入下弹塑性分析时抗震性能的相关措施及建议,以供网壳工程设计时参考。
大跨网壳; 弹塑性; 多点输入
大跨网壳结构以自重轻、结构刚度好,可以构造中间无支撑的跨度较大的空间,以及丰富多变的优美造型等诸多优点而得到了越来越多的应用。随着计算理论发展和新材料的应用,网壳结构的跨度越来越大,构件厚度越来越薄,结构几何非线性程度提高,其动力特性显著提高,一般的弹性理论分析已经难以满足要求,因此,对此类结构在地震作用下的动力性能研究及相应的设计要求,也得到了众多学者及设计人员的关注[1-3]。根据结构抗震设计指导思想,合理的抗震设计应使结构在罕遇地震作用下部分杆件屈服,材料进入塑性。弹塑性分析是解决结构在罕遇地震作用下延性分析的重要方法之一,因此,对网壳结构动力弹塑性分析的研究十分重要。
本文以单层网壳结构为研究对象,分析了该类结构在地震作用下的动力稳定性能特点,探讨了网壳结构的抗震性能问题,为丰富动力弹塑性分析理论做了有益补充。
1 弹塑性分析原理及方法
多自由度结构体系在地震作用下的动力运动方程为[4]:
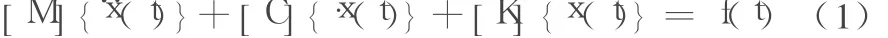
式中:[M]为质量矩阵;[C]为比例阻尼矩阵;[K]为刚度矩阵;{x¨(t)}、{x﹒(t)}、{x(t)}分别为Δt时间步内加速度向量、速度向量和位移向量;f(t)为地面运动向量。Δt时间步内位移、速度与加速度向量增量关系可表示为:
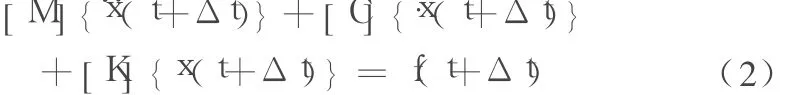
假定在Δt微小时段内加速度{x¨(t)}、速度{x﹒(t)}和位移{x(t)}均为线性变化,则式(1)与式(2)相减得动力方程的增量形式:
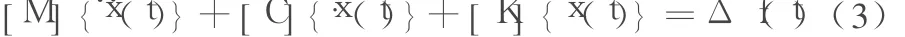
时程分析法就是将简谐力作用时间划分为一系列微小时段 Δt,利用式(3)求解在 0、Δt、2Δt……等各个时刻的近似解。Wilson-θ法由于计算精度高、稳定性好而在时程分析中广泛采用。对运动方程直接积分,从而获得计算系统各质点的位移、速度、加速度和结构构件地震剪力的时程变化曲线。通过计算还可以分析出结构的薄弱层和构件塑性铰位置[5]。因此,这种分析方法能更准确而完整地反映结构在强烈地震作用下的变形特性,是改善结构抗震能力、提高抗震设计水平的一项重要措施。其主要步骤如下:
(1)建立整体结构模型;
(2)定义材料的本构关系,通过对各个构件指定相应的单元类型和材料类型确定结构动力响应的各参数;
(3)定义模型的边界条件;
(4)施加恒、活荷载等竖向荷载值以及风等横向荷载;
(5)在结构构件上定义及分配塑性铰特性值;
(6)输入适合本场地的地震波;
(7)进行弹塑性分析;
(8)分析结构的塑性铰分布、总侧移及层间位移等,综合评估结构的抗震能力。
2 多点输入方法
地震时,从震源释放的能量以地震波的形式传到地表面并引起地面震动,对于平面尺寸较大的结构,由于各支点的距离与地震波的波长在同一数量级,使得地震波到达各支点的时间不同;地球介质的不均匀性,由此产生各支点处地震动的频散损失;各支点的局部土层不同等原因,致使各支点的地震动是不相同的[6],这一点已被许多强震观测记录所证实。
荷载的准确输入是对准确分析大跨网壳结构弹塑性性能十分必要的,多点输入就是在地震动输入中考虑地震动的这种空间变化特性,主要有以下三种实现方法:
(1)先将时间—加速度关系在频域上进行积分,使其成为时间—位移关系,然后施加位移历程载荷。
(2)制定结构的时间—加速度历程,在加速度方向约束地基节点,这时只需要为每一荷载步指定时间和相应的加速度的方向和大小即可。
(3)大质量法。把地基当作很大的质量,由它来带动上部结构的响应。地基节点在激励方向不能约束,只在质量单元上施加适当的力使地基产生所需加速度。此方法的优点是可以得到结构的真实响应位移。
3 地震波的选取
地震波的选择对计算结果的影响较大,不同的地震波分析的结果可能有较大的差别[7]。应使输入的地震波在频谱特征性、有效峰值和持续时间上与工程的实际条件相符。频谱特征性由场地类别和地震分组确定;有效峰值可按规范取值,要使每条记录在统计意义上符合场地特征谱线;持续时间一般为结构基本周期的5~10倍。
对结构地震反应进行时程响应分析所采用的输入地震波,大致可以分成如下三类[8]:(1)拟建场地的实际地震记录;(2)典型的强震记录;(3)人工模拟的加速度时程曲线。由于地震的随机性,所以在同一场地所产生的地震波与过去的实际记录会在很多因素上有很大差异。因此,拟建场地的实际强震记录也不能完全反映今后的实际地震情况。《建筑抗震设计规范》规定:采用时程分析法,应按建筑场地类别和设计地震分组选用不少于二组的实际强震记录和一组人工模拟的加速度时程曲线。
4 实例工程分析
某大跨空间网壳结构,跨度 40m,矢高 8m,单层结构,所有的杆件均为 114.3×4.5的Q235钢管,如图1所示。屋面恒载1.5 kN/m2,活荷载1.5 kN/m2,转化为节点荷载施加在各节点处。本工程选用EL-centro波,考虑行波效应的影响,以及x、y双向输入,特征周期Tg=0.35 s,8度(0.2g),罕遇地震(大震)作用,振动持续时间12 s。
图1 大跨结构图
运用有限元软件对结构进行非线性时程分析[7],采用直接积分法,可以得到结构的塑性铰分布如图2所示,顶点竖向位移如图 3所示,水平位移如图 4所示。可以看出,在地震反应中,基本上所有构件都进入了塑性状态,但是大部分的塑性位于第一阶段,个别杆件达到了第四阶段,部分是第二、第三阶段,最大竖向位移小于跨度的 1/300,满足设计要求。由此可以判断,此工程设计合理,能够承受 8级地震荷载作用,仅需对个别杆件进行优化设计。
5 结束语
本文通过对空间网壳结构动力弹塑性分析,可以得出如下结论:(1)动力弹塑性分析方法可以按照规范对结构的抗震性能作出合理的评价,为实现基于性能的抗震设计提供了很好的计算方法; (2)从弹塑性铰分布情况,可以判断结构薄弱所在;(3)对于大跨网壳结构,结构的弹塑性极限承载力取决于经杆和环杆的刚度和强度;(4)此结构在8度(0.2g)地区,能够满足我国抗震设计三阶段设计标准的要求。
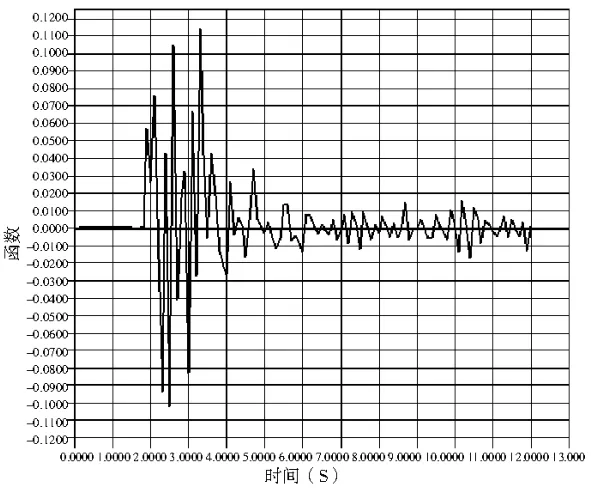
图2 塑性铰分布图
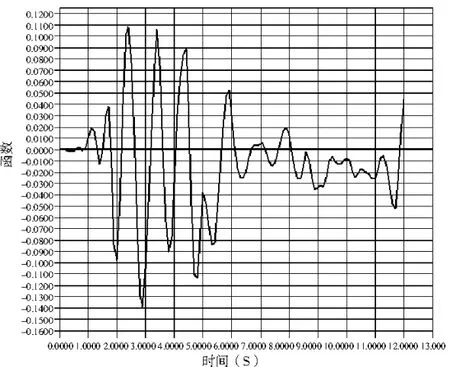
图4 顶点水平位移
[1] 杨飏,支旭东,范峰,等.施威德勒网壳结构的动力强度破坏[J].东北大学学报(自然科学版),2007(1):125-128
[2] 曹正罡,范峰,沈世钊.K 8型单层球面网壳的弹塑性稳定[J].工业建筑,2007(4):69-72
[3] 尧国皇,黄用军,宋宝东.钢框架—钢筋混凝土核心筒结构的动力弹塑性分析[J].深圳土木与建筑,2007(4):56-59
[4] 丁阳,林伟,李忠献.大跨度空间结构多维多点非平稳随机地震反应分析[J].工程力学,2007(3):97-103
[5] 阎晓铭,彪仿俊,陈志强,等.动力弹塑性时程分析方法的二次开发研究[J].深圳土木与建筑,2007(1):18-21
[6] 樊珂.大跨度结构多维多点地震响应试验研究与理论分析[D].北京工业大学,2008
[7] 王旭,邵新刚.钢框架结构地震响应分析研究[J].河北工程大学学报(自然科学版),2009(1):100-101
[8] 孙建梅.多点输入下大跨空间结构抗震性能和分析方法的研究[D].东南大学,2005
TU393.3
A
2010-03-22
李龙(1982~),男,硕士研究生,研究方向为钢结构基本理论;曹现雷(1979~),男,博士研究生,研究方向为钢结构基本理论;白福玉(1985~),男,硕士研究生,研究方向为工程力学。
