数据点云预处理技术研究

齐秀丽

(绥化学院数学与信息科学系,黑龙江绥化 152061)

在逆向工程中,采集实体表面数据是完成实体模型数字化的第一步.数据采集具有多幅性、实物的多样性和数据采集要求的多样性等特点.可根据实体的材质、表面尺寸、表面是否封闭等特征来选择适当的测量仪器和测量方法,进行数据采集.

在逆向工程中,对数据点云的预处理是完成实体模型数字化的第二个步骤.利用测量仪器,可得到关于被测实体表面的大量数据,但是由测量仪器和测量人员都会带来误差,使得所得数据不能全部准确位于被测实体表面;另一方面,因测量设备本身的局限性,所以测量时需要采用多种测量仪对实体表面进行多角度的多次测量,从而使得测得的点云数据不具备序结构.以上这些因素都需要研究者对原始数据点云进行简化、分类聚合和数据配准等预处理.

目前比较经常被采用的方法是:首先,可根据被测实体的表面特征,将其分成不同的部分,使每一部分具有自己的曲面特征 (如初等解析曲面中的平面、球面、柱面、锥面、圆环面,或者为B样条曲面、NURBS曲面,又或者为自由曲面等).这样,数据点云就按照原被测体的几何特征而被分成不同的数据块,对每个数据块进行曲面、曲线重建相对容易.另外,还可对点云作数据配准,把经过多次、多种测量的数据从其自身局部坐标系,通过平移和旋转的方法配准到一个全局坐标系当中.此外,点云中原始数据太多并不利于重建,故需对其进行精简.数据精简的方法主要包括:减少多边形网格中多边形的数量;使用传统的采样方法;使用网格方法.

1 数据配准

采用多种测量仪,对实体表面进行多角度的多次测量,从而使得测得的数据点云不具备序结构,于是需要对原始数据点云做配准处理.比较成功的办法为数据配准的ICP算法.

1.1 两幅距离图像配准到同一坐标系的ICP算法[2]

设两组数据点云是利用数据采集设备从二个视点位置测量实体表面而得到的,这两组数据之间必然有大量重叠区域.首先,从重叠区域中确定几对对应点,对一组数据点云做刚体运动处理,以使得选定的几组对应点之间的距离变小,直到满足收敛条件终止迭代.如果在计算过程中,距离不能在迭代时递减,可以调整对应点的选取方法.已经证明,这个迭代过程可以收敛到局部最小值点;但是,它能否收敛到全局最小值点,则依赖于两幅距离图像的初始位置.根据选择对应点的方法的不同,以及在计算过程中所采用的优化方法的不同.另外,这个方法能够使得最小二乘意义下的距离收敛到局部最小值,但未必能收敛到全局最小值.

1.2 多幅距离图像配准到同一坐标系的ICP算法[2]

如有多幅距离图像,任意选两幅进行配准,可得到一个新的数据点云,然后在其余的里面选择一个与上面得到的新数据点云配准,如此做下去,可得到一幅低精度图像 (数据点云),精度低由误差积累造成的.

1.3 多幅距离图像配准到同一坐标系的改良ICP算法[2]

在多幅距离图像中先选定两幅,首先计算出被测体表面在第一幅距离图像中某给定点处的法线(Chen,Medioni),求出该法线与第二幅距离图像所表示的曲面交点处的切平面,求得第一幅图像选定点在这个切平面上的投影点,与之形成对应,找到所有的对应点即可.这是前面ICP算法1.2的改良方法.

事实上,多幅距离图像中可以任取一幅作为初始图像,将其余图像按上面的改良方法配准到这幅初始图像所在的坐标系中,这次的迭代过程在配准矩阵近乎于单位矩阵的条件下终止.

另外,还有很多非常好的配准方法.如Pulli的渐近式配准法,适用于数据点云十分庞大的情形;还有Turk和Levoy将距离图像的点云连接而将其网格化,得到被测实体表面的网格模型,再将不同幅网格模型相互配准而成一幅具有几何特征的实体的网格表示.这些虽然在速度和准确性上占有优势,但是在保留图像特征方面也有不尽人意之处,而且在解决曲面拼接、求交、延拓和过渡等问题时的效果也不够理想.

相对来说,视点云为无序散乱点云而进行配准,再利用配准后的点云重建曲面,所得曲面能极大的与原测量实体表面保持拓扑一致.

2 数据整合与优化

随着三维扫描技术的发展,能够十分容易的获得包含大量数据的点云.但由于误差的存在,又由于没有必要的直接用海量的原始数据点云进行曲线曲面重建,所以需要对于数据点云进行整合.数据整合的方法主要包括以下几类[1]:

(1)基于雕刻的方法.相比之下,人们更愿意将数据点云处理成多边形网格模型,因为其具有形状简单、容易处理、能够以任意精度逼近任一曲面等特点,而且易被分割成三角形,所以人们首先将点云Belaunay三角化,然后按照规则找出与目标一致的三角面片,从而得到三角形网格模型,如Boissonnat的方法,Crust算法,基于α-Shape的方法等等.

(2)跟踪等值线的方法.如Happe提出的算法.

(3)基于细分空间的方法.如数据处理中比较传统的包围盒法.

(4)区域增长的方法.先构造一个种子三角面片,将其三边加入活动链表进行处理,对每一条活动边,按某规则在点云中为其寻找新点与之构成三角形,以新产生的边替代原活动边,将其加入链表,继续寻找新点.这种方法往往需要借助于事先确定的参数,这种人为的因素对算法的可靠性有很大的影响.

为了使从点云重建得到的三角网格曲面能够进行正确的后继处理,在CAD中得到实际应用,必须保证这个重建出来的网格曲面是拓扑正确的,即重建曲面与被采样物体表面是拓扑同胚的.Amenta和Bern、Petitjean和Boyer Adamy,Giesen和John用不同的思路对此进行了研究,也有很好的算法产生.但是,如果重建曲面与被采样物体表面的拓扑结构差别较大,则会衍生出运算量很大的线性规划问题,有时甚至无解.

3 面对散乱数据点集,基于数学期望的数据点云预处理

3.1 设{Pi|i=1,2,…}为原始数据点集.将其投影到一个网格平面上.含有数据点的网格点则称为黑点,所有的黑点构成平面区域记为Ω.

定义1 平面上两个网格点 P(i,j),Q(m,n)的距离 d(P,Q)=|i-m|+|j-n|.

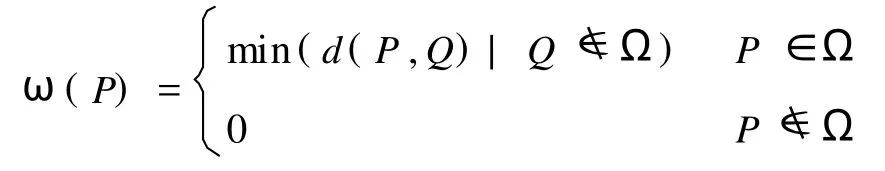
3.2 在ω的每一个网格黑点中,进行数据简化.

定义3 设随机变量ξ的所有可能取值为mj,1≤j≤t.

定义4 设随机变量η的所有可能取值为nj,1≤j≤t,

分别计算这两个随机变量的数学期望 Eξ和Eη[3],记 m=Eξ,n=Eη.取初始点为 Q0(m,n).

对于当前网格内的数据点 P,若|PQ0|>λ,则去除该点;若|PQ0|≤λ,则保留该数据点.

对Ω内的每一个网格点,作如上处理,可以精简数据点,而且保留了数据密集处的数据点.

3.3 根据网格点权值的定义,选出适当的网格点为初始点 Q′0.

对于权值最大的点 Q0,以其为心,以(P)为半径 ,作邻域 N°(Q0,(P)),考察该邻域内的所有数据点{Pi|i=1,2,…,t},记数据点 Pi的坐标为(mi,ni).

按照3.2讨论随机变量ξ、η,分别计算这两个随机变量的数学期望 Eξ和 Eη,记 m=Eξ,n=Eη.取初始点为 Q′0(m,n).

3.4 按照参考文献[1]的方法选择方向,建立点 Q′0处的局部坐标系,对于当前点 Qk,作以 Qk为圆心,以r为半径的圆,在圆内考察与 U的夹角小于90°的数据点Pi(即为圆内的点).规定θi为两个特殊方向的夹角.取 I1和 I2,加入调节因子η,而构造 I1+ηI2.要选取适合k,而使得 I1+ηI2=min,从而确定出方向,选取下一个点 Qk+1.

在当前点满足 d(Qk-1,Qk)>2,或者时,则终止过程.

如上,可建立起一个点列{Qk},即为预处理之后的数据点云.该点云已将分布较稀疏部分的数据点精简掉,并按照数学期望意义下数据密集的位置对点云进行了预处理.

[1]钟纲,杨勋年,汪国昭.平面无序点集曲线重建的跟踪算法 [J].软件学报,2002,13(11):2188-2193.

[2]Besl P.J and McKay N.D.A method for registration of 3D shapes.IEEE Transactions on Pattern Analysis and Machine Intelligence,VOL(14),No.(2),239-256,1992.

[3]魏宗舒,等.概率论与数理统计教程 [Z].北京:高等教育出版社,2000.