关于图 C3∪P3n的优美性
2010-01-15吴跃生毛国珍
吴跃生, 毛国珍
(1.华东交通大学基础科学学院,江西南昌 330013; 2.江西赣州市第三中学, 江西赣州 340001)
1 引言与概念
本文所讨论的图均为无向简单图,V(G)和 E(G)分别表示图 G的顶点集和边集,未说明的符号及术语均同文[1].
定义1[2]在含有 n个顶点的路Pn上,当且仅当两点的距离为3时增加一条边,所得到的图叫做 P3n.
图P3n的优美性[2-7]是众多学者研究的对象.本文研究不交并图 C3∪P3n的优美性.
定义2[1]对于一个图 G=(V,E),如果存在一个单射θ:V(G)→{0,1,2,…,|E(G)|}使得对所有边e=(u,v)∈E(G),由θ′(e)=|θ(u)-θ(v)|导出的 E(G)→{1,2,…,|E(G)|}是一个双射,则称 G是优美图,θ是G的一组优美标号,称θ′为G的边上的由θ导出的诱导值.
2 主要结果及其证明
定理1 当 n≥4时,C3∪P3n是优美图.
证明:当 n≥4时,设图 C3∪P3n的顶点集如图1所示.
下面给出图 C3∪P3n的标号θ:
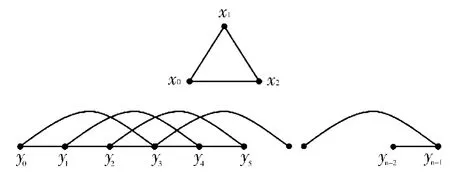
图1
(1)当n=6k时,
θ(x0)=1,θ(x1)=4,θ(x2)=3
θ(y6j)=7j,θ(y6j+1)=12k-5j-1,
θ(y6j+2)=7j+2,
θ(y6j+3)=12k-5j-2,
θ(y6j+4)=7j+5,θ(y6j+5)=12k-5j-3,其中 j=0,1,2,…,k-1
(2)当n=6k+1时,
θ(x0)=1,θ(x1)=4,θ(x2)=3
θ(y6j)=7j,其中 j=0,1,2,…,k,θ(y6j+1)=12k-5j+1,θ(y6j+2)=7j+2,
θ(y6j+3)=12k-5j,θ(y6j+4)=7j+5,θ(y6j+5)=12k-5j-1,其中 j=0,1,2,…,k-1,
(3)当n=6k+2时,
θ(x0)=5,θ(x1)=7,θ(x2)=8
θ(y0)=0,θ(y1)=12k+3,θ(y6j+2)=7j+2,θ(y3)=12k+2,θ(y6j+4)=7j+4,θ(y6j+5)=12k-5j-1,θ(y6j+6)=7j+6,θ(y6j+7)=12k-5j-2,其中 j=0,1,2,…,k-1
θ(y6j+9)=12k-5j-3,其中 j=0,1,2,…,k-2
(4)当n=6k+3时,
θ(x0)=1,θ(x1)=4,θ(x2)=3
θ(y0)=0,θ(y1)=12k+5,θ(y2)=2,θ(y6j+3)=12k-5j+4,θ(y6j+4)=7j+5,
θ(y6j+5)=12k-5j+3,θ(y6j+6)=7j+8,θ(y6j+7)=12k-5j+2,θ(y6j+8)=7j+10,
其中 j=0,1,2,…,k-1
(5)当n=6k+4时,
θ(x0)=5,θ(x1)=7,θ(x2)=8
θ(y0)=0,θ(y1)=12k+7,θ(y6j+2)=7j+2,θ(y3)=12k+6,其中 j=0,1,2,…k,
θ(y6j+4)=7j+4,θ(y6j+5)=12k-5j+3,θ(y6j+6)=7j+6,θ(y6j+7)=12k-5j+2,θ(y6j+9)=12k-5j+1,其中 j=0,1,2,…,k-1.
(6)当n=6k+5时,
θ(x0)=5,θ(x1)=7,θ(x2)=8
θ(y0)=0,θ(y1)=12k+9,θ(y6j+2)=7j+2,θ(y3)=12k+8,
θ(y6j+4)=7j+4,其中 j=0,1,2,…,k,θ(y6j+5)=12k-5j+5,θ(y6j+6)=7j+6,
θ(y6j+7)=12k-5j+4,θ(y6j+9)=12k-5j+3,其中 j=0,1,2,…,k-1.
只对 n=6k的情况给予证明,其余类似可证.
上面的标号,对yj(j=0,1,2,…6k-1)来说,每个偶数顶点的标号是从小到大排列,最大的标号是7k-2;每个奇数顶点的标号是从大到小排列,最小的标号是7k+2;又θ(xi)≠θ(yj)(i=0,1,2;j=0,1,2,…6k-1).因此,存在一个单射由θ′(e)=|θ(u)-θ(v)|导出的为双射;所以θ是的优美标号.
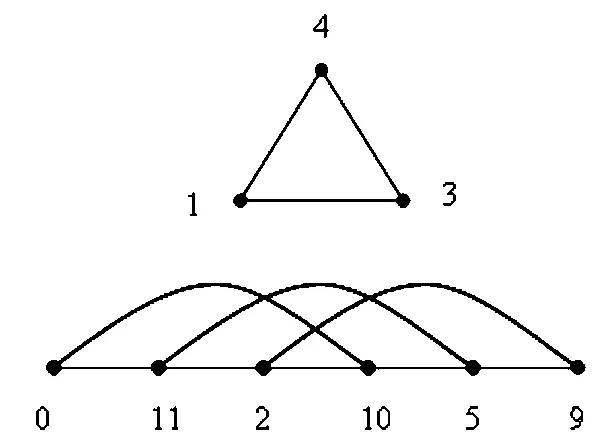
图2

图3

图4
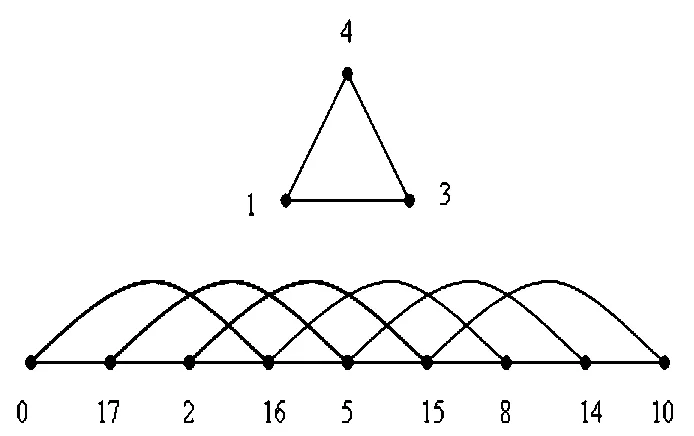
图5
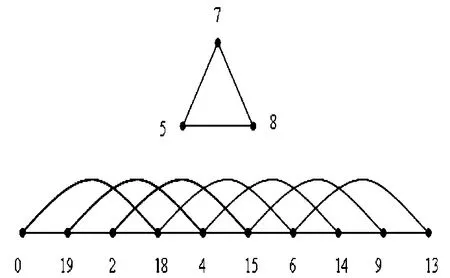
图6
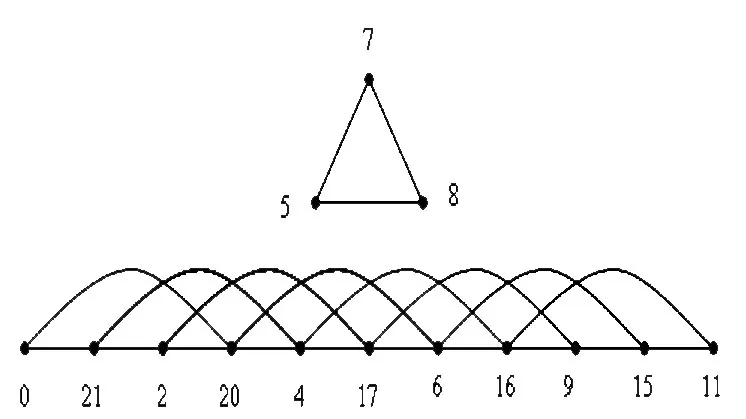
图7
[1]马杰克.优美图 [M].北京:北京大学出版社,1991.
[2]林育青.关于图 P3n的优美性 [J].华南师范大学学报 (自然科学版),2000,(3):21-24.
[3]严谦泰,李武装.关于图 P3n优美性的研究 [J].数学的实践与认识,2005,(4):131-139.
[4]王云,张秉儒.论图 P3n的优美性 [J].电脑知识与技术,2007,(6):1661-1664.
[5]邓怀敏,林育青.图 P3n的优美标号 [J].新疆大学学报 (自然科学版),2000,(2):12-16.
[6]付明彦,刘小冬,王力工.再论图 P3n的优美性 [J].西南民族大学学报自然科学版,2007,(3):456-459.
[7]严谦泰.张忠辅,关于 P3n的优美性 [[J].数学研究与评论.2004,24(2):89-92.
